连梁梁端埋入长度计算

（1）求解Cb和Cf

①基本假定

为了确定预制连梁与墙肢在连接界面处的应力和应变分布，进而计算其约束弯矩，须做如下假定：

图4.16 连梁埋入部分受力简图

a）FRC受压本构关系取为：

式中，σu为极限压应力；ε0为起裂压应变；εu为极限压应变。

b）根据变形协调原理，弹性模量大的部分刚度大，变形小。因此，假设弹性模量小的构件发生变形。本文连梁FRC弹性模量小于墙肢中普通混凝土的弹性模量，因此认为连梁达到其承载能力极限状态时，梁端处RFC首先达到极限压应变，即连梁B端FRC达到极限压应变εu。

c）假设预制连梁与墙肢在连接界面处的变形协调，并呈线性分布。连梁B端处的材料达到极限压应变εu，相应地A端处的材料应变为εb，如图4.17所示。图4.17中xb及xf分别为连梁埋入部分中性轴至连梁端部A及连梁与墙肢交界面B的距离。

②积分求解Cb和Cf

根据以上假定，连梁埋入端块受压区BC段压应力的合力为：

图4.17 求解Cb和Cf时假定的应力、应变分布图

将代入上式中，得

AC段压应力的合力Cb为：

将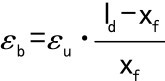代入上式中，得

压应力合力Cb合力作用点及压应力合力Cf合力作用点至中和轴的距离分别为：

（2）求解Nt和Nc

①基本假定

图4.18（a）为连梁在力矩作用下沿连梁轴力方向锚固部分的受力简图。假设连梁达到极限锚固长度时，在力矩作用下梁端A压应变εc=0，梁端B压应变εc=εu，且AB段压应力σc呈三角形分布，如图5.18（b）所示，AB段拉力Nt=Nc。

图4.18 求解Nt和Nc时假定的应力分布图

②求解Nc

根据以上假定，连梁埋入部分B端应变为εu，将其代入式（4-51）中，得B端的压应力σB为：

σB=σu（4-58）

根据假定的Nc沿AB方向的应力分布图，可知：

（3）建立平衡方程求解ld

根据竖向力的平衡条件，可得

Vu=Cf-Cb（4-60）

将式（4-53）和式（4-55）代入式（4-60），得

同理，根据力矩平衡条件，可得

将式（4-53），（4-55），（4-56），（4-57），（4-59）代入式（4-62）中，得

式（4-61）和式（4-63）中，将σu取为FRC轴心抗压强度，即σu=fc，令εu=0.33%，ε0=0.2%，则

由方程组（4-64）可得：

式中，ld为连梁梁端埋入长度；ln为连梁净跨；Vu为连梁受剪承载力；b为连梁截面宽度；h为连梁截面高度；fc为FRC轴心抗压强度。

由式（4-65）可知，连梁梁端埋入长度ld的大小主要取决于剪压比Vu/（fcbh0）（h0为连梁截面有效高度，取为0.9h）、跨高比ln/h和连梁截面高度h的大小。连梁梁端埋入长度随剪压比Vu/（fcbh0）、跨高比ln/h、梁截面高度h的增大均呈非线性增加。

跨高比不大于2.5的FRC对角斜筋小跨高比预制连梁以受剪为主，最终发生剪切破坏，连梁剪力按实际受剪承载力计算，即

Vu=Vwb（4-66）

对于弯曲破坏的预制混凝土连梁（无对角斜筋），连梁剪力取连梁受弯屈服时对应的剪力值，即