【摘要】:由式可知,改变比值R2/R1,可以改变二阶系统的阻尼比ξ,改变RC值可以改变无阻尼自然频率nω。工程上把阻尼比ξ=0.707的二阶系统称为二阶最优系统。ξ≥1,响应与一阶系统相似,没有超调,但调节速度慢,进入稳态需要较长时间,二阶系统单位阶跃响应曲线如图3-11所示。通过仿真实验,学生在具体实验箱操作时,可以分别选择R2=0 kΩ,140 kΩ,200 kΩ和400 kΩ进行实际实验操作。这样可以更好地实现“理论指导实践,实践反映理论”的目的。
二阶系统的模拟电路图,如图3-7所示。
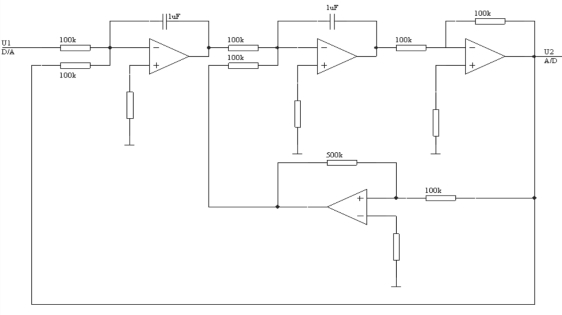
图3-7 二阶系统的模拟电路
系统的闭环传递函数为:
![]()
典型二阶系统的闭环传递函数为:
![]()
比较式(1),式(2),可得:
![]()
由式(3)可知,改变比值R2/R1,可以改变二阶系统的阻尼比ξ,改变RC值可以改变无阻尼自然频率nω。
二阶系统电路的结构如图3-8所示。

图3-8 二阶系统电路的结构图
仿真分析
利用Simulink建立仿真框图如图3-9所示。

图3-9 二阶系统仿真框图
或者表示为如图3-10所示。
根据阻尼比ξ在不同的范围内取值,二阶系统的单位阶跃响应对应的运动规律如下:

图3-10 二阶系统Simulink仿真框图
(1)ξ<0,响应发散,系统不能正常工作。
(2)ξ=0,系统以最快的速度进入稳态,但响应曲线是等幅振荡的。
(3)0<ξ<1,虽然响应有超调,但是上升速度比较快,调节时间比较短。工程上把阻尼比ξ=0.707的二阶系统称为二阶最优系统。
(4)ξ≥1,响应与一阶系统相似,没有超调,但调节速度慢,进入稳态需要较长时间,二阶系统单位阶跃响应曲线如图3-11所示。其中,

图3-11 二阶系统单位阶跃响应曲线图
ξ <0 对应的是(R2/R1)<0,这在实际中是无法实现的,因为实际中的电阻值为正,通过Simulink 仿真可以解决这一问题。通过仿
真实验,学生在具体实验箱操作时,可以分别选择R2=0 kΩ,140 kΩ,200 kΩ和400 kΩ进行实际实验操作。这样可以更好地实现“理论指导实践,实践反映理论”的目的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















