正规光波导

介质折射率沿纵向不变的光波导称为正规光波导，也就是说，在正规光波导中，ε＝ε（x，y）。正规光波导是最典型的光波导。

1.模式的概念

用分离变量法可以证明Helmhotz方程（3.1.13）和方程（3.1.14）

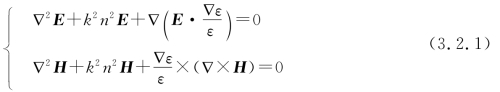
有形如

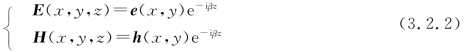
的解，β＝β（ω，ε）称为纵向传输因子，振幅e（x，y）和h（x，y）描述光场沿波导横截面的分布。注意，e（x，y）和h（x，y）是横坐标的函数，但其方向并不限于横截面内。令

连同式（3.2.2）代入式（3.2.1），得

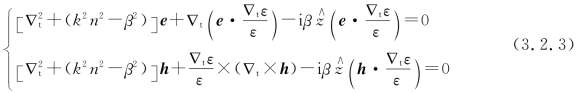
这是两个二元偏微分方程，其中，在推导式（3.2.3）的第二式时用到了式子

根据偏微分方程理论，在边界条件给定时，式（3.2.3）有无穷多个离散的可排序的特征解，每个特征解可表示为

称为一个模式。一个模式是正规光波导中可存在的光场沿横截面分布的一种图形。这种图形沿正规光波导的纵向不变。表征一个模式的基本物理量是它的纵向传输因子β。若β为实数，光场在传输中只有相移而无衰减；若β为复数，光场在传输中既有相移又有衰减。光波导中的总光场是所有可存在模式的线性叠加。

2.模式的纵向分量和横向分量的关系

令：

代入式（3.1.16），得

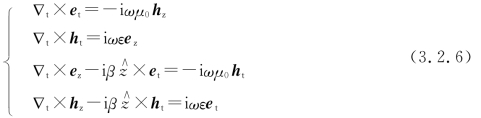
利用∇t×e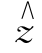＝－×∇tez。可将式（3.2.6）第三、第四式改写为

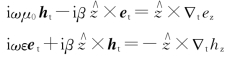
联立上两式，注意到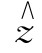×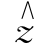（×et）＝－et，得

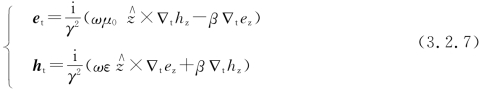
这说明模式场的横向分量可由纵向分量唯一确定，其中的称为横向传播常数，它一般不等于零，如图3.2.1所示。

同理，若将式（3.2.5）代入Maxwell方程组（3.1.10）后两式，可得

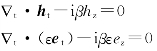
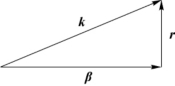
图3.2.1　k，p，r三者的矢量关系

也就是

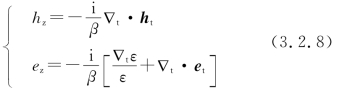
这说明模式场的纵向分量可由横向分量唯一确定。

下面讨论模式场分量的相位关系。将坡印廷矢量在柱坐标中分解为

其中的分量分别是

由于模式在正规波导中传输时，能量沿纵向传输，故纵向分量Sz一定是实矢量，两个横向分量都是虚矢量。因此，eφ与hr，er与hφ同相，而ez与hr，er与hz，ez与hφ，eφ与hz有的相位差。