开普勒和地球

公元1601年深秋的一天，这是哥白尼去世后的第28年，30岁的开普勒正急匆匆地赶往他的老师第谷的家中。据下人来报，第谷突发急病，可能要不行了，他点名要见开普勒，似乎有什么极为重大的事情要交代给开普勒。

55岁的第谷奄奄一息地躺在床上，脸色蜡黄，眼神迷离，他有一副特别浓密醒目的八字胡，修剪得很有型，鼻梁看上去显得坚硬粗大，泛着金属的色泽，与整张脸似乎不大协调。当看到开普勒终于来到卧榻边时，第谷松了一口气，自己还没咽气，太好了！

开普勒忧虑地问：“老师，你怎么了？昨天还好好的，怎么突然一下就……”说着，已经泣不成声。

第谷伸出手摆了一下，示意开普勒别哭，听他说话，开普勒强忍住抽泣，注视着第谷。

第谷缓缓地说道：“我这辈子干了不少荒唐的事情。”他指了指自己的鼻子，努力装出笑容，“但总算也做了一些有意义的事情，此生算是没有虚度。”

开普勒使劲点了点头：“老师，你已经为天文学做出了巨大的贡献，毫无疑问你是这个时代最杰出的天文学家。”

第谷摆手示意开普勒停住，听他说话。

“我此生最大的遗憾就是没有完成我的行星运动理论，托勒密和哥白尼都错了，我才是对的，只是我恐怕来不及完成所有的公式了。开普勒，只有你能继承我的遗志，完成我的理论，那些我视若生命的观测数据现在全都交给你了。原谅我过去一直不肯给你看这些资料，我的心胸太狭小了，我怕你抢先完成正确的行星运动理论啊！因为我知道你的天赋比我好多了，数学能力更是无人能及。我坚信，这批宝贵的、独一无二的资料交到你的手里，你一定能用它们创造出奇迹来。”

听到这里，开普勒是又惊又喜。他师从第谷这两年多来，一直无法看到所有的资料，老师总是像挤牙膏一样地一点点给，还专门让自己立下绝不泄密的字据，可见第谷是多么珍视自己的这批数据资料。现在他居然要把所有资料全部留给自己，这让开普勒激动不已。

开普勒含着泪水，点头答应着：“老师你放心吧，我一定完成你的遗愿。”

那天晚上，第谷安详地离开了人世，他把自己毕生心血凝结成的几大麻袋资料都交给了开普勒。那么，第谷到底是什么人？他的资料又为何如此珍贵呢？

第谷出生于一个丹麦的贵族家庭，从小就不愁吃不愁穿。他很小就迷上了天文学，到30岁时，他已经成为丹麦王国中名气最响的天文学家。恰好当时的丹麦国王也是一个天文迷，他赐给第谷一个岛，叫汶岛（今天该岛在瑞典境内），并且拨了一大笔钱给第谷。第谷用这笔钱在汶岛上造了两座豪华雄伟的天文台，一座叫天堡，一座叫星堡，并且雇佣了40多个助手。第谷是一个天文测量仪器的设计制造大师，他设计并制造了一批可能是当时世界上最大、最先进的天文测量仪器。

图6-1　整面墙就是一个象限仪（左）

大型六分仪（中）

大型象限仪（右）

第谷这个人性格偏执，脾气古怪。他年轻的时候，因为跟人争论谁是世界上最好的数学家，居然去决斗，结果命是没丢，鼻子却丢了，整个被削掉，于是他给自己做了一个金属假鼻子贴在脸上，倒也几可乱真。正是这样一个偏执狂才能在小岛上一住就是21年，要不是国王驾崩，他失去了经济来源，估计会终生在岛上观测星星。第谷的鼻子不好，但是视力却出奇地好。那个年代，望远镜还没有发明出来，所有的观测都是用裸眼进行的，这在今天看来，简直不可思议。根据后人的研究，第谷测得的天体位置误差已经小于2角秒，这几乎是肉眼所能达到的精度极限。21年如一日的观测，让第谷拥有当时世上最齐全，精度最高，时间跨度最长的恒星和行星观测数据，第谷将它们视为生命。然而一个人有所长，就有所短，第谷是观测上的巨人，却是理论计算上的矮子，他对数据的敏感度很差，数学能力也很一般。他不喜欢哥白尼的学说，因为哥白尼把地球说成是一颗普通的行星，这在感情上，他无论如何也接受不了。而且他觉得托勒密的学说太丑了，弄出那么多的轮子，计算值还与观测值差别那么大，在第谷这样一个观测大师眼里，也是绝不能容忍的。那怎么办呢？第谷冥思苦想，终于想出了一套自己的理论，那就是地球是宇宙的中心这条不动，五大行星绕着太阳转，太阳又带着这五大行星绕着地球转，这哥们把托勒密和哥白尼折中了一下，凑出了自己的理论，亏他想得出，还对此深信不疑呢！

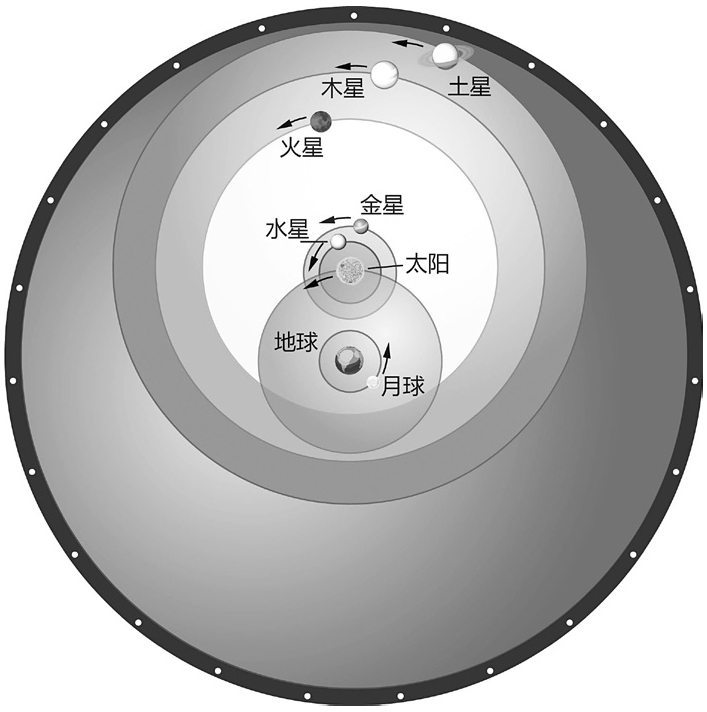
图6-2　第谷的宇宙模型

但问题是，模型是凑出来了，接下去的数学定量论证却怎么也搞不定。后来机缘巧合认识了开普勒，第谷马上意识到这个年轻人是数学奇才，能补自己的短，于是认了开普勒这个学生。其实明面上是学生，私下里第谷把开普勒当作自己的救星，他希望开普勒帮助自己完成艰深复杂的数学论证。

第谷不知道的是，开普勒其实是哥白尼的忠实拥护者，只是碍于面子，他从来没有告诉过自己。现在，第谷过世了，开普勒得到了那批珍贵的数据资料，宝剑终于到了英雄的手里，奇迹就要发生了。

开普勒是典型的苦孩子出生，家境贫寒，但如同大多数文艺作品中的励志故事一样，穷苦的开普勒一路靠着奖学金念到大学毕业。他是个数学奇才，脑子非常好使。与哥白尼颇有相似之处的是，他大学的专业是神学，却痴迷于天文学。不过，上帝似乎有意刁难这个苦孩子，喜爱天文的他居然视力极为糟糕，而且年龄越大越糟糕，所以，高度近视的开普勒与天文观测基本无缘了。但恰恰是这个弱点成就了开普勒的传奇，正因为他无需整夜整夜地趴在楼顶上看星星（其实不是不想，确实是心有余而力不足），使他获得了整夜整夜趴在书桌上算来算去的时间。别人用眼睛来研究天上的星星，开普勒却只需要别人的观测记录，再加上纸和笔，就足够了。

当开普勒拿到他老师第谷的宝贵资料时，刚好30岁整。接下去的8年，他全力以赴地投入到对火星的研究中。期间第谷的女婿跑出来抢跑了第谷的资料，开普勒又设法要了回来，来回这么折腾了几年，开普勒的热情始终没有减退。他夜以继日地画啊，算啊，终于在1609年迎来了首次突破，行星运动规律的秘密被开普勒揭示了出来，人类得以第一次真正意义上窥视到了宇宙的奥义。

接下去这段我会用图文的方式讲解开普勒的思考和计算过程，可能会有点儿枯燥，如果你对几何和数学没太多好感的话，我建议你直接跳过下面一整段，不要紧。但如果你对数学不那么厌恶的话，也可以看一下，你会感受到那种揭秘的乐趣。

由于火星运动时，地球也在运动，所以为了求得火星的运行轨道，必须先确定地球的运动轨道。开普勒先假定，相对于地球而言，地球和火星的运行轨道都是偏心圆，然后在各个相继到来的火星年，也就是当火星每年回到原来的位置时来确定地球的位置。我们用下面这张图来说明开普勒的计算过程：

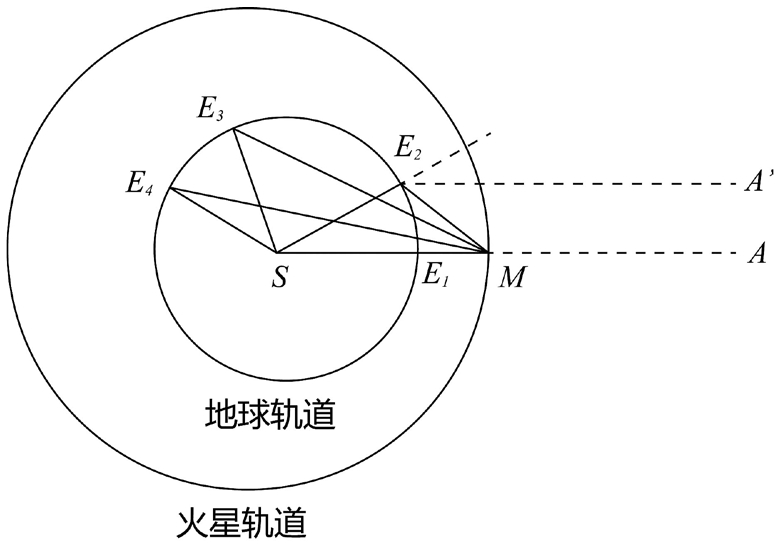
图6-3　由火星观测资料定出地球的轨道

火星M，地球E1，太阳S在一条直线上，此时从地球E1看火星M时的星空位置为A。一个火星年后，火星重新回到M点，地球来到E2点，在三角形E2SM中，∠SE2M是经过一个火星年后从地球看太阳和火星间的张角，它可以由第谷留下的观测资料定出。∠S2EM=180°－∠SE2A＇，此处E2A＇和MA相平行，它交于天穹上的同一点，所以∠SE2A＇乃是经过一个火星年后从地球看太阳和星空位置A之间的张角，它也可以由第谷的观测资料定出。这样∠E2SM也就能求出。于是，若以基线SM为长度单位，从三角形E2SM便可以求得SE2。2个火星年后，地球到了E3处；三个火星年后地球到了E4处……用上述类似的方法同样可以求出SE3，SE4……于是他定出了地球的偏心圆轨道。

地球的轨道确定后，开普勒又进一步考虑地球在轨道上的运动速度有何变化。他恢复了托勒密首创而被哥白尼否定的均衡点概念，但他引入均衡点仅仅作为一种数学技巧，而且太阳与均衡点相对于地球圆轨道中心的距离不再相等。如下图：

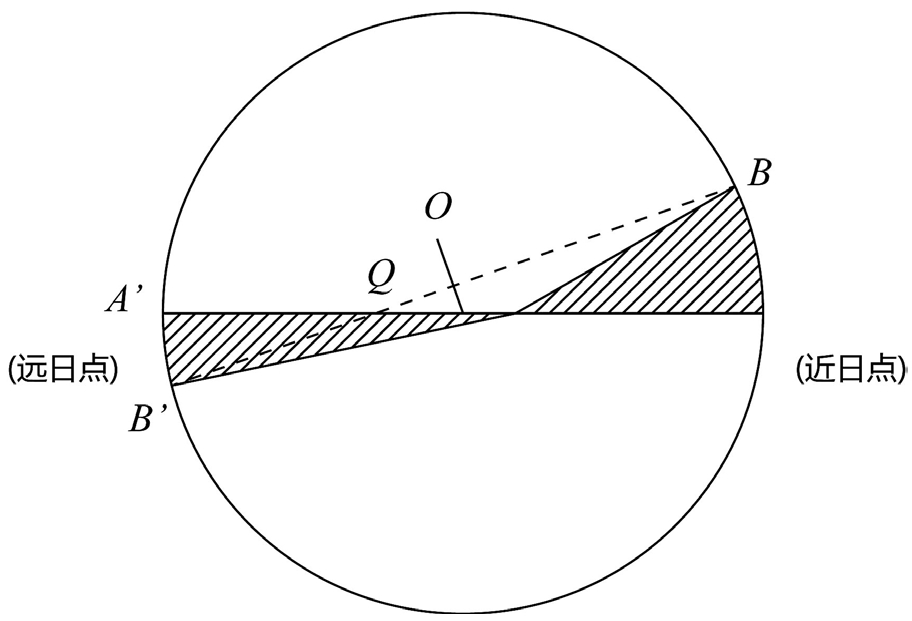
图6-4　在地球绕太阳轨道是偏心圆的假定下，开普勒推出面积定律

若地球在以O为中心的圆轨道上运动，S为太阳，Q为均衡点，AB弧和A＇B＇弧分别为相同时间里地球在轨道上近日点附近和远日点附近所走过的弧段。按照均衡点的定义，∠AQB=∠A＇QB＇，因此，显然∠ASB大于∠A＇SB＇，但它们之间有什么定量关系呢？开普勒根据第谷留下的大量观测资料来凑算，最后获得的结果是图中扇形ASB和扇形A＇SB＇的面积应该相等。这一结果可以表达为：在相同的时间里，地球到太阳的连线扫过的面积相等。这一结论的推广便是行星运动的第二定律，或称为面积定律。

就这样，开普勒发现了行星运动的奥秘，在1609年，他出版了《新天文学》一书。八年的艰辛求索，最后凝结成两个简洁无比的定律：

开普勒第一定律

行星绕日运行轨道是一个椭圆，太阳位于其中的一个焦点上。

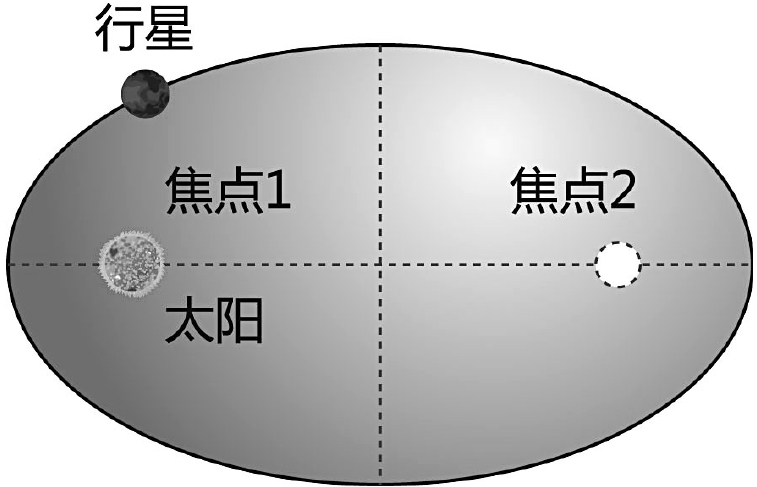
图6-5

开普勒第二定律

在相同的时间内，行星到太阳的连线扫过的面积相等。

图6-6

无论用什么样的词汇来赞美开普勒的这两个伟大发现都不为过，这是人类第一次触摸到了“上帝”的意志。开普勒以一人之力，首次揭示出行星与太阳之间如此隐密的数学联系，他当然可以称得上是人类的英雄。

有了开普勒的这两个定律之后，仅仅只需要用7个椭圆（金、木、水、火、土、地球、月亮的运动轨道）就足以取代哥白尼的34个轮子，并且计算起来，不但简洁明了，精度也进一步提高，这才是真正的宇宙和谐之美啊。

此时的开普勒刚刚年满38岁，正当壮年，他当然不会就此停止探索的脚步。在他还是20多岁时，就坚信行星到太阳的距离之间一定存在某种神秘的联系，上帝肯定不会随意摆放它们的位置。他当时有一个奇思妙想，说世界上只有五种正多面体（正四面体、正六面体、正八面体、正十二面体和正二十面体），而天上刚好也只有五颗行星，这必然不是巧合，上帝一定是按照正多面体的方式来挨个安排五大行星的位置的。当然，开普勒很快就抛弃了这种硬凑的想法，但是他依然坚信行星的位置有规律可循，绝不是随意的。他又踏上了新的求索之路，这一走就是整整10年。

开普勒是学术上的幸运儿，却是生活中的苦命儿，在38岁到48岁的这10年间，悲剧屡屡降临到他的头上。先是工作单位总是发不出工资，然后又丢了工作，家里揭不开锅，接着儿子和妻子相继病逝，完了又是被迫迁徙、再婚。一连串的生活变故接踵而至，让开普勒疲于奔命，但他心中那团天文学的热情之火却从未熄灭。一有时间，他就会拿起纸笔，开始演算。在遭受了不计其数的失败之后，皇天终于不负有心人，1619年，行星运动的第三个定律被开普勒奇迹般地发现。说它是奇迹，在我看来一点儿都不夸张，因为第一和第二定律看上去并不是怎么惊世骇俗，还是比较直观的，但这个第三定律却不一样，它的内容足以让人大为惊诧。我真是忍不住惊叹，开普勒到底是怎么发现它的？从成千上万的数据中找出这样的一个规律，除了需要勤奋之外，绝对还需要一些神奇的第六感之类的天赋。让我们来看看第三定律的内容：

行星绕太阳公转周期的平方与轨道椭圆长半轴的立方成正比。（注意，这里面的公转周期是一个时间单位，而长半轴则是一个距离单位。）

再讲得通俗一点，就是行星绕太阳转一圈的时间各不相同，有长有短，但是这些时间之间的数值比例与它们到太阳的距离有映射关系。这些关系式中又是有平方，又是有立方的，并不直观，但居然就被开普勒给发现了。我觉得这实在是太牛了，越想越觉得真不可思议。有人可能要问：这第三定律有什么用呢？或许聪明的读者已经发现，对于预测天象来说，有第一、第二定律就已经足够了，这第三定律能干吗呢？大有用处！它能计算出行星离我们有多远。我们来举个例子，现在假设地球到太阳的距离是一个天文单位，用1AU来表示，我们又知道地球绕太阳一周是一年，现在，通过观测火星的位置，我们可以得出火星绕太阳一圈需要687天，不到2年，但为了便于打比方，我们权当就是2年吧。那么根据开普勒第三定律，火星公转周期的平方与地球公转周期的平方之比，等于两星到太阳距离的立方之比。假设火星到太阳的距离是X，那么方程式就很简单了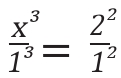：。于是，我们可以得到x3=4,接着可以算出x=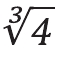≈1.59(AU)，结果就是火星到太阳的距离是地球到太阳距离的约1.59倍。用同样的方法，五大行星的距离就全都可以知道了。再进一步知道这些距离后，当时的人们就认为可以估算宇宙的大小了。你想，连宇宙的大小都可能推算出来，那这个用处已经大到不能再大。不过呢，你可能看出来了，这里面还需要一个关键的数据，就是日地距离，也就是1AU（一个天文单位）到底是多长。如果不知道这个数据，那么一切都白搭。一旦把这个数据搞清楚，那么宇宙就没有秘密了，至少当时的人们是这么认为的。因此，在此后的几百年间，1天文单位的值成了天文学第一问题，一代又一代的天文学家为攻破这个问题，呕心沥血，前赴后继，甚至丢掉性命。这是后话，你听我讲下去就会知道了。

开普勒在1619年出版的《天体和谐》一书中正式公布了他的第三定律，他在书中写下这样的文字：大功终于告成了！或许我要等上一个世纪才会有读者，但这有什么关系呢，上帝不也是等了6000年才有信仰者吗？

开普勒没料到的是，他很快就有了大批拥护者，毕竟实践是检验真理的唯一标准嘛！开普勒后来用他的三定律演算而编制的《鲁道夫星表》，误差不到10角秒，在此后的150年中，它都是世界上最好的星表。开普勒之后，哥白尼的日心说逐渐正式登上了大学课堂，真理开始冲破教会的权威，在学术圈广为传播。但是追求真理的征程只是刚刚开了个头，依然有两个重要的问题摆在所有理性的人们面前：第一，太阳是宇宙中心的证据在哪里？从哥白尼到开普勒，他们的理论到底只是一种数学技巧还是客观真相？《圣经》真的错了吗？光是讲道理不行，科学需要的是证据。

第二，为什么行星的轨道是一个椭圆？为什么公转周期与距离有种神秘的数学关系？科学精神驱动着人们继续追问为什么，一层层地追问，永不停止。

两个天才即将相继登场，一个回答了第一个问题，另一个回答了第二个问题。请继续跟着我去一探究竟。