双代号网络计划时间参数的计算

6.3　双代号网络计划时间参数的计算

6.3.1　网络计划的时间参数

如果说网络图的建立是确定一项计划的定性指标，那么，网络计划的计算则是对这项计划的定量描述。网络计划计算的目的在于确定图上各项工作和各个事件的时间参数，找出关键线路和关键工作，为网络计划的执行、控制、调整和优化提供必要的时间依据。计算的内容主要包括：

①ET_i——事件最早时间（Ear1iest event Time）。它表明该事件后各工作的最早可能开始时间；

②LF_i-j——事件最迟时间（1atest event Time）。它表明该事件前各工作的最迟必须完成时间；

③ES_i-j——最早开始时间（Ear1iest Start time）。在紧前工作和有关时限约束下，工作有可能开始的最早时刻；

④EF_i-j——最早完成时间（Ear1iest Finish time）。在紧前工作和有关时限约束下，工作有可能完成的最早时刻；

⑤LF_i-j——最迟完成时间（1atest Finish time）。在不影响任务按期完成和有关时限约束的条件下，工作最迟必须完成的时刻；

⑥LF_i-j——最迟开始时间（1atest Start time）。在不影响任务按期完成和有关时限约束的条件下，工作最迟必须开始的时刻；

⑦TF_i-j——总时差（Tota1 F1oat）。在不影响工期和有关时限的前提下，一项工作可以利用的最大机动时间；

⑧FF_i-j——自由时差（Free F1oat）。在不影响其紧后工作最早开始和有关时限的前提下，一项工作可以利用的机动时间。

时间参数的计算方法有分析计算法、图算法、表算法、矩阵法、电算法等。本教材介绍其中的分析计算法和图算法、表算法。

6.3.2　图算法和分析计算法

图算法是直接在网络图上进行计算的方法，但它是以分析计算法所提出的网络时间参数数学模型为依据的，因此，本节将两者结合起来介绍。

图算法通常直接将网络时间参数标在图上，它适用于工作数目不太多（节点数在20以下）的简单网络计划计算。

图6-22所示网络计划，各工作持续时间标于箭线下方，用图算法和分析计算法计算其时间参数。

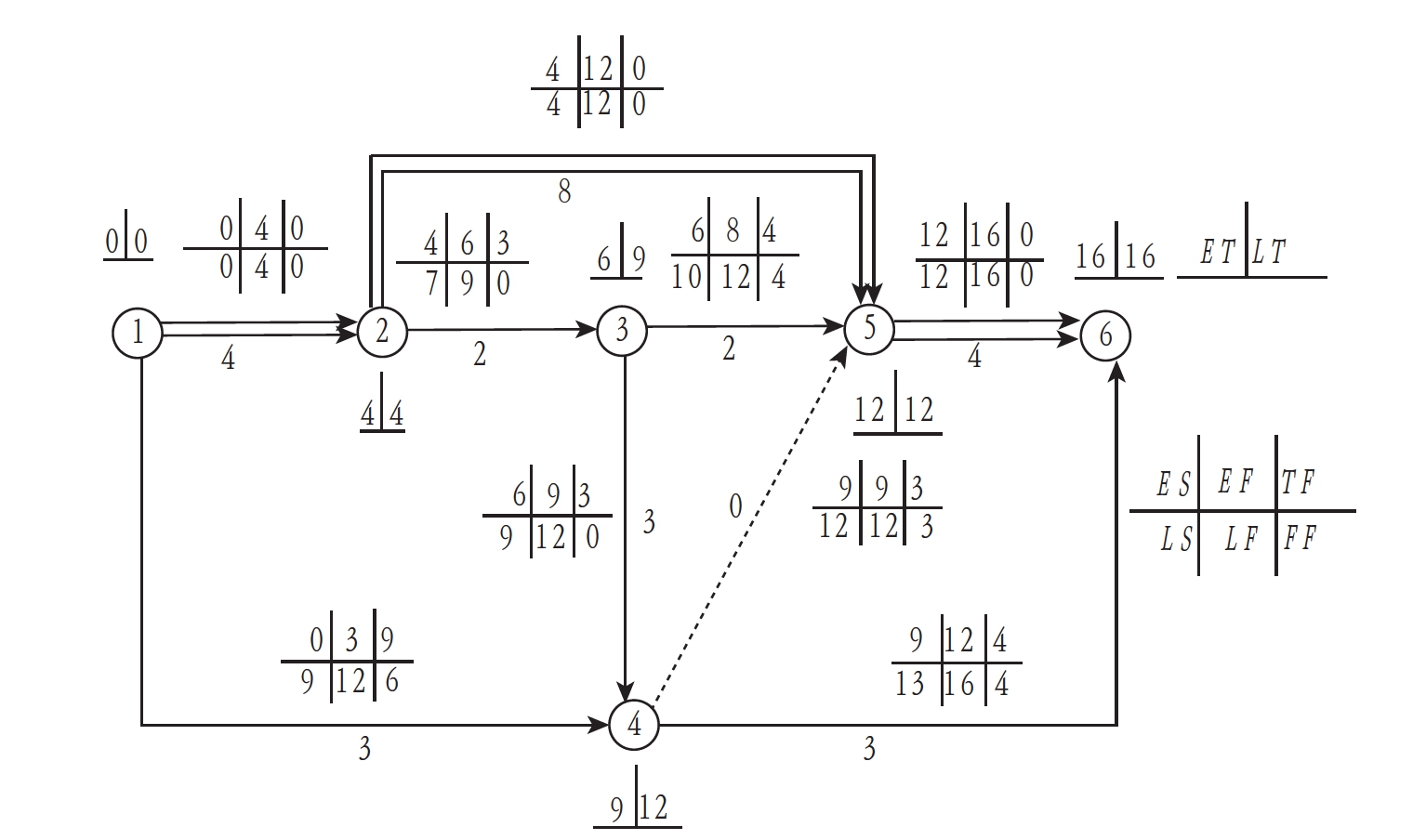
图6-22　双代号网络计划时间参数计算例题

1.计算各事件最早时间ET_j

事件时间参数是以事件为对象计算的，事件最早时间是指该事件后各工作的最早可能开始时间，也就意味着该事件前面各工作的全部最早完成。计算时，根据网络图所确定的顺序关系，按照事件编号从起点事件起依次进行。由于计划从相对时间零天开始，因此，起点事件的最早时间为零，即：

ET_i＝0　　　　（6-3）

式中：ET₁—起点事件1的最早时间。

其他中间事件及终点事件的最早时间，则从事件的紧前事件算起，顺各线路段到达该事件，将紧前事件的最早时间加上各线路段上持续时间之和的最大值，即为该事件的最早时间。由此可得最早时间的计算公式：

ET_j＝max｛ET_i＋ D_i-j｝ （ 1≤i ＜ j ≤ n）　　　　（6-4）

式中：ET_j—事件j的最早时间；

　　　ET_i—事件i的最早时间；

　　　ET_i-j—工作i-j的持续时间。

应用式（6-4）计算事件最早时间，从起点事件开始，定ET₁＝0，然后顺箭线方向逐一算至终点事件，任一事件的最早时间等于该事件的各紧前事件的最早时间，分别加上相应工作持续时间和的最大值。由图6-27计算如下：

ET₁＝0；

ET₂＝ET₁＋D_1-2＝4；

ET₃＝ET₂＋D_2-3＝6；

ET₄＝max｛ET₁＋D_1-4，ET₃＋D_3-4｝＝max｛0＋3＝3，6＋3＝9｝＝9；

ET₅＝max｛ET₂＋D_2-5，ET₃＋D_3-5，ET₄＋D_4-5｝＝max｛4＋8＝12，6＋2＝8，9＋0＝9｝＝12；

ET₆＝max｛ET₄＋ET_4-6，ET₅＋D_5-6｝＝max｛9＋3＝12，12＋4＝16｝＝16。

按（6-4）原理用图算法计算时，先将起点事件最早时间定为0。对网络中的任一事件（除起点事件外的其他事件）的最早时间计算，先在图上找出该事件的所有紧前事件，将这些紧前事件各自的最早时间加上相应的工作持续时间，取其和的最大值即为所求事件的最早时间。依此算至终点事件，即完成全部事件最早时间的计算。对图6-22网络进行计算，其结果标于图中相应位置。用图算法计算事件最早时间可归结为八个字：“沿线累加，逢圈取大。”“沿线累加”是指从网络的起点事件开始，沿着能到达所计算事件的每条线路将各工作的持续时间累加起来；“逢圈取大”是指在每一圆圈（事件）处取到达该圆圈的各条线路累计时间的最大值。

2.计算各事件最迟时间LT_i

事件最迟时间是该事件前各工作的最迟必须完成时间。计算时，从终点事件起，按照事件编号逆向进行。当工期有要求时，终点事件最迟时间等于要求工期；当工期没有规定时，终点事件最迟时间就等于计算工期（即终点事件最早时间），因此：

　　　　（6-5）

式中：LT_n一网络图终点事件最迟时间；

PT—要求工期。

其他事件的最迟时间的算法，则从该事件的紧后事件算起，逆线路段到达该事件，将各紧后事件的最迟时间减去相应线路段上工作的持续时间，取其差的最小值，其计算公式为：

LT_i＝min｛LT_j－D_i-j｝（1≤i＜j≤n）　　　　（6-6）

式中：LT_i—i事件最迟时间；

LT_j—j事件最迟时间。

应用式（6-6）计算时，应按式（6-5）确定出LT_n，然后按事件编号从大到小逐一算至起点事件为止。每次计算时，从网络逻辑关系中搜索其紧后各事件，将紧后各事件的最迟时间分别减去相应工作持续时间之差的最小值，即为所计算事件的最迟时间。对图2-22计算如下:

LT₆＝LT终点＝ET₆＝16；

LT₅＝LT₆－D_5-6＝16－4＝12；

LT₄＝min｛LT₆－D_4-6，LT₅－D_4-5｝＝｛16－3＝13，12－0＝12｝＝12；LT₃＝min｛LT₅－D_3-5，LT₅－D_2-5｝＝min｛12－2＝10，12－3＝9｝＝9；LT₂＝min｛LT₃－D_2-3，LT₅－D_2-5｝＝min｛9－2＝7，12－8＝4｝＝4；LT₁＝min｛LT₂－D_1-2，LT₄－D_1-4｝＝min｛4－4＝0，12－3＝9｝＝0。

按式（6-6）原理用图算法计算时，先根据是否有要求工期定出终点事件的LT_n，然后由终点的紧前事件开始，逆箭线方向逐一算至起点事件为止。每个事件计算时，取其紧后各事件的最迟时间分别减去相应工作持续时间之差的最小值，填入网络图中对应于该事件最迟时间的位置，如图6-22所示。

用图算法计算事件最迟时间也可归结为8个字：“逆线累减，逢圈取小”。“逆线累减”是指从网络的终点事件起逆着每条线路将计划工期依次减去各工作的持续时间；“逢圈取小”是要求在每一圆圈处取其后续线路累减时间的差的最小值。

3.计算最早开始时间ES_i-j和最早完成时间EF_i-j

工作的最早开始时间是在领先于它的紧前工作创造出一定的条件之后，该工作有可能开始的最早时间，而该工作的紧前事件的最早时间正好说明开工条件已经具备，因此：

ES_i-j＝ET_i　　　　（6-7）

式中：ES_i-j—i-j工作的最早开始时间。

若一项工作以其“最早开始时间”开始，经过完成该项工作所需的持续时间以后完成，这个完成的时刻就叫做它的“最早完成时间”，由此可得：

EF_i-j＝ES_i-j＋D_i-j　　　　（6-8）

式中：EF_i-j—i-j工作的最早完成时间。

对图6-22网络图计算如下：

ES_1-2＝ET₁＝0；ES_1-4＝ET₁＝0；

ES_2-3＝ET₂＝4；ES_2-5＝ET₂＝4；

ES_3-4＝ET₃＝6；ES_3-5＝ET₃＝6；

ES_4-5＝ET₄＝9；ES_4-6＝ET₄＝9；

ES_5-6＝ET₅＝12；

EF_1-2＝ES_1-2＋D_1-2＝0＋4＝4；EF_1-4＝ES_1-4＋D_1-4＝0＋3＝3；

EF_2-3＝ES_2-3＋D_2-3＝4＋2＝6；EF_2-5＝ES_2-5＋D_2-5＝4＋8＝12；

EF_3-4＝ES_3-4＋D_3-4＝6＋3＝9；EF_3-5＝ES_3-5＋D_3-5＝6＋2＝8；

EF_4-5＝ES_4-5＋D_4-5＝9＋0＝9；EF_4-6＝ES_4-6＋D_4-6＝9＋3＝12；

EF_5-6＝ES_5-6＋D_5-6＝12＋4＝16。

采用图算法计算时，只要将事件的最早时间照抄即得工作的最早开始时间，然后做一简单加法就得最早完成时间，计算结果如图6-22所示。

4.计算最迟完成时间LF_i-j和最迟开始时间LS_i-j

在项目工期已定的情况下，任何一项工作必定有一个受到这个工期限制的、必须完工的最迟时间。如果该项工作的完工时间不超过这个时间，就不会使后续工作及正程正期受到它的影响而推迟。这个时间就是该项工作的“最迟完成时间”，而按照事件最迟时间的定义，这样一个最迟完成时间应该等于其紧后事件的最迟时间，即：

LF_i-j＝LT_j　　　　（6-9）

式中：LFi-j—i-j工作的最迟完成时间。

对应于一项工作的“最迟完成时间”的开工时间，就是该项工作的“最迟开始时间”，即：

LS_i-j＝ LF_i-j－ D_i-j　　　　（6-10）

对图6-22计算如下：

LF_5-6＝LT₆＝16；LF_4-6＝LT₆＝16；

LF_4-5＝LT₅＝12；LF_3-5＝LT₅＝12；LF_2-5＝LT₅＝12；

LF_3-4＝LT₄＝12；LF_2-3＝LT₃＝9；

LF_1-4＝LT₄＝12；LF_1-2＝LT₂＝4；

LS_5-6＝LF_5-6－D_5-6＝16－4＝12；LS_4-6＝LF_4-6－D_4-6＝16－3＝13；

LS_4-5＝LF_4-5－D_4-5＝12－0＝12；LS_3-5＝LF_3-5－D_3-5＝12＋2＝10；

LS_3-4＝LF_3-4－D_3-4＝12－3＝9；LS_2-5＝LF_2-5－D_2-5＝12－8＝4；

LS_2-3＝LF_2-3－D_2-3＝9－2＝7；LS_1-4＝LF_1-4－D_1-4＝12－3＝9；

LS_1-2＝LF_1-2－D_1-2＝4－4＝0。

采用图算法时，只要将节点的抄于工作i-j的LF_i-j处，然后作一简单减法即可得LS_i-j，如图6-22所示。

5.计算总时差TF_i-j

工作的总时差是在不影响工期的前提下，一项工作可以利用的机动时间。从图6-22已计算出的时间参数中可以看出，在计算工期不变的条件下，有些工作的ES_i-j（或EF_i-j）与LS_i-j（或LF_i-j）之间存在一定差值，只要工作i-j的开始时间在此范围内变动，则对总工期没有影响；而工作开始时间的变动超过此范围，则肯定会影响工期。因此，这个差值就是工作的总时差TF_i-j，即：

TF_i-j＝ LS_i-j－ ES_i-j＝ LF_i-j－ EF_i-j　　　　（6-11）

式中：TF_i-j—i-j工作的总时差。

从式（6-11）可看出，一项工作的总时差实际上也是在不影响其紧后工作按最迟开始时间开工的前提下，该工作可以利用的机动时间。

图6-27各工作的TF_i-j计算如下：

TF_1-2＝LS_1-2－ES_1-2＝0－0＝0；TF_1-4＝LS_1-4－ES_1-4＝9－0＝9；

TF_2-3＝LS_2-3－ES_2-3＝7－4＝3；TF_2-5＝LS_2-5－ES_2-5＝4－4＝0；

TF_3-4＝LS_3-4－ES_3-4＝9－6＝3；TF_3-5＝LS_3-5－ES_3-5＝10－6＝4；

TF_4-5＝LS_4-5－ES_4-5＝12－9＝3；TF_4-6＝LS_4-6－ES_4-6＝13－9＝4；

TF_5-6＝LS_5-6－ES_5-6＝12－12＝0。

图算法结果如图6-22所示。

6.计算自由时差FF_i-j

自由时差FF_i-j是指一项工作完成后，在不影响其紧后工作按最早开始时间开始的前提下，该项工作可以利用的机动时间的最大值。而一项工作只要能保证其完成事件按最早时间ET_i发生，就肯定能保证其紧后工作按最早开始时间开始。从而有：

FF_i-j＝ ET_j－EF_i-j　　　　（6-12）

式中：FF_i-j—i-j工作的自由时差。

图6-22各工作的FF_i-j计算如下：

EF_1-2＝ET₂－EF_1-2＝4－4＝0；FF_1-4＝ET₄－EF_1-4＝9－3＝6；

EF_2-3＝ET₃－EF_2-3＝6－6＝0；FF_2-5＝ET₅－EF_2-5＝12－12＝0；

FF_3-4＝ET₄－EF_3-4＝9－9＝0；FF_4-6＝ET₆－EF_4-6＝16－12＝4；

FF_5-6＝ET₆－EF_5-6＝16－16＝0。

图算法结果标于图6-22中。

7.确定关键工作和关键线路

（1）关键工作。

网络计划中总时差最小的工作为关键工作。如果没有工期规定，则关键工作的TF_i-j为0。图6-22中，工作①→②、②→⑤、⑤→⑥的总时差TF＝0。它们都是关键工作，其余工作则为非关键工作。

（2）关键线路。

网络计划中，自起点事件至终点事件全由关键工作组成的线路为关键线路。实际上，它也是网络计划中线路上工作总持续时间最长的线路。一个网络计划中，可能存在一条或多条关键路线，关键线路是网络计划实施中的控制重点。图6-22中，自起点事件①将TF_i-j＝0的工作依次连接起来直至终点事件⑥所形成的线路①—②—⑤—⑥（图中用双线表示）即为一条关键线路。

网络计划中，除关键线路外的其他线路都是非关键线路。非关键线路的重要程度也各有不同。有些非关键线路其线路上工作总持续时间与关键线路非常接近（线路时差很少），这样的非关键线路称为次关键线路。“网络计划实施过程中，由于环境或计划自身的变化，次关键线路最有可能转变为关键线路，所以在计划实施中也应严密注视次关键线路。

8.总时差TF_i-j与自由时差FF_i-j的关系

从图6-23中可以看出，某些工作的总时差与其自由时差是相互关联的。也就是说，动用本工作的自由时差不会影响紧后工作的最早开始时间，而在本工作总时差范围内动用机动时间（时差）若超过本工作自由时差范围，则会相应减少后续工作拥有的时差，并会引起该工作所在线路上所有后续非关键工作，以及与该线路有关的其他非关键工作时差的重新分配。如上例中（图6-22）①→④→⑥线路，其中EF_1-4＝6，FF_4-6＝4。若工作①→④动用机动时间为4（小于6），则对后续各工作的最早开始时间和时差均无影响；若工作①→④动用机动时间为8（大于6，超过FF_1-4），则会引起④→⑥的自由时差减少2，即④→⑥的自由时差调整为FF_4-6＝4－2＝2，总时差也相应调整为TF_4-6＝4－2＝2。由于事件④的时间参数有所变化，因而也引起紧后虚工作④—⑤的时差调整：FF_4-5＝3－2＝1，TF_4-5＝3－2＝1。此例明确地表明了TF_i-j与FF_i-j间的关系。

工作的总时差和自由时差具有如下性质：

①总时差不为某个工作所专有而与前后工作有关，它为一条线路（或线段）所共有；自由时差虽也不为某个工作所专有，但利用自由时差对后续工作没有影响；

②FF_i-j≤TF_i-j。对无工期要求的网络计划，若TF_i-j＝0，则FF_i-j＝0；

③对无工期要求的网络计划.以关键线路上的事件为紧后事件的工作，则有：TF_i-j＝FF_i-j；

④对无工期要求的网络计划，TF_i-j＝0的工作即为关键工作，由于关键线路上各工作的时差均为零，则关键线路的长度必然决定计算工期。

在实际工作中，应用时差具有重要意义。时差的应用主要有两个方面：

①组织均衡施工。由于非关键工作具有时差，在时差范围内改变非关键工作的开始和完成时间，从而调整逐日的资源需用量，以达到均衡施工的目的。

②合理赶工。由于决定工期的是关键工作，它不能耽搁，而非关键工作在时差范围内延误不影响工期。由此可利用时差充分调动非关键工作的人力、物力资源来确保关键工作的加快或按期完成，从而使总工期目标得以实现。

图6-23　自由时差与总时差的关系