数据的整理和分析

12.3　数据的整理和分析

如前所述，工程质量会发生波动。由于质量的波动，自然会引起质量检测数据的参差不齐，有时还会发现一些明显过大或过小的异常数据，我们称这些数据为特异数据或可疑数据。特异数据出现的原因有多种，可能是试验条件的变化，也可能是检测对象质量分布不均匀，或者由于测试操作者缺少经验等。如果有特异数据混入整个质量检测数据之中，将可能导致对检测结果分析判断出完全不同的结论（错误结论）。因此，在进行数据分析以前，有必要对这些特异数据作甄别处理或将其从整个数据中剔除。

甄别处理特异数据的准则有3σ准则、肖维勒准则、格拉布斯准则、狄克松准则等。

12.3.1　3σ准则

如果质量检测数据的总体服从正态分布X～N（μ，σ²），由3σ^[1]原则知，对于每个质量数据落在区间（μ－3σ，μ＋3σ）内的概率为99.73％，而落在这个区间外面的概率仅为0.27％，即1 000次测量中只可能出现3次。因此，在有限的测量中发生这种情况的可能性是很小的，而一旦有这样的数据出现，则可认为它是可疑数据，应予以剔除。

当总体的标准差σ未知时，以样本标准差S估计σ，并以3S代替3σ。3σ准则比较适用于样本容量n＞50的情况。

判断方法如下：

设X₁，X₂…X_K，X_n是从总体中抽取的样本，其中X_K为过大或过小值。

①计算数据的平均值X^„，如总体标准偏差σ未知时，同时求出样本标准偏差S；

②计算｜X_K－X^„｜，如果：

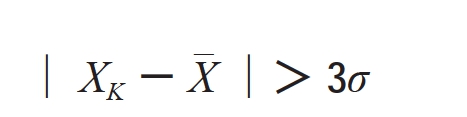　　　　（12-7）

则将X_K剔除，否则保留。

12.3.2　肖维勒准则

设X₁，X₂…，X_n是从总体抽取的样本。

肖维勒准则判断特异数据的方法如下：

①计算样本平均值X„，如总体标准偏差σ未知时，同时求出样本标准偏差S；

②对样本中最大或最小的值X_i，计算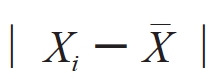，如果：

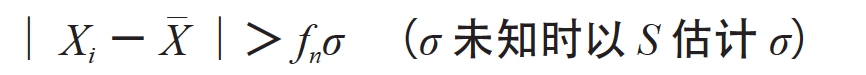　　　　（12-8）

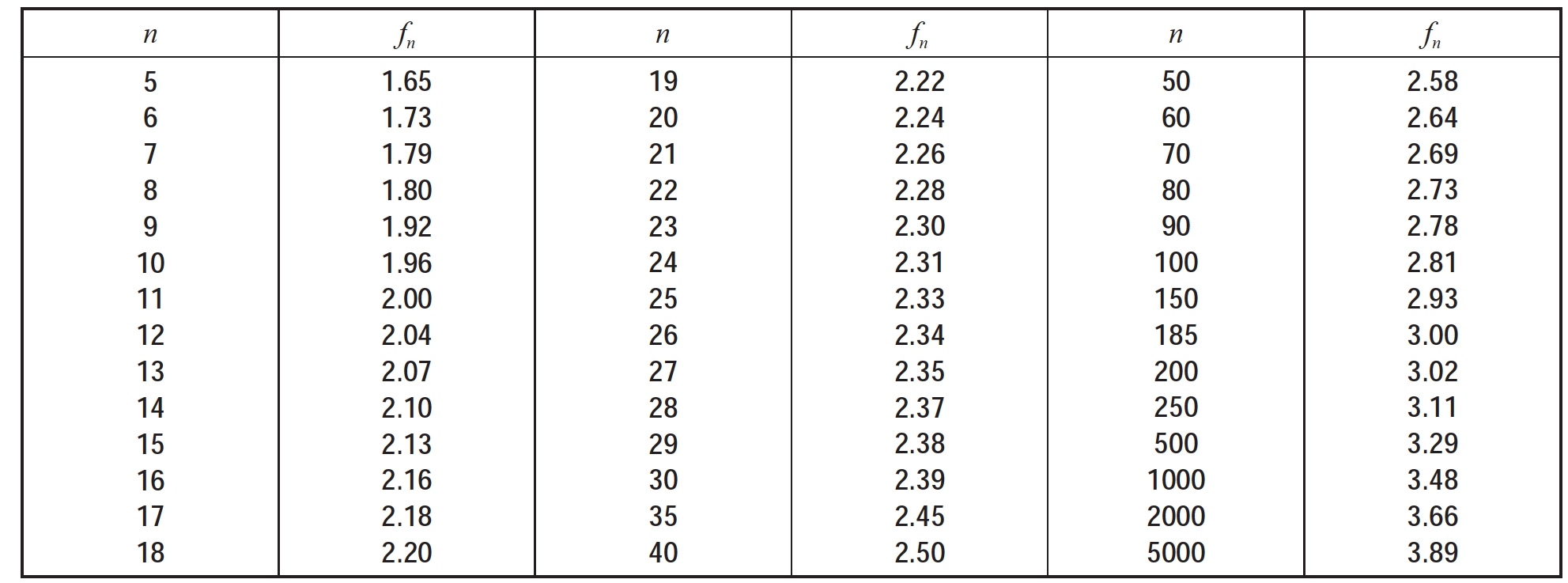
则将X_i剔除，否则保留。上式中f_n是与样本容量n有关的系数，可查表12-2。

表12-2　肖维勒准则f_n数值表

12.3.3　格拉布斯准则

设X₁，X₂…，X_n是从总体中抽取的样本。

格拉布斯准则判断特异数据的方法如下：

（1）计算样本平均值X„，如总体标准偏差σ未知时，同时求出样本标准偏差S；

（2）对样本中最大或最小的值X_i，计算｜X_i－X^„｜，如果

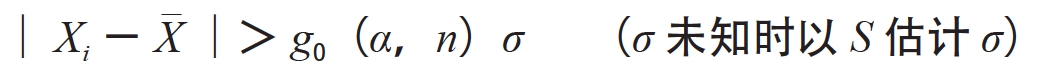　　　　（12-9）

则将X_i剔除，否则保留。

上式中g₀（α，n）是一个与样本容量n及给定的检验水平α（即把不是可疑的数据错判为可疑数据而被剔除的概率）有关的系数。α通常取0.05和0.01，g₀（α，n）的值列于表12-3中。

表12-3　格拉布斯准则g₀（α，n）数值表

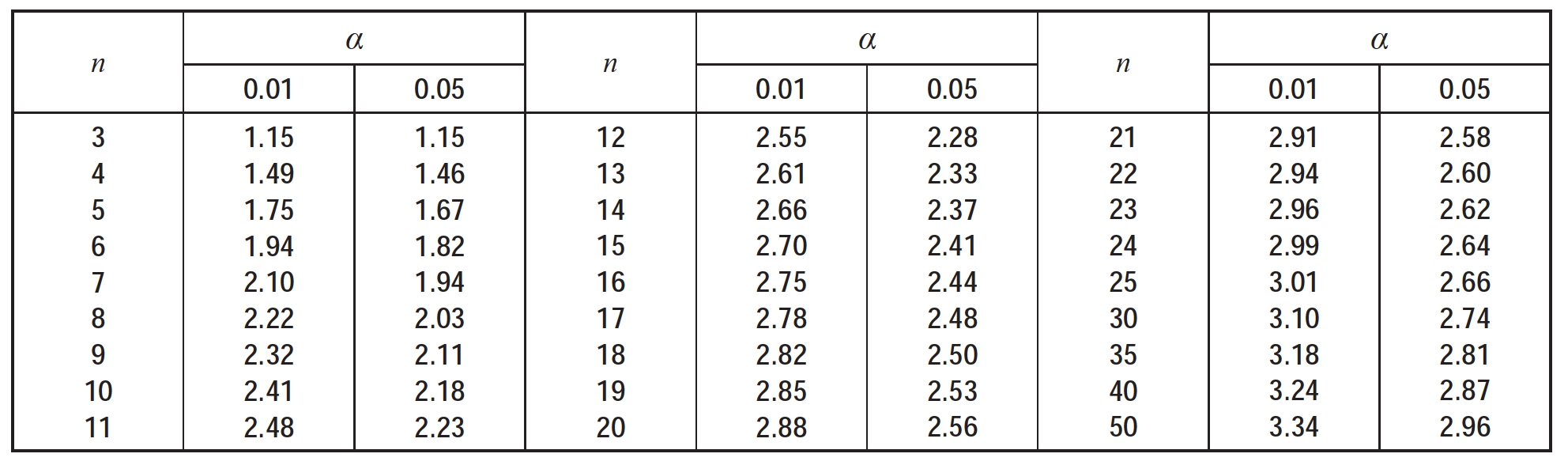
格拉布斯准则比较适用于样本容量n≤25的情况。

12.3.4　狄克松准则

前面三种在总体标准差σ未知时，均需求出样本标准偏差S，实际应用中比较麻烦，而狄克松准则用极差比的方法，可得到简捷而严密的结果。

判断方法如下：

设X₁，X₂…，X_n是从总体中抽取的样本。

（1）将n个样本观测值按值太小，依次从小到大排列如下：

其中，X_（1）（i＝1，2，…，n）表示按值大小将样本观测值重新排列后，处于第i位置的样本值。

（2）对于不同的样本容量n，从表12-4中查出相应的统计量γ_ij（例如n＝12），并且判断样本的最大值X（n）是否为可疑数据时，采用统计量：

表12-4　狄克松准则统计量γij表

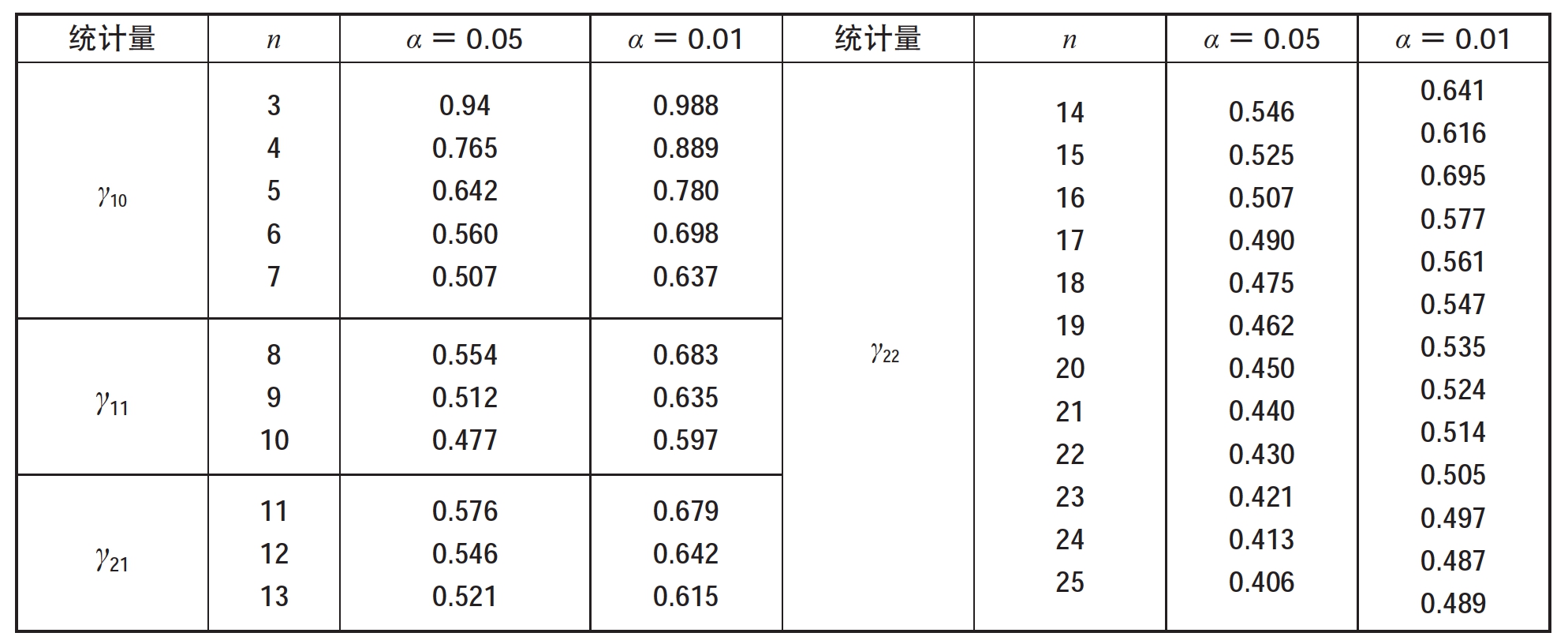
（3）由给定的检验水平α，从表12-5中查出临界值γ_ij，α，如n＝12，α＝0.05时，由表12-5查出临界值γ₂₁，_0.05＝0.546。

表12-5　狄克松准则临界γ_ij,α表

（4）由样本观测值计算γ_ij，如果：

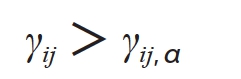　　　　（12-10）

则判断X_（n）［或X_（1）］是可疑数据，应予剔除，否则保留。如n＝12，α＝0.05时，由样本观测值计算γ₂₁，当γ₂₁＞γ_21，0.05＝0.546时，将X_（n）剔除，否则保留。

12.3.5　应用上述四种判断准则时的注意点

①剔除可疑数据时，首先应对样本观测值中的最小值和最大值进行判断，因为这两个值极有可能是可疑数据。

②可疑数据每次只能剔除一个，然后按剩下的样本观测值重新计算，再做第二次判断，如此逐个地剔除，直到所有剩下的值不再是可疑数据为止。不允许一次同时剔除多个样本观测值。

③采用不同准则对可疑数据进行判断时，可能会出现不同的结论，此时要对所选用准则的适用范围、给定的检验水平的合理性，，以及产生可疑数据的原因等作进一步的分析。

【例】对一盘混凝土，取15个试件进行抗压强度试验，测试结果如下：（单位：Mpa）

31.2，33.1，30.5，31.0，32.3，31.2，29.4，24.0

30.4，33.0，32.2，31.0，28.6，29.2，30.3

试判断这些数据中是否混有可疑数据。

【解】分别用不同准则进行判断，以此进行比较：

（1）3σ准则：

n＝15，X_max＝33.1，X_min＝24.0，„

首先，怀疑最小值24.0。对数据进行统计计算，得X＝30.49，S＝2.23，3S＝6.69。

｜24.0－30.49｜＝6.49＜6.69＝3S

说明此值在3S内，不应剔除。

其次，怀疑最大值33.1。同上计算，得：

｜33.1－30.49｜＝2.61＜6.69＝3S

故33.1应保留。全部数据中均无可疑数据，无须剔除。

（2）肖维勒准则：

由n＝15，查表12-2得f_n＝2.13，并计算出：

X^„＝30.49，S＝2.23 f_nS＝2.13×2.23＝4.75

首先，怀疑最小值24.0，由于

｜24.0－30.49｜＝6.49＜4.75＝f_nS，

故认为特异数据24.0应剔除。

对剩下的14个样本观测值重新计算得X„'＝30.96，S'＝1.37，由n＝14在表12-2中查出f_n＝2.01，并算出f_nS＝2.10×1.37＝2.88。再对其中的最大值33.1和最小值28.6怀疑。因

｜33.1－30.96｜＝2.14＜2.88

及　　　　　　　　｜28.6－30.96｜＝2.36＜2.88，

所以认为33.1和28.6均应保留。

至此，全部数据中已不再含有可疑数据。

采用格拉布斯准则和狄克松准则也可得出应剔除24.0特异数据而保留其他数据的结论。由此例计算结果表明，3σ准则相对于其他准则在特异数据取舍方面偏于保守。