扭力扳手的使用

活动一　扭力扳手的使用

在拧紧轮胎或缸盖等重要部分的螺栓时，并不是越紧越好，而是规定有一定数值的力矩（俗称“扭力”）。我们可以使用扭力扳手来达到这种要求。

1.汽车修理工常用的呆扳手，其手柄部分的长短是根据所拧螺栓的直径规格而定的。

2.什么时候需要用扭力扳手？使用时应注意什么问题？

一、选择合适的扳手拧紧螺母

操作尝试：用正常扳手拧紧螺母，感觉手上用力；在正常扳手手柄上加上套筒拧紧相同类型螺母，再感觉手上用力，发现拧紧相同类型的螺母，后者用力比前者轻。可见手柄部分越长，其力臂就越长，在同样的力作用下，则力矩也越大。若呆扳手手柄长度不受到限制，就有可能把小直径的螺栓拧断。

二、用扭力扳手来拧紧发动机气缸盖或主轴承的螺栓与螺母

发动机气缸盖或主轴承的螺栓与螺母拧紧要求很高，通常要用扭力扳手控制力矩大小，拧紧时要严格按照规定的顺序和力矩大小要求，通过看扭力扳手上的扭转力矩刻度来控制。如图5－1－1和图5－1－2所示：

图5－1－1　扭紧缸盖螺栓（操作手势演示）

图5－1－2　通过指针观察施加的扭力

一、力矩与力矩的平衡条件

1.力矩

力是物体运动状态改变的原因，力不仅能使物体移动，还能使物体转动，我们用力矩来解释物体的转动效应。

以扳手拧螺母为例。如图5－1－3所示，设螺母能绕O点转动，作用在扳手的力F在与螺母轴线垂直的平面内，力F的作用线到O点的垂直距离为d。转动中心O点称为力矩中心，简称矩心。O点至力F的作用线的垂直距离d称为力臂。

力F使物体绕O点转动的效应，取决于下列两个因素：①力的大小与力臂的乘积Fd；②力使物体绕O点转动的方向。通常规定：力使物体绕矩心逆时针方向转动的力矩为正，反之为负。以上两个因素可用一个代数量±Fd来概括，用公式记为

图5－1－3　力矩

M_O（F）＝±Fd

力矩的单位在国际单位制中常用N·m（牛·米）。

力矩在下列两种情况下等于零：①力等于零；②力的作用线通过矩心，即力臂为零。

由经验可知：螺母拧紧的程度不仅与力F的大小有关，而且与点到力的作用线的垂直距离d有关。同样大小的力，如果d越长，螺母就拧得越紧。反过来，如果d很短，要拧紧螺母就要花费很大的力气。

另外，如果我们改变力的方向，则力的作用效果也随之改变。若在扳手上加一个反向力，则可拧松螺母。显然，力F使扳手绕O点转动的方向不同，则其效应也就不同。

2.合力矩定理

平面汇交力系的合力对平面内任意点为矩，等于所有各分力对同一点之矩的代数和。这个关系称为合力矩定理，它的数学表达式为

M_O（R）＝M_O（F₁）＋M_O（F₂）＋…＋M_O（F_n）＝∑_O（F）

例5－1　如图5－1－4所示，圆柱直齿传动中，已知轮齿啮合面间的作用力F_n＝1kN，啮合角α＝20°，齿轮分度圆直径d＝60mm。试计算力对轴心O的力矩。

解　方法一：根据力矩的定义来求

MO（F_n）＝F_n·h＝F_n·（D/2）·cosα＝28.2（N·m）

方法二：根据合力矩定理来求

将力F_n沿半径r方向分解成一组正交的圆周力F_t＝F_ncosα与径向力F_r＝F_nsinα。

图5－1－4　例5－1图

MO（F_n）＝M_O（F_t）＋MO（F_r）＝F_t·r＋0＝F_ncosα·r＝28.2（N·m）

3.力矩的平衡

如图5－1－5所示，力FA促使杆AB绕O点作逆时钟方向转动，而力FB促使杆AB绕O点作顺时针方向转动，当FA和FB分别对O点产生力矩的大小相等、方向相反时，转动效应互相抵消，杆AB处于平衡状态。

图5－1－5　力矩的平衡

由此可知，所有绕定点转动物体平衡的共同规律。如果在绕定点转动的物体上作用有n个力，各力对转动中心O点的力矩分别为MO（F₁），MO（F₂），…，MO（F_n），则绕定点转动物体的平衡条件是：各力对转动中心O点的矩的代数和等于零，即合力矩等于零。用公式表示为

MO（F₁）＋MO（F₂）＋…＋MO＝0

记为

∑MO（F）＝0

上式称为力矩平衡方程。

利用力矩平衡方程，可以分析和计算杠杆、绞车、滑轮等绕定点（或定轴）转动的简单机械在平衡时，某些未知力的大小。

二、力偶与力偶矩

1.力偶

在日常的生活和生产实际中，我们时常会看到汽车司机用双手转动转向盘驾驶汽车；人们用两个手指头旋转钥匙开门；用两个手指头拧开或关紧水龙头。如图5－1－6所示，转向盘、钥匙、水龙头为何会转动？这是因为人们对这些物体施加了等值、反向的一对平行力。这种由两个大小相等、方向相反的一对平行力组成的力系，叫做力偶。

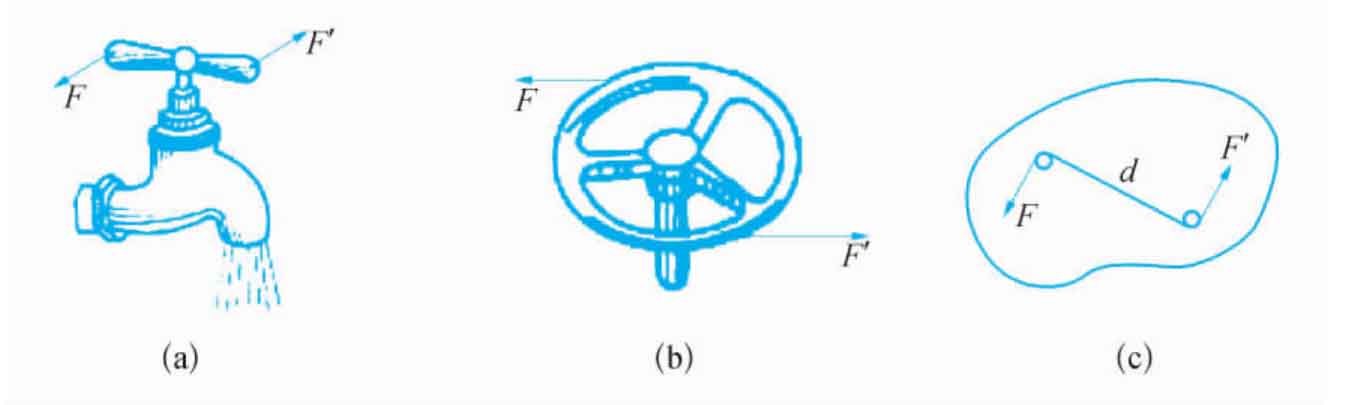
图5－1－6　力偶

①力偶是大小相等、方向相反且不共线的两个力所组成的力系。所以力偶就是一个最简单、最基本的力系，记作（F，F′）。

②力偶对物体的作用效果是改变物体的转动状态。

力使物体绕某点转动的效应可用力矩来度量，同理力偶使物体转动的效应可由力偶的两力对点的合力矩来度量。

在图5－1－6中，由力F与F′对转动中心的合力矩为

力偶中两个力之间的距离d，称为力偶臂。力偶中的力F与力偶臂d的乘积，称为力偶矩。力偶对物体转动效应的大小由力偶矩来度量。

力偶（F，F′）的力偶矩，以符号M（F，F′）表示，或简写为M，那么就有

M＝±Fd

如图5－1－7所示，设物体上作用一力偶臂为d的力偶（F，F′），力偶对任一点O的矩为

M＝MO（F）＋MO1（F′）＝F（d＋a）－F′a＝Fd

图5－1－7　力偶矩

从上式可看出，力偶对物体的转动作用决定于力偶中力的大小和两个力之间的距离，而与矩心位置无关。即：

力偶矩的大小等于力与力偶臂的乘积，其正负号表示力偶的转向。力偶矩的正负规定与力矩相同，即：逆时针方向转动为正，顺时针方向转动为负。

力偶矩的单位与力矩的单位相同。

力偶中两个力所在的平面，称为力偶作用面，受力偶作用的物体在此平面内转动。

力偶对物体的转动效应，取决于下列三要素：

①力偶矩的大小；

②力偶矩的转向；

③力偶的作用平面。

2.力偶的性质

性质1　力偶既无合力，也不能和一个力平衡，力偶只能用力偶来平衡。

性质2　力偶对其作用面内任一点之矩恒为常数，且等于力偶矩，与矩心的位置无关。

性质3　力偶可在其作用面内任意转移，而不改变它对刚体的作用效果。

性质4　只要保持力偶矩的大小和转向不变，可以同时改变力偶中力的大小和力偶臂的长短，而不改变其对刚体的作用效果。