车桥受力分析

活动二　汽车悬架、车桥受力分析

汽车悬架是汽车里重要的一个组成部分，其作用有以下两点：①尽量保持车轮与地面的接触；②减少震动，提高乘坐的舒适度。悬架的组成包括弹性组件、减振器和传力装置等3部分，这3个部分分别起缓冲、减振和力的传递作用。

请观察非独立悬架结构图，如图5－2－1所示。图5－2－2为汽车后桥的简化受力分析。

图5－2－1　非独立悬架结构图

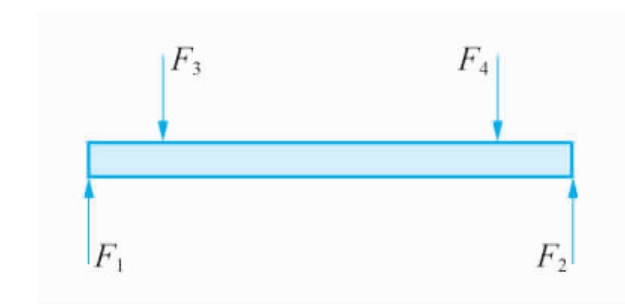
图5－2－2　后桥简化受力分析图

汽车的悬架系统及受力分析如图5－2－3所示。

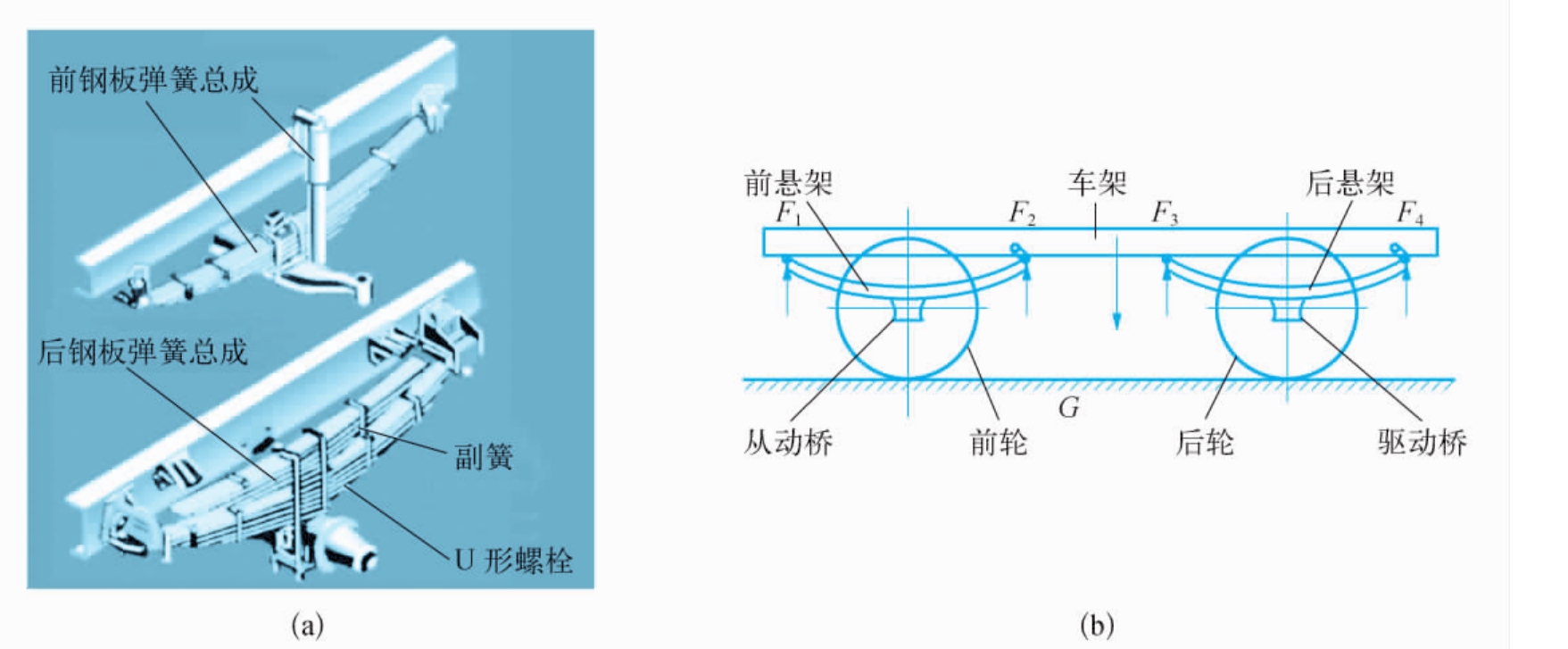
图5－2－3　悬架系统及受力分析

1.观察后桥及悬架的结构和组成。

2.初步分析后桥主要部件的受力情况。

一、平面平行力系

力系中各力的作用线都在同一个平面内，并且相互平行，这样的力系为平面平行力系。如图5－2－4所示。

1.平面平行力系的平衡条件与平衡方程

如图5－2－4所示，设物体受到平面平行力系F₁、F₂、F₃、F₄的作用。如选取x轴与各力垂直，那么各力在x轴上的投影必定为零，自然满足∑^Fx＝0。所以平面平行力系独立的平衡方程式数目只有两个，即：

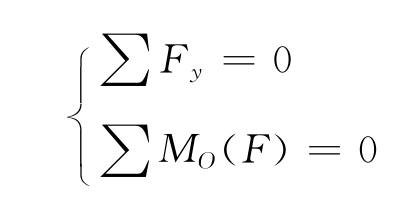
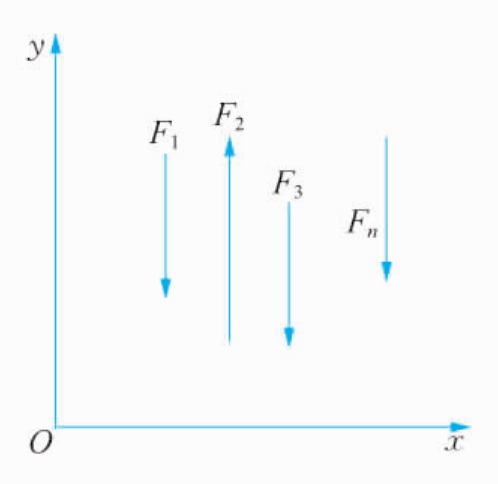
图5－2－4　平面平行力系

因此平面平行力系的平衡条件为：力系中所有各力的代数和等于零；所有各力对平面内任意一点的合力矩等于零。

平面平行力系的平衡方程常常采用另外一种形式，即：

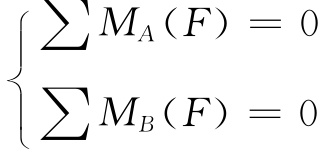
也就是说，力系中所有各力对平面内任意两点的合力矩均等于零。应当指出的是，A、B两点的连线，不能与力系中的各力平行。

2.平面平行力系平衡方程的应用

下面以一实例来说明平面平行力系平衡方程的应用。

例5－2　汽车起重机的车重G＝20kN，起重机旋转及固定部分重W1＝30kN，起重臂重W2＝4kN，尺寸如图5－2－5所示，设起重臂在起重机对称平面内，并且放在最低位置，求车辆不至于翻倒的最大起重量W3，以及车轮受到地面的约束反力。

解　取整台汽车起重机为研究对象。其上面的作用力G、W₁、W₂、W₃、R_A、R_B组成了一平面平行力系，由平衡条件∑^MB＝0，可得：R_A×3.8－G×2＋W₂×2.5＋W₃×5.5＝0

当W3增加到汽车不至于翻倒的临界值时，为安全起见，必须RA≥0。所以

RA＝（2G－2.5　W₂－5.5　W₃）÷3.8≥0得W_3max＝5.45（kN）

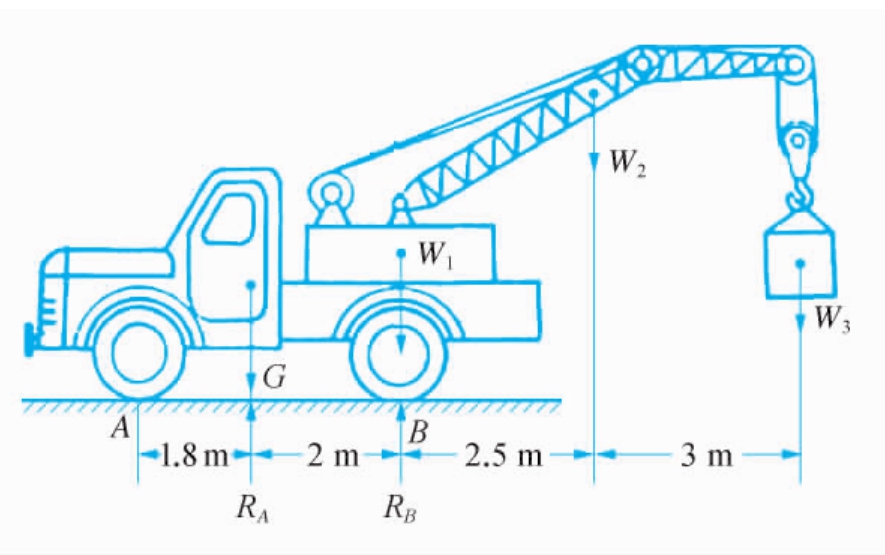
图5－2－5　汽车起重机

对于后轮支座反力，有∑F_y＝0，则

R_A＋R_B＝G＋W₁＋W₂＋W₃

因为　R_A＝0

所以　R_B＝59.45（kN）

二、平面任意力系

作用于物体上的各力，其作用线任意地分布在同一平面内，它们既不汇交于一点，又不全部相互平行，这样的力系称为平面任意力系。

1.平面任意力系的平衡条件与平衡方程

起重机的水平梁AB受到平面任意力系的作用，力系中的各力不但能使水平梁AB产生沿x轴方向和y轴方向移动的趋势，而且还能使水平梁AB产生在力系所在的平面内转动的趋势。若要使水平梁AB在各力作用下仍然保持平衡，首先，水平梁AB在各力作用下不能沿x轴方向或y轴方向产生移动，因此必须满足：

∑F_x＝0，　　∑F_y＝0

另外，水平梁AB也不能绕力系所在平面内任意一点产生转动，即：

∑M_O（F）＝0

由此可以得到平面任意力系的平衡条件：力系中所有各力，在两个互相垂直的坐标轴上投影的代数和等于零，力系中所有各力对力系所在平面内任意点的合力矩等于零。即：

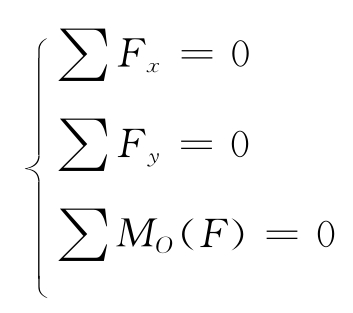
上式称为平面任意力系的平衡方程，由两个投影式和一个力矩式组成，它是平面任意力系的平衡方程，共有3个独立的方程，可以求解不超过3个未知量的平衡问题。

2.平面任意力系平衡方程的应用

应用平面任意力系平衡方程求解实际问题时，首先要建立工程结构和构件的平面力学模型；其次确定研究对象，取其分离体，画受力图；然后列平衡方程求解。

（续　表）

一、填空题

1.力矩的力臂就是　　到矩心的垂直距离，力矩的大小等于力的大小和力臂的　　，力矩在国际单位制中用　　作单位。

2.力偶是一对　　、　　的　　力。

3.力偶的三要素是力偶的　　、　　和　　。

4.力偶矩相同的力偶是　　，它们可以互相　　。

5.平面汇交力系和平面平行力系是　　的两种特殊形式。

6.受平面任意力系作用的物体处于平衡的条件：一是物体所受的　　等于零；二是物体所受的　　等于零。

二、是非题

1.力对刚体某点的力矩大小，将因为沿其作用线移动而变化。（　　）

2.力偶不仅能使物体移动，而且能使物体转动。　　　　　　（　　）

3.力偶可以在其作用面内任意转移，而不改变它对刚体的作用，因为转移并不改变其力偶矩。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

4.力偶的两力大小相等、方向相反，因此它们的合力为零。　（　　）

5.任何力系都可用一合力来代替。　　　　　　　　　　　　（　　）

三、简答题

1.何谓合力矩定理？

2.平面力偶系平衡的条件是什么？