正弦电路发生谐振啥意思

时间：2022-11-06 百科知识版权反馈

【摘要】：正弦交流电路是指含有正弦交流电源而且电路中各部分所产生的电压和电流均按正弦规律变化的电路，简称交流电路。正弦交流电具有容易产生、传输经济、便于使用等特点，目前在工农业生产和生活中得到广泛应用。本模块首先学习正弦交流电的基本概念、基本理论，然后训练正弦交流电路的基本分析方法，为学习后续内容打基础。因此，正弦交流电常用相量表示，以便将三角运算简化成复数形式的代数运算。

子模块二　正弦交流电路

一、正弦交流电的基本概念

正弦交流电路是指含有正弦交流电源而且电路中各部分所产生的电压和电流均按正弦规律变化的电路，简称交流电路。正弦交流电具有容易产生、传输经济、便于使用等特点，目前在工农业生产和生活中得到广泛应用。

资料卡

正弦交流电的产生

正弦交流电（Alternating Current，AC）是正弦交流发电机产生的，图1.48是正弦交流发电机原理图。正弦交流发电机的主要部分是线圈和磁极线圈：多用铜线绕成矩形，有许多匝，匝数越多，产生的感应电动势越大。磁极：至少一对，多的达40对以上。磁极对数越多的发电机，产生的交流电的变化速度越快。图1.48中发电机的磁极对数为一对。

图1.48　正弦交流发电机原理图

1. 磁极中线面的磁感应强度最强，为B_m；电枢表面上其他位置的磁感应强度按正弦函数规律变化：若线圈平面与磁极中性面的夹角为α，则线圈导体所处的磁感应强度为B=B_msinα。

2. 磁感应强度方向与导体的运动方向垂直，即v⊥B。设线圈的有效长度为l，线圈平面以角速度ω逆时针方向旋转，与磁极中性面夹角为α，假定从a指向d的电动电动势为正，从d指向a的电动电动势为负，则线圈产生的感应电动势的大小为：e = Blvsin(v，B)= B_msina·l·vsin 90°= B_mlvsina=E_msina，式中，E_mE_mlv=，表示交流电动势的最大值。

可见，这个电动势是按正弦函数规律变化的，我们把它称为正弦交流电动势。

本模块首先学习正弦交流电的基本概念、基本理论，然后训练正弦交流电路的基本分析方法，为学习后续内容打基础。

大小和方向随时间作周期性变化且在一个周期内的平均值为零的电压、电流和电动势统称为交流电。日常所用的交流电源（含信号源）其电压、电流和电动势一般都是随时间按正弦规律变化的，故称之为正弦交流电源或正弦交流信号，统称正弦量。正弦量可用三角函数式表示，例如正弦交流电流可表示为

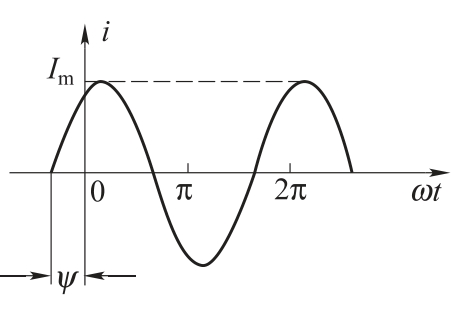
图1.49　正弦交流电波形图

其波形如图1.49所示。其中i表示瞬时值或瞬时值表达式。mI为最大值（幅值）、ω为角频率、ψ为初相位。

幅值、角频率、初相位分别表征正弦变化的大小、快慢和初始值。它们是确定一个正弦量的三个要素。

下面分别对它们进行学习和训练。

（一）周期、频率、角频率

正弦量变化一周所需的时间称为周期，用T表示，单位为秒（s）。每秒钟变化的次数称为频率，用f表示，单位为赫兹（Hz）。周期和频率互为倒数，即

我国和世界上很多国家电网工业频率（简称工频）为50Hz，美国、日本等国家的工频为60Hz。高频加热炉频率为200～300kHz。无线电通信频率为30kHz～3×10⁴MHz。

正弦量变化的快慢还可用角频率ω来表示，因为正弦量一周期内经历弧度为2π，所以其角频率为

它的单位为弧度每秒（rad/s）。

练一练

已知u(t)100sin(100πt-30°)=V，则频率f是多少？

（二）最大值与有效值

正弦量在任一瞬间的值称为瞬时值，用小写字母表示，如i、u、e分别表示电流、电压和电动势的瞬时值。瞬时值中最大的值称为最大值（或幅值），用带下标m的大写字母表示，如I_m、U_m和E_m分别表示电流、电压和电动势的最大值。

通常计量交流电大小的既不是瞬时值，也不是最大值，而是交流电的有效值。它是这样定义的：如果某一个周期交流电流i通过电阻R在一个周期T内产生的热量和另一个直流电流I通过同样大小的电阻在相等的时间内产生的热量相等，则把这一直流电流I的值定义为该交流电流i的有效值。据此可得：

故交流电的有效值为：

即交流电的有效值等于瞬时值的平方在一个周期内的平均值再开方。故有效值又称为方均根值。

对于正弦交流电流msin()iItωψ=+，代入（1.2.4）式则有：

同理，对于正弦电压和电动势，有

由式（1.2.5）、（1.2.6）、（1.2.7）可见，正弦量的最大值是有效值的2倍，式中大写字母I、U和E分别表示电流、电压和电动势的有效值。

资料卡

交流电压和电流大小

通常所说的交流电压和电流的大小，例如交流电压220V和380V，以及一般交流测量仪表所指示的电压、电流的数值都是指的有效值。

想一想　　某电容器额定耐压值为450V，能否把它接在交流380V的电源上使用？为什么？

（三）初相位

正弦量在不同时刻t由于具有不同的tωψ+值，正弦量也就变化到不同的数值，所以tωψ+反映出正弦量变化的进程，称为正弦量的相位角，简称相位。

t=0时的相位称为初相位。显然，初相位与所选时间的起点有关。原则上，计时的起点是可以任选的。但同一个电路中所有的电流、电压和电动势只能有一个共同的计时起点。初相位决定了t=0时正弦量的大小和正负。一般选择||πψ≤。

在同一线性正弦交流电路中，电压、电流与电源的频率是相同的，但初相位不一定相同。

两个同频率的正弦量的相位之差称为相位差，用ϕ表示，如图1.50所示。

　　u=U_msin(ωt+ψ₁)

　　i=I_msin(ωt+ψ₂)

它们的相位差：

　　ϕ=(ωt+ψ₁)−(ωt+ψ₂)=(ψ₁−ψ₂)

可见，同频率正弦量的相位差也就是初相位之差。

当两个同频率的正弦量的计时起点（t=0）改变时，它们的相位和初相位也随之改变，但两者之间的相位差保持不变。

由图1.50可见，由于ψ₁>ψ₂，ϕ=ψ₁-ψ₂>0，所以，u较i先到达正的最大值（或零值），这时称在相位上u比i超前ϕ 角，或称i比u滞后ϕ 角；若ϕ <0，则正好相反。若ϕ =0，即ψ₁=ψ₂，则称u和i相位相同，或称u与i同相，如图1.51（a）所示。

若ϕ=±π，则称u与i相位相反，或称u与i反相，如图1.51（b）所示。

图1.50　u和i的相位差

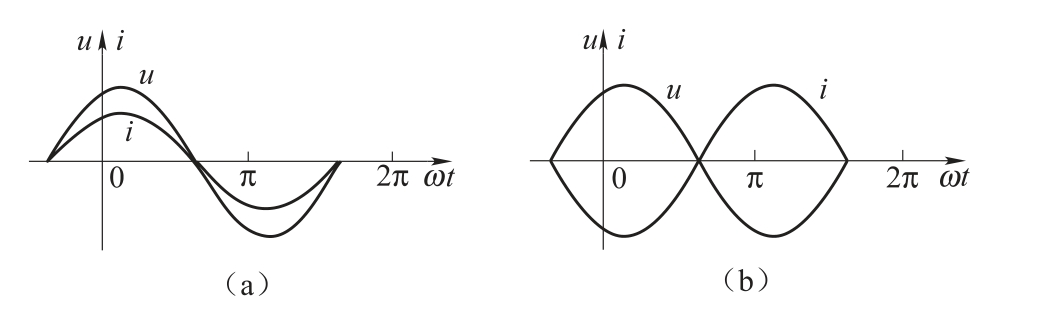
图1.51　同频率正弦量的同相与反相

（a）同相；（b）反相

练一练

已知一正弦信号源的电压幅值为10mV，初相位为30°，频率为1 000Hz，求电压瞬时值表达式？

二、正弦量的相量表示法

如上节所述，正弦量有幅值、频率及初相位三个要素，可用三角函数式和波形图表示一个正弦量。在交流电路的分析和计算中，常需将频率相同的正弦量进行加减等运算，若采用三角运算和波形图法都不够方便。因此，正弦交流电常用相量表示，以便将三角运算简化成复数形式的代数运算。

图1.52　复平面的旋转矢量

（a）旋转矢量；（b）波形

在图1.52（a）所示的复平面中，有一个长度为r、与实轴正方向夹角（初始角）为ψ、角速度为ω、逆时针方向旋转的矢量A，任一瞬间在虚轴上的投影为sin()rtωψ+，波形如图1.52（b）所示。正好与正弦交流电的波形图相同。因而，如果用一个旋转矢量来表示正弦量，就是用矢量的长度、旋转角速度和初始角分别代表正弦量的最大值、角频率和初相位，那么同频率正弦量之间的三角运算可以简化为复平面中的矢量运算。

由于同频率的正弦量用旋转矢量表示时，它们旋转角速度相等，任一瞬间它们的相对位置不变。为简化运算，可以将它们固定在初始位置，用复平面中处于起始位置的固定矢量来表示一个正弦量，如图1.53所示，由于正弦交流电不是矢量，故称该表示正弦量的固定矢量为相量，并用大写字母上面加“· ”的方式表示。如果相量长度等于最大值则称为最大值相量，符号为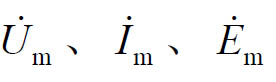，如图1.54所示。该图又称相量图。

图1.53　矢量与复数

图1.54　相量图

由于正弦量的大小通常是用有效值表示的，且。故正弦量也可用复平面中长度等于正弦量的有效值、初始角等于正弦量的初相位的固定矢量来表示，并称之为有效值相量，用表示。

想一想　　正弦量的表示方法有几种？如何表示？

复平面中的任一矢量都可以用复数来表示，因而相量也可以用复数来表示。复平面上的矢量A，长度为r，与实轴正方向的夹角为ψ，在实轴上的投影为a，在虚轴上的投影为b，可表示为

　　A=a+jb　　　　　　　　　　　　　（代数式）

　　=r∠ψ　　　　　　　　　　　　（极坐标式）

　　=re^jψ　　　　　　　　　　　　　　（指数式）

　　=rcosψ+jrsinψ　　　　　　　　（三角函数式）

它们之间关系为

利用这些关系可在四种表达式中进行转换。一般来说，复数的加减运算用代数式，其实部与实部相加减，虚部与虚部相加减；乘除运算常用极坐标式，两复数的模相乘除，辐角相加减。

其中，j=，是虚数的单位，其极坐标式为：

　j=1∠90°

同理，−j=1∠−90°

在复数运算中，当一个复数乘上j时，其模不变，辐角增大90°，而当一个复数除以j时，其模不变，辐角减少90°。相量的复数表达式即为正弦量的相量表示式。

据此，两个同频率的正弦量：

用最大值相量表示为

有效值相量表示为

其相量图如图1.55所示

必须指出，正弦量可以用相量表示，但相量不等于正弦量。例如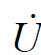_m=U∠ψ_u≠U_msin(ωt+ψ_u)，读者应注意区分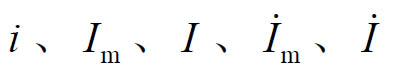（或）五种符号的不同含义。

在线性正弦交流电路中，由于电压、电流全部是同频率的正弦量，故可以导出基尔霍夫定律的相量式，也就是∑i=0和∑u=0的相量形式可表示为：

利用基尔霍夫定律的相量式就可将三角运算简化为复数形式的代数运算。

［例1.2.1］已知i₁=。求i=i₁+i₂。

解：由

所以　

也可先画出相量图，如1.56所示。

图1.55　i与u的相量图

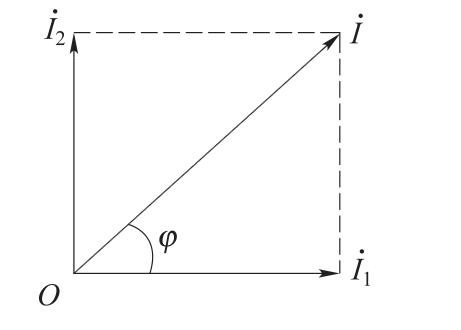
图1.56　例1.2.1所用的图

想一想　　例1.2.1中I和I₁+I₂是否相等？如果不相等，为什么？

根据平行四边形法则，由图1.56可得

练一练

1. 已知380sin(45)ut=−°（V），用相量法表示，并画出相量图。

2. 向量可以表示正弦量，是不是就可以认为它们相等?如果不相等请说明原因。

三、单一参数的正弦交流电路

电阻、电感和电容是组成电路的基本元件，本节分别讨论正弦交流电路中电阻、电感和电容的电压与电流的关系及其相量模型和功率。

（一）纯电阻电路

1. 电压与电流关系

图1.57（a）所示电阻电路中，为了方便起见，以为参考相量：

　　i=I_msinωt

根据欧姆定律

　　u=Ri=RI_msinωt=U_msinωt　　　　　　　　　　　（1.2.12）

可见u与i不但是同频率的正弦量，而且u、i同相，其波形如图1.57（b）所示。

由式（1.2.12）可知，电阻的电压与电流之间的关系为：

（1）大小关系　U_m=RI_m

　　　　　　　 U=RI

（1.2.13）

（2）相位关系ψ_u=ψ_i

（3）相量关系=I∠0°

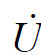　　　　　　 =U∠0°= RI∠0°

即　

或　

其相量图如图1.58（a）所示，图1.58（b）称为电阻的相量模型。

图1.57　电阻电路及其u、i、p波形

（a）电路；（b）u、i及p波形

图1.58　电阻的电压、电流相量图和相量模型

（a）相量图；（b）相量模型

2. 功率

（1）瞬时功率

由P=UI得

其波形曲线如图1.57（b）所示。可见p总为正值，电阻总是吸收能量，将电能转换为热能，所以电阻是耗能元件。

（2）平均功率

电路在一个周期内消耗电能的平均值，即瞬时功率在一个周期内的平均值，称为平均功率，又称有功功率，用大写字母P表示，即

电阻元件的平均功率

（二）纯电感电路

1. 电压与电流关系

图1.59（a）所示的电感电路中，设

则：

可见其u与i是同频率的正弦量，且u比i超前90°，其波形如图1.59（b）所示。

图1.59　电感电路及其u、i、p波形

（a）电路；（b）u、i及p波形

由式（1.2.18）可得电感电压与电流之间的关系如下。

（1）大小关系

上式中，X_L为电压有效值与电流有效值之比，称为感抗。由

可知，电感对交流电流有阻碍作用，频率越高，则感抗越大，其阻碍作用越强。在直流电路中f=0，X_L=0，电感可视为短路。

感抗X_L的倒数又称为感纳B_L，即

（2）相位关系

（3）相量关系

由　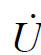=I∠°0

得　

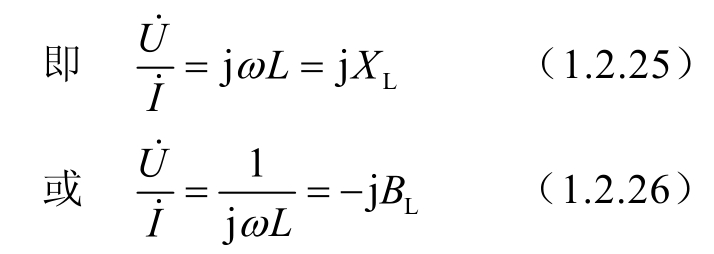
图1.60　电感的电压、电流相量图和相量模型

（a）相量图；（b）相量模型

电感的电压、电流的相量图如图1.60（a）所示，图1.60（b）为电感的相量模型。

2. 功率

（1）瞬时功率

由式（1.2.15）：

其波形曲线如图1.59（b）所示。当|i|增大时，p>0，电感从电源吸收能量，磁场能量增加，电能转变为磁场能量；当|i|减小时，p<0，电感释放能量，磁场能量减小，磁场能量转变为电能，归还电源。

（2）平均功率

可见电感元件不消耗能量，只与电源交换能量，是储能元件。

（3）无功功率

为了衡量电感元件与电源交换能量的规模大小，将瞬时功率的最大值定义为无功功率Q。即

为了与有功功率区别，其单位用乏（var）或千乏（kvar）。

资料卡

无功功率

无功功率决不是无用功率，它的用处很大。电动机需要建立和维持旋转磁场，使转子转动，从而带动机械运动，电动机的转子磁场就是靠从电源取得无功功率建立的。变压器也同样需要无功功率，只有无功功率才能使变压器的一次线圈产生磁场，在二次线圈感应出电压。因此，没有无功功率，电动机就不会转动，变压器也不能变压，交流接触器不会吸合。

在正常情况下，用电设备不但要从电源取得有功功率，同时还需要从电源取得无功功率。如果电网中的无功功率供不应求，用电设备就没有足够的无功功率来建立正常的电磁场，那么这些用电设备就不能维持在额定情况下工作，用电设备的端电压就要下降，从而影响用电设备的正常运行。

［例1.2.2］图1.59（a）电路中，已知u=200sin(ωt+60°)V，L=0.318H。求：（1）f= 50Hz时，电流i和无功功率Q；（2）f=500Hz时，电流i又是多少？

解：（1）f=50Hz时

（2）f=500Hz时

练一练

1. 使用电感时，若电感两端的正弦交流电压频率上升5%，电压有效值上升5%，则电感中的电流会发生什么变化？

2. 如图1.61所示，瓦特计的读数为2kW，U=230V，f=50Hz，现将一纯电感L=0.1H并接到电路中，则瓦特计的读数为。

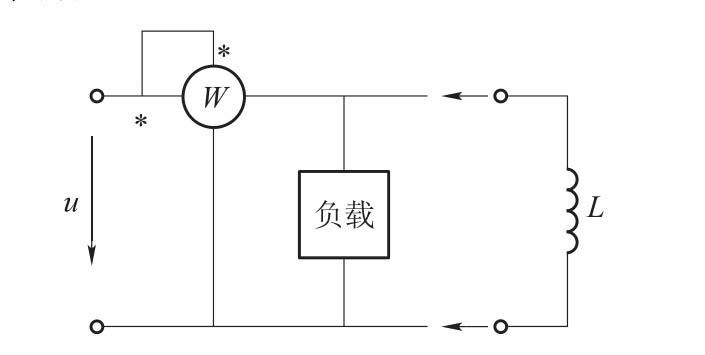
图1.61　练习图12

（三）纯电容电路

1. 电压与电流关系

图1.62（a）所示的电容电路中，设

　　u=U_msinωt

则：

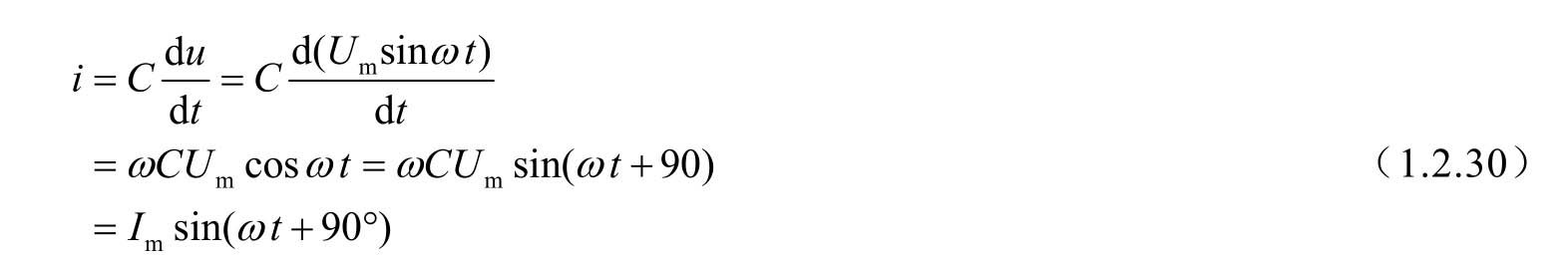
图1.62　电容电路及其u、i及p波形

（a）电路；（b）u、i及p波形

可见其u与i是同频率的正弦量，且i比u超前90°，波形如图1.62（b）所示。

由式（1.2.30）可得电容电压与电流之间关系：

（1）大小关系

上式中，CX为电压与电流有效值之比，称为容抗。由

可知：电容对交流电流有阻碍作用，频率越低，则容抗越大，其阻碍作用越强。在直流电路中0f=，CX=∞，电容可视为开路。

容抗CX的倒数CB称为容纳，即

（2）相位关系

　　 ψ_i=ψ_u+90°

（3）相量关系

电容的电压与电流相量图如图1.63（a）所示，图1.63（b）为电容的相量模型。

2. 功率

（1）瞬时功率

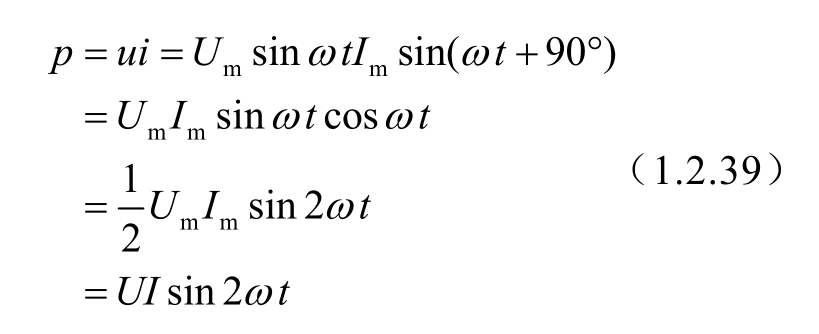
图1.63　电容的电压、电流相量图和相量模型

其波形曲线如图1.62（b）所示，当|u|增大（a）相量图；（b）相量模型时，p>0，电容从电源吸收能量，电场能量增加，电能转变为电场能量；当|u|减小时，p<0，电容释放能量，电场能量减小，电场能量转变为电能归还电源。

（2）平均功率

可见电容元件不消耗能量，只与电源交换能量，是储能元件。

（3）无功功率

为了同电感元件电路的无功功率相比较，也设设i=I_msinωt 。

则　u=U_msin(ωt-90°)

于是p=ui=-UIsin2ωt

由此可得电容的无功功率

即电容的无功功率取负值，以示区别。

［例1.2.3］图1.62（a）所示电路中，以知u=200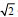sin(314t+30°)V，C=31.8μF求：电流i、无功功率Q和电容的最大储能W_cm

解：B=ωC=314×31.8×10⁻⁶=1×10⁻²（S）

练一练

1. 使用电容器时，电容两端的交流电压有效值上升10%，其他不变，则电容器上的电流发生什么变化？

2. 如图1.64所示，瓦特计的读数为2kW，U=230V，f =50Hz，现将一纯电容C=96μF并接到电路中，则瓦特计的读数为_______。

图1.64　练习图13

四、R、L、C串联的正弦交流电路

电阻、电感和电容元件串联的交流电路如图1.65（a）所示，图1.65（b）是它的相量模型。设i=I_msinωt，即以为参考相量。

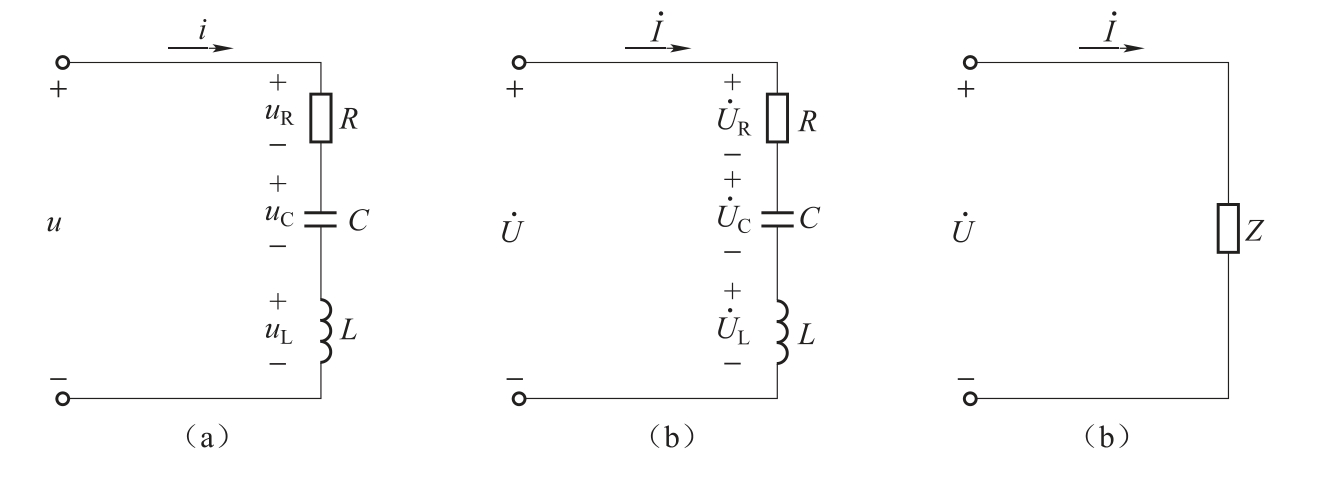
图1.65　R、L、C串联电路

（a）电路；（b）相量模型；（c）等效电路

（一）电压与电流关系

根据KVL有

　　u=u_R+u_L+u_C

用相量表示，则

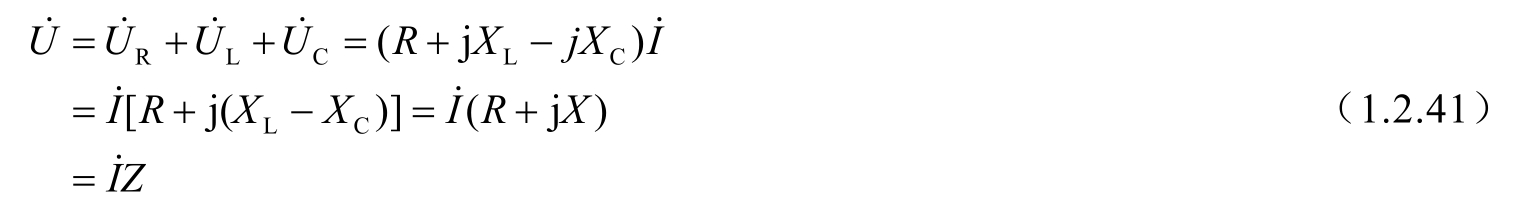
式中，X=X_L−X_C称为电抗，Z则称为电路的等效阻抗。

　　　Z=|Z|∠ϕ=R+jX=R+j(X_L−X_C) （1.2.42）

可知

阻抗模

由式（1.2.43）和（1.2.44）可知，R、X和||Z组成一直角三角形，称为阻抗三角形，如图1.66所示。

电压与电流的相量关系式：

图1.66　阻抗三角形

也称为相量形式的欧姆定律。

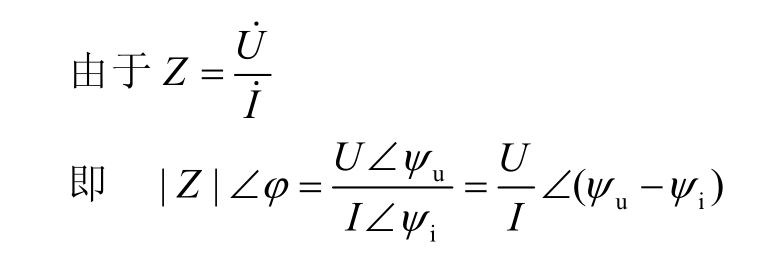
可得电压和电流之间的关系为：

① 大小关系

② 相位关系ϕ=ψ_u−ψ_i

（1.2.46）

由式（1.2.46）可知阻抗角ϕ就是电压与电流间的相位差，其大小由电路参数决定。根据（1.2.44）式，当

X>0（即X_L>X_C）时，ϕ>0，u超前i，电路呈电感性。

X<0（即X_L<X_C）时，ϕ<0，u滞后i，电路呈电容性。

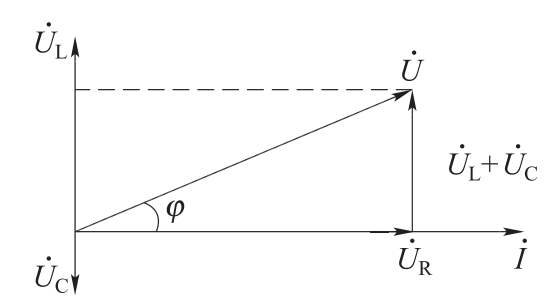
图1.67　R、L、C串联电路的相量图

X=0（即X_L=X_C）时，ϕ=0，u与i同相，电路呈电阻性。

以电流为参考相量，根据纯电阻、电感和电容的电压与电流的相量关系及总电压相量等于各部分电压相量之和，可画出电路中的电流和各部分电压的相量图，如图1.67所示，图中各电压组成一个直角三角形，利用相量图也可得到电压与电流的关系。

（二）电路的功率

1. 瞬时功率

2. 有功功率

上式表明：交流电路中，有功功率的大小，不仅取决于电压和电流的有效值，而且和电压、电流间的相位差ϕ（阻抗角）有关，即与电路的参数有关。式中，cosϕ称为电路的功率因数。

由相量图中的电压三角形可知

上式说明交流电路中只有电阻元件消耗功率，电路中电阻元件消耗的功率就等于电路的有功功率。

3. 无功功率

电路中电感和电容元件要与电源交换能量，相应的无功功率为

　　Q=U_LI−U_CI=I(U_L−U_C)=UIsinϕ 　　　　　　　　　　　　　（1.2.51）

4. 视在功率

交流电路中，电压有效值U与电流有效值I的乘积称为电路的视在功率，用S表示。即

　　S=UI　　　　　　　　　　　　　　　（1.2.52）

视在功率的单位为伏安（V·A）或千伏安（kV·A）。

根据前面的分析，由于

　　P=UIcosϕ

　　Q=UIsinϕ

　　S=UI

可知有功功率P、无功功率Q和视在功率S之间也组成一个直角三角形，称为功率三角形，如图1.68所示，三者之间关系为：

图1.68　功率三角形

功率三角形与电压三角形和阻抗三角都是相似三角形。交流发电机和变压器等供电设备都是按照一定的输出额定电压U_N和额定电流I_N设计制造，两者的乘积称为设备的，额定视在功率S_N，即

　　S_N=U_NI_N（1.2.56）

使用时，若实际视在功率超过额定视在功率，设备可能损坏，故其额定视在功率又称额定容量，简称容量。

［例1.2.4］如图1.65（a）所示的R、L、C串联电路中，已知u=220sin(314t+30°)V，R=30Ω，L=127mH，C=40μF。求：（1）感抗X_L、容抗X_C；（2）电路中的电流i及各元件电压U_R、U_L和U_C；（3）电路的有功功率P、无功功率Q和视在功率S。

解：该电路的相量模型如图1.65（b）所示。

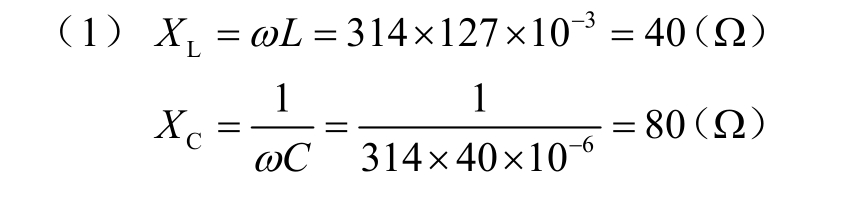
（2）电路的等效复阻抗

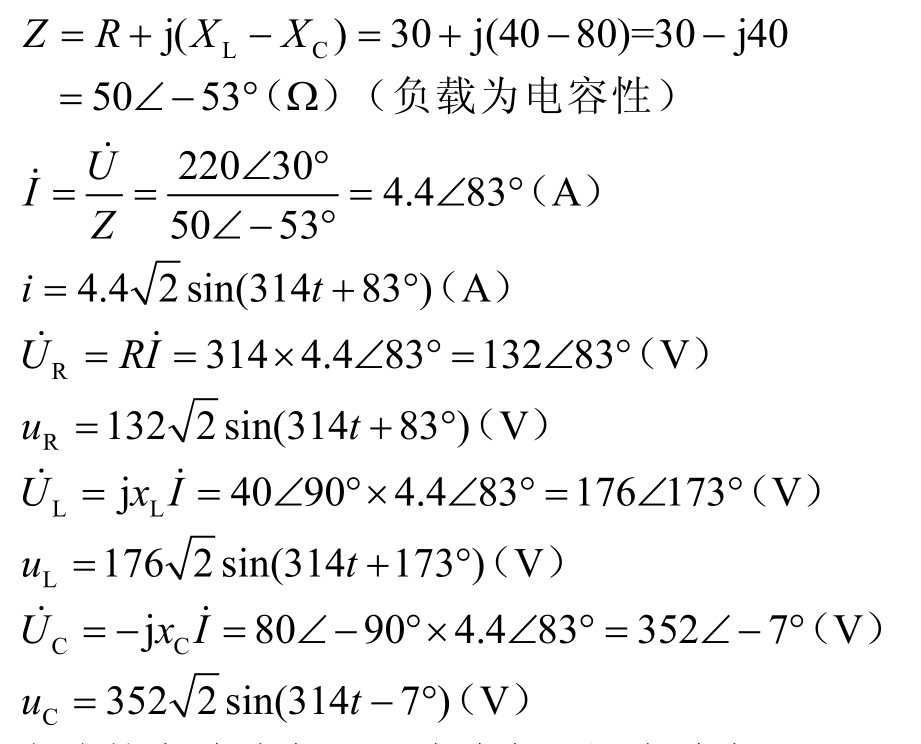
（3）电路的有功功率、无功功率和视在功率

　　 P=UIcosϕ=220×4.4×cos(−53°)=581（W）

　　 Q=UIsinϕ=220×4.4×sin(−53°)=−774（var）

　　 S=UI=220×4.4=968（ViA）

资料卡

电容性负载

电容性负载又叫容性负载。和电源相比，负载电流超前负载电压一个相位差，此时负载为容性负载（如补偿电容负载）。电路中类似电容的负载，可以使电流超前电压降低电路功率因数。

R、L、C串联电路包含了三种性质不同的参数，是具有一定意义的典型电路。若电路中只有其中两种参数串联，分析时，可视为R、L、C串联电路在R、X_L、X_C中某个等于零的特例。

练一练

1. 在图1.69所示的串联正弦交流电路中，R=10Ω，X_L=20Ω，X_C=30Ω，则：（1）电路中各电压有何向量关系？（2）电源电压u与i谁超前？

图1.69　练习图14

2. R、L串联电路接于220V直流电源时，测得其电流为22A；当接于220V、50Hz交流电源时，测得电流为11A，则可确定感抗X_L是多少？

五、R、L、C并联的正弦交流电路

电阻、电感和电容元件并联的交流电路如图1.70（a）所示，图1.70（b）是它的相量模型，设msinuUtω=，即以为参考相量。

图1.70　R、L、C并联电路

（a）电路；（b）相量模型；（c）等效电路

（一）电压与电流关系

根据KCL

　　i=i_L+i_C+i_L

用相量表示，则

式中，B=B_C−B_L，称为电纳；Y则称为电路的等效导纳，等效电路如图1.70（c）所示。

由 Y=|Y|∠θ=G+jB=G+j(B_C−B_L)可知：　　　　　　　　（1.2.58）

图1.71　导纳三角形

导纳模

导纳角

G、B和|Y|可组成一直角三角形，称为导纳三角形，如图1.71所示。由电压与电流间的相量关系式

可得电压和电流之间的关系为

① 大小关系：

② 相位关系：θ=ψ_i−ψ_u　　　　　　　　　　（1.2.62）

由式（1.2.62）知导纳角θ，也就是电流与电压间的相位差，其大小由电路参数决定。根据式（1.2.60），当

B>0（即B_C>B_L）时，θ>0，i导前u，电路呈电容性；

B<0（即B_C<B_L）时，θ<0，i滞后u，电路呈电感性；

B=0（即B_C=B_L）时，θ=0，i与u同相，电路呈电阻性。

又因

（即R、L、C并联电路既可等效为一导纳Y，也可等效为一阻抗Z，导纳和阻抗是互为倒数的关系。）

即有

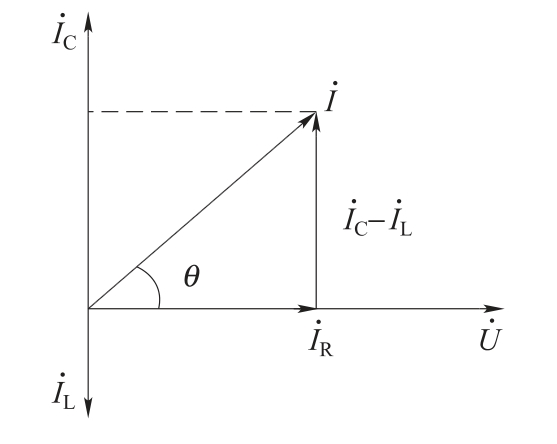
图1.72　R、L、C并联电路相量图

　　θ=−ϕ

以电压为参考相量，根据纯电阻、电容和电感的电流与电压的相量关系，及总电流相量等于各支路电流相量之和，可画出电路中电压和各电流的相量图，如图1.72所示。各电流组成一电流三角形。

利用相量图也可得电压与电流关系：

（二）功率

用与R、L、C串联电路同样的方法可推得功率。

1. 瞬时功率

　　p=ui=UI[cosθ−cos(2ωt+θ)]

2. 有功功率

3. 无功功率

当电容的无功功率定义为负值时

4. 视在功率

P、Q和S组成的功率三角形，与导纳三角形及电流三角形亦为相似三角形。

R、L、C三个参数并联电路也是一定意义上的典型电路，对于只有其中两个参数并联的电路，分析时，可视为R、L、C并联电路在G、B_C、B_L中某个等于零的特例。

R、L、C并联电路与R、L、C串联电路，又是互为对偶的电路。在熟悉了R、L、C串联电路之后，利用对偶原理，就很容易掌握R、L、C并联电路。

资料卡

对偶原理

运筹学中的一个原理。例如R和G互为对偶，电压u和i互为对偶，串联和并联互为对偶。

练一练

如图1.73所示，三个灯泡D₁、D₂、D₃在f=50Hz时亮度相同，当f=60Hz时，三个灯泡亮度关系？（设D为亮度）

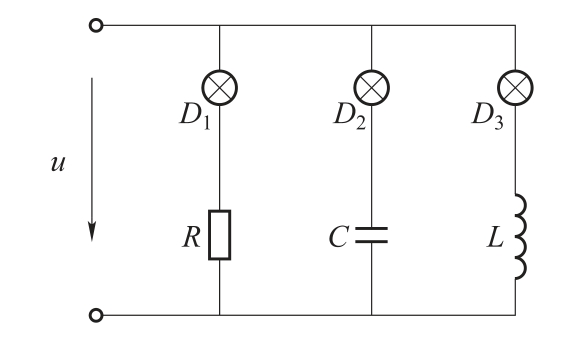
图1.73　练习图15

六、阻抗的串联和并联

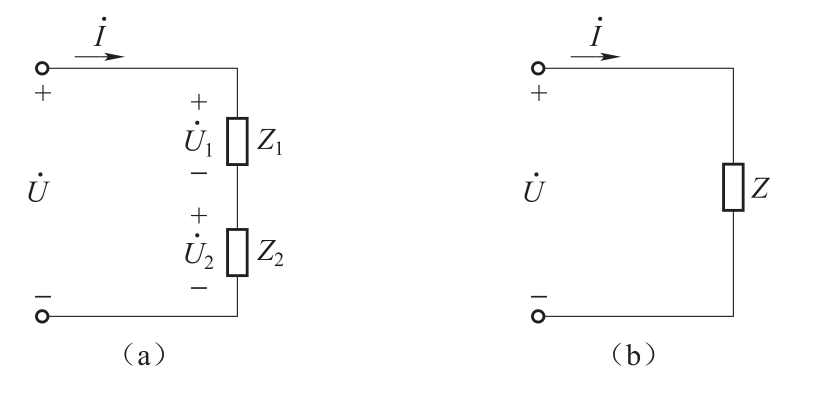
图1.74　阻抗串联及其等效电路

（a）阻抗串联；（b）等效电路

（一）阻抗的串联

阻抗的串联电路如图1.74（a）所示。

阻抗的串联电路具有下列特点：

① 各阻抗流过同一电流。

② 总电压满足以下关系：

式中，Z为电路的等效阻抗，等效电路如图1.74（b）所示。

③ 等效阻抗满足以下关系：

　　Z=Z₁+Z₂　　　　　　　　　（1.2.69）

即等效阻抗等于各串联阻抗之和。一般当几个阻抗串联时：

　　Z=∑Z_K=∑R_K+j∑X_K=|Z|∠ϕ　　　　　　　　　　　　　（1.2.70）

式中，∑X_K中感抗X_L取正号，容抗X_C取负号。

④ 每个阻抗两端的电压满足以下关系：

注意：一般U≠U₁+U₂，|Z|≠|Z₁|+|Z₂|。

练一练

1. 在电感、电容、电阻串联的交流电路中，若电阻为6Ω，感抗为12Ω，容抗为4Ω，则电路的阻抗是多少？

2. 在图1.74（a）中，为什么12UUU≠+？请简要说明原因。（二）阻抗的并联阻抗的并联电路如图1.75（a）所示。阻抗的并联电路，采用导纳并联分析比较方便，设：

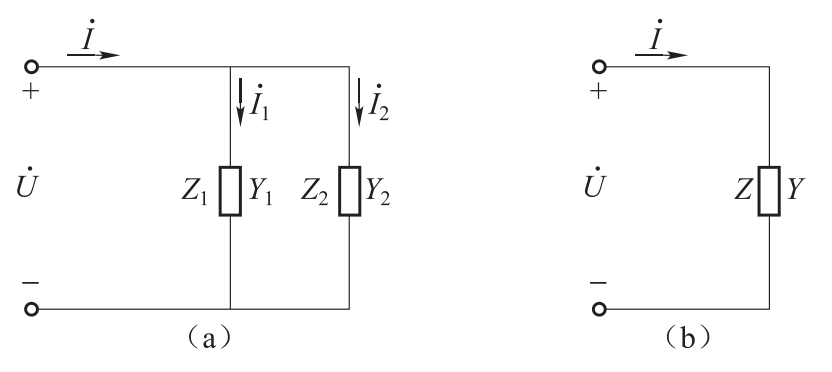
图1.75　阻抗（导纳）并联及其等效电路

（a）阻抗（导纳）并联；（b）等效电路

由于阻抗的串联电路与导纳的并联电路也是互为对偶的电路，根据对偶规则，容易推知该电路具有以下特点：

① 各导纳两端的电压是同一电压。

② 总电流满足以下关系：

式中，Y为电路的等效导纳，等效电路如图1.75（b）所示

③ 等效导纳满足以下关系：

　　Y=Y₁+Y₂　　　　　　　　　　（1.2.76）

即等效导纳等于并联导纳之和，一般当几个导纳并联时：

　　Y=∑Y_K=∑G_K+j∑B_K=|Y|∠θ （1.2.77）

式中，∑B_K中容纳B_C取正号，感纳B_L取负号。

④ 每个导纳中的电流满足以下关系：

注意：一般I≠I₁+I₂，|Y|≠|Y₁|+|Y₂|

练一练

1. 在图1.76所示电路中，已知X_L>X_C，则该电路呈电感性，对不对？

2. 在图1.76中，如果X_L=X_C=2Ω，流过电容的电流为3A，求：

（1）电感中流过的电流。

（2）干路电流。

图1.76　练习图16

七、交流电路中的谐振

前面的分析可知，在正弦交流电路中，一个含R、L、C的无源二端网络，通过阻抗的串、并联等效变换，可用一个等效阻抗或等效导纳来表示，如图1.77所示。

图1.7中：Z=|Z|∠ϕ=R+jX

　　Y=|Y|∠θ=G+jB

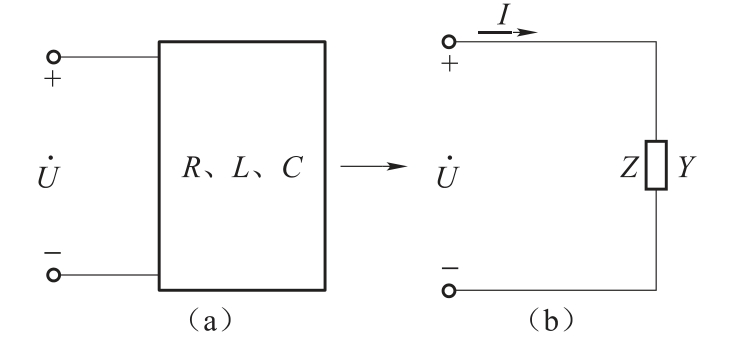
图1.77　含R、L、C的无源二端网络及其等效电路

等效阻抗Z或导纳Y都是ω（或f）的函数，且与电路参数有关，在一定条件下，其虚部X=0（或B=0）时，ϕ=0（或θ=0）电路呈电阻性。此时，电压与电流同相，这种现象称为谐振。谐振是电路的一种特殊的工作状态，在电工和电子技术中得到广泛应用，谐振也可能产生过电压或过电流，造成设备或元件的损坏，又要注意防止。按电路连接的方式不同，谐振分为串联谐振和并联谐振。谐振发生在串联电路中称为串联谐振，发生在并联电路中则称为并联谐振。

（一）串联谐振

在R、L、C串联的电路（图1.65（a））中：

　　Z=|Z|∠ϕ=R+jX=R+j(X_L−X_C)

当其虚部为零，即

　　X_L=X_C（1.2.82）

此时ϕ=0，u与i同相，电路发生串联谐振，式（1.2.82）是发生串联谐振的条件，即

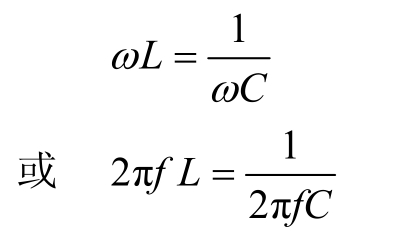
可见，无论改变电路参数L或C，还是改变频率f（或角频率w）都可满足上述谐振条件，使电路发生谐振。谐振角频率和谐振频率分别用ω₀和f₀表示，则得

谐振时的相量图如图1.78所示，串联谐振具有以下特点。

① 电路阻抗模

当发生串联谐振时

此时Z值最小。因此在电压U不变时，电流I最大，此时

② 阻抗角ϕ=0，电路呈电阻性。故有

　　P=UIsinϕ=UI=S

　　Q=UIsinϕ=0

电源供给的能量全被电阻消耗，电源与电路不交换能量，L和C间互换能量，互相补偿。

③ 由相量图可知

　　U_R=U

　　U_L=U_C=I₀X_C=I₀X_C=

当X_L=X_C>R时

　　U_L=U_C>U

由此可以看出，当发生串联谐振时，电感和电容上的电压，可能高于电源电压，故串联谐振又称电压谐振。由于过高的电压可能击穿线圈和电容器的绝缘层，因此在电力系统中应避免发生电压谐振。但在无线电技术中，常利用串联谐振在电容或电感元件两端产生高于信号源几十倍或几百倍的电压。例如，图1.79（a）所示的收音机调谐电路，其等效电路如1.79（b）所示，其中R为调谐线圈的电阻。

图1.78　串联谐振相量图

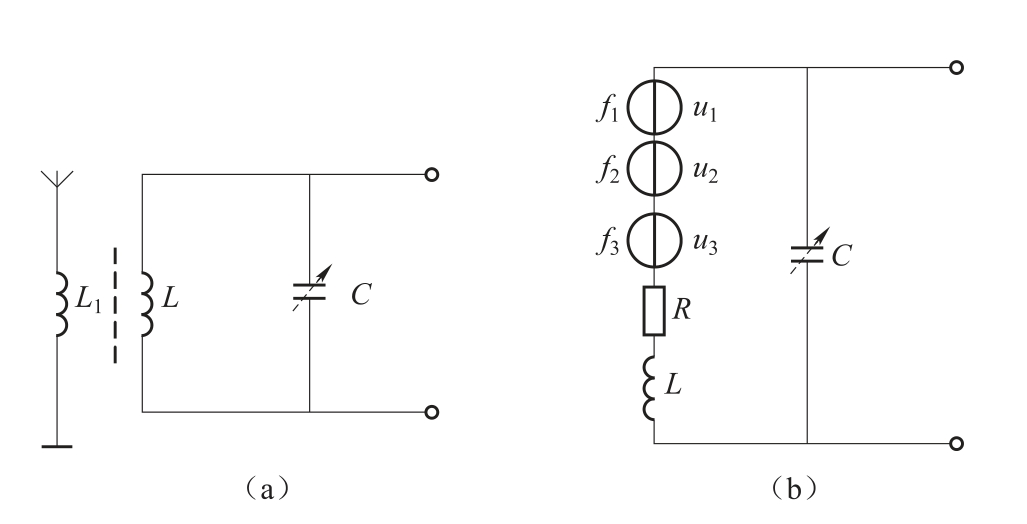
图1.79　收音机调谐电路及其等效果电路

（a）调谐电路；（b）等效电路

天线线圈L₁接收到的各种不同频率的信号，在调谐线圈中感应出不同频率的信号源电压u₁，u₂，u₃，…。调节可变电容器C，对所需信号频率发生串联谐振。此时LC调谐电路中该频率的电流最大，电容两端的电压也最大，经放大器进一步放大后，从而起到选择收听该频率电台广播的目的。

在无线电技术中，谐振电路选择性的好坏用品质因数Q来衡量，它的定义为

品质因数Q值越大，选择性越好。想一想处于谐振状态的R、L、C串联交流电路中，若增大频率，则电路将呈现出什么性？

（二）并联谐振

在R、L、C并联电路（图1.70（a））中：

　　Y=|Y|∠θ=G+jB=G+j(B_C−B_L)

当其虚部为零，即

　　B_C=B_L　　　　　　　　　　　（1.2.84）

此时，θ =0，u与i同相，电路发生并联谐振。式（1.2.84）是发生并联谐振的条件，即

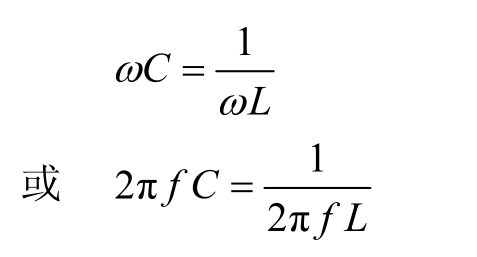
谐振频率

图1.80　并联谐振相量图

谐振时的相量图如图1.80所示，可见，该电路的谐振条件和谐振频率公式与R、L、C串联电路相同。前面已经提到，R、L、C串联电路与R、L、C并联电路是互为对偶的电路，故在两个电路中发生的串联谐振和并联谐振，也是互为对偶的两种电路工作状态。根据对偶原理可知并联谐振有如下特点：

① 电路的导纳模在发生并联谐振时

其值最小（即阻抗模最大）。在电流I不变时，电压U最大，此时

② 导纳角θ =0，电路呈电阻性，故有

　　P=UIcosθ=UI=S

　　Q=UIsinθ=0

③ 由相量图可知I_R=I

当B_C=B_L>G时，

这就是说，并联谐振时，电容和电感支路电流，可能大于总电流，故并联谐振又称电流谐振。

并联谐振在电子技术中也有广泛的应用。

想一想　　比较串、并联谐振电路，它们有什么相同和不同之处？

八、功率因数的提高

通过前面的分析，已知交流电路的有功功率的大小不仅取决于电压和电流的有效值，而且和电压、电流间的相位差 ϕ 有关。即

　　P=UIcosϕ

cosϕ为电路的功率因数，它与电路的参数有关。纯电阻电路cosϕ=1，纯电感和纯电容的电路cosϕ=0。一般电路中，0<cosϕ<1。目前，在各种用电设备中，除白炽灯、电阻炉等少数电阻性负载外，大多属于电感性负载。例如工农业生产中广泛使用的三相异步电动机和日常生活中大量使用的日光灯、电风扇等都属于电感性负载。而且它们的功率因数往往比较低。功率因数低，会引起下列两个问题。

第一，降低了供电设备的利用率。

供电设备的额定容量S_N=U_NI_N是一定的，其输出的有功功率为

　　P=U_NI_Ncosϕ=S_Ncosϕ

当cosϕ=1时，P=S_N，供电设备的利用率最高；一般cosϕ<1，P<S_N；cosϕ越低，则输出的有功功率P越小，而无功功率Q越大，电源与负载交换能量的规模越大，供电设备所提供的能量就越不能充分利用。

第二，增加了供电设备和线路的功率的损耗。负载从电源取用的电流为：

在P和U一定的情况下，cosϕ越低，I就越大，供电设备和输电线路的功率损耗就越大。因此，提高电路的功率因数就可以提高供电设备的利用率和减少供电设备和输电线路的功率损耗，具有非常重要的经济意义。

感性负载

通常情况下，一般把带电感参数的负载，即符合电压超前电流特性的负载，称为感性负载。通俗地说，感性负载是应用电磁感应原理制作的大功率电器产品，如电动机、压缩机、继电器、日光灯等。

提高电路的功率因数的方法是在感性负载两端并联电容器，如图1.81（a）所示。以电压为参考相量，可画出其相量图，如图1.81（b）所示。

资料卡

由图1.81可知，并联电容前，电路的电流为感性负载的电流，电路的功率因数为感性负载的功率因数1cosϕ；并联电容后，电路的总电流。电路的功率因数变为cosϕ。可见，并联电容器后，流过感性负载的电流及其功率因数没有变，而整个电路的功率因数1coscosϕϕ>，比并联电容前提高了；电路的总电流1II<，比并联电容前减少了。这是由于并联电容器后感性负载所需的无功功率大部分可由电容的无功功率补偿，减小了电源与负载之间的能量交换。但要注意，并联电容后，电路的有功功率并未改变。根据相量图可得