小净距隧道位移反分析与探讨

小净距隧道位移反分析与探讨

靳晓光¹　秦　峰²　陈少华²

（1重庆大学土木工程学院　重庆　400030；2重庆交通科研设计研究院　重庆　400067）

摘　要　结合京福高速公路南洲Ⅰ号隧道Ⅴ级和Ⅳ级围岩段监控量测资料，采用单纯形法、阻尼最小二乘法、遗传算法、遗传模拟退火法、混合遗传算法等对Ⅴ，Ⅳ级围岩E，C进行了反分析。结果表明，不同方法反分析得到的结果有一定甚至较大的差距，反分析精度的高低与围岩级别、位移量及位移变化过程有关。因此，进行隧道位移反分析时应采用几种方法，选择反分析精度最高者为采用的方法。

关键词　小净距隧道　监控量测　位移反分析

位移量是描述物体受力变形性态的一类重要物理量，目前已被用作反演确定初始地应力和地层材料特性参数的主要依据。自20世纪70年代初由Karanagh等（1971年）提出反分析方法后，随之Sakurai（1974年），Gioda（1980年），Kirgtem（1991年）等相继用数值方法和解析方法开展了研究和应用。我国学者大体上是20世纪80年代开始在岩石地下工程的参数和地应力推求方面进行应用研究的。其中我国学者杨志法（1981年）、冯紫良、杨林德（1983年）、郭怀志等（1983年）、张有天等（1984年）、朱维申等（1985年）、王建宇（1986年）等人用不同方法做了多方面的研究工作。

位移反分析方法可分为正反分析法和逆反分析法两类。逆反分析法是正反分析法的逆过程，计算过程简单，但须先建立求逆公式和编制相应的程序，适用性差。正反分析法是正分析计算的优化逼进过程，一般通过不断修正未知数的试算值逼进和求得优化解，计算机运作时间虽长，但可利用原有正算程序进行计算，便于处理各种类型的反分析问题，并可用于各类非线性问题的分析，适用性强。这里应用同济曙光软件，根据小净距隧道现场监控量测资料，按上下台阶法施工，应用单纯形法、阻尼最小二乘法、遗传算法等，对Ⅴ，Ⅳ级围岩物性参数（E，C）进行反分析计算。

1　位移反分析方法

反分析方法是根据现场实测的位移值，计算地应力和材料性质等参数，可采用解析法、有限元等方法以及弹性、弹塑性等本构模型进行求解［1-3］。

隧道开挖后引起的围岩位移可由各初始应力分量在独立作用的情况下产生的位移量叠加而得。设某任意测点由各初始应力分量产生的位移为U_i（i＝1，2，…，n），n为初始应力分量数。如该测点由隧道开挖引起的总位移为U^*，则有：

在反分析问题中，因初始地应力分量为未知量，故U_i亦为未知数。但U^*为可通过现场量测采集的已知量。

设初始地应力分量为｛P｝，并设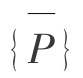为单位初始应力分量，则可写出：

式中，［A］为应力系数矩阵。因为已知量，故由反演计算确定初始地应力｛P｝的问题可归结为求算应力系数A_i（i＝1，2，…，n）的问题。

设u_i（i＝1，2，…，n）为由各单位应力分量产生的测点位移，则各测点由各应力分量引起的测点位移可表示为：

其中，u_i为已知量。将式（3）代入式（1），可得：

因式中U^*为已知测点位移，故式（4）可用于建立在算出u_i值后求解A_i值的方程组。

对每个测点都可写出一个形如式（4）的方程。

如采集位移信息的测点总数为m，则可得如下的量测方程组：

当量测信息总数等于未知数总数（m＝n）时，即可解得A_i。

为使计算结果有更高的精度，还可多测一些测点m＞n，以消除误差。用最小二乘法原理来估计最可置信的应力系数A_i。

设m个测点的位移实测值，由于种种误差的存在，每一个都与其真实值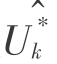有所偏离，记总偏差为s，则有

为了得到使总偏差为最小的一组荷载系数A_i，应使式（7）得到满足：

将式（5）代入式（7）得：

即可写成：

其中，

图1　南洲Ⅰ号隧道进口

2　监控量测资料分析

2．1　Ⅴ级围岩

南洲Ⅰ号隧道（如图1所示）ZK175＋430断面为Ⅴ级围岩，拱顶下沉和周边收敛量测资料，如图2和图3所示。量测结果显示，该断面最大沉降为39．0 mm，单侧最大收敛6．0 mm。

图2　南洲Ⅰ号隧道ZK175＋430断面拱顶沉降

图3　南洲Ⅰ号隧道ZK175＋430断面周边收敛

2．2　Ⅳ级围岩

Ⅳ级围岩位移反分析采用南洲Ⅰ号隧道ZK175＋450断面拱顶下沉和周边收敛量测资料，如图4和图5所示。量测结果显示，该断面最大沉降为10．35 mm，单侧最大收敛5．9 mm。

图4　南洲Ⅰ号隧道ZK175＋450断面拱顶沉降

图5　南洲Ⅰ号隧道ZK175＋450断面周边收敛

3　隧道位移反分析

3．1　Ⅴ级围岩

Ⅴ级围岩位移反分析采用南洲Ⅰ号隧道ZK175＋430断面监控量测资料。弹塑性位移反分析模型如图6所示，锚杆支护范围看作一种材料，锚杆材料和间距对隧道围岩的作用通过在计算中采取施锚区岩体弹性模量和粘聚力提高的办法予以反映（孙钧，1996年）。具体计算公式为：

式中，E_b，C_b分别为施锚区岩体弹性模量和粘聚力；E，C分别为未施锚区岩体弹性模量和粘聚力；τ_b为锚杆抗剪强度；e，i分别为锚杆环向和纵向间距。

图6　Ⅴ，Ⅳ级围岩位移反分析结构模型

Ⅴ级围岩E，C位移反分析遗传算法分析结果为：

单纯形法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（1，1）　2058000．0000　2785612．8778

2 AMT（1，4）　　　126．0000　　　186．8533

阻尼最小二乘法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（1，1）　2058000．0000　2058000．0000

2 AMT（1，4）　　　126．0000　　　126．0000

遗传算法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（1，1）　2058000．0000　2183094．1176

2 AMT（1，4）　　　126．0000　　　167．7529

遗传模拟退火法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（1，1）　2058000．0000　2941729．4118

2 AMT（1，4）　　　126．0000　　　106．4824

混合遗传算法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（1，1）　2058000．0000　2618905．8824

2 AMT（1，4）　　　126．0000　　　167．7529

可以看出，阻尼最小二乘法模拟结果最好。

3．2　Ⅳ级围岩

Ⅳ级围岩位移反分析采用南洲I号隧道ZK175＋450断面监控量测资料。Ⅳ级围岩E，C反分析结果发现，遗传算法反分析结果较为接近，其结果为：

单纯形法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（6，1）　8619000．0000　9151974．7082

2 AMT（6，4）　　　378．0000　　　456．0000

阻尼最小二乘法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（6，1）　8619000．0000　9151974．7082

2 AMT（6，4）　　　378．0000　　　386．0000

遗传算法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（6，1）　8619000．0000　9151974．7082

2 AMT（6，4）　　　378．0000　　　380．6141

遗传模拟退火法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（6，1）　8619000．0000　9151974．7082

2 AMT（6，4）　　　378．0000　　　366．4824

混合遗传算法：

*INITIAL、BACK-ANALYSIED VALUE*

1 AMT（6，1）　8619000．0000　9151974．7082

2 AMT（6，4）　　　378．0000　　　427．7500

可以看出，由于受多因素的影响（如位移量测值、反分析模型及算法等），围岩体弹性模量误差相对较小，内聚力误差较大。

4　结论和建议

单纯形法、阻尼最小二乘法、遗传算法、遗传模拟退火法、混合遗传算法等不同方法反分析得到的结果有一定甚至较大的差距，反分析精度的高低与围岩级别、位移量及位移变化趋势有关。因此，进行隧道位移反分析时应采用几种方法进行综合比较，选择反分析精度最高者为采用的方法。

参考文献

［1］吴鸿庆，任侠．结构有限元分析［M］．北京：中国铁道出版社，2000．

［2］赵冰，喻小明．一种基于有限元线法的位移反分析方法［J］．长沙交通学院学报，2001（1）：11-13．

［3］孙其清，赵万强，高峰，等．乌鞘岭隧道F4断层支护结构位移反分析［J］．铁道工程学报，2008（2）：50-53．