游动方位惯导系统导航参数的计算

3.2.4　游动方位惯导系统导航参数的计算

当地水平坐标系通常包括地理坐标系Ox_g y_g z_g(东北天)和自由方位坐标系及游动方位坐标系Ox_w y_w z_w，如图3-4所示。

图3-4　地平坐标系

地理坐标系在惯性空间既跟踪地球的自转也跟踪载体运动所形成的绕地心的转动，即在惯性空间转动的角速度为:

在不考虑地球为椭球的情况下，有:所以，在指北方位惯导系统中，需要按式(3-8)给平台施加指令角速度，使平台跟踪地理坐标系在惯性空间的转动。由于tan L的发散性，在高纬度地区，沿垂直轴的施矩速度很大，物理上难以实现，为避免这一困难，常采用自由方位或游动方位坐标系。

自由方位坐标系在方位上稳定在惯性空间，该坐标系相对地球有一方位角α_f，

游动方位坐标系沿垂直轴只跟踪地球自转角速度ω_ie sin L。类似于自由方位坐标系情况，该坐标系相对地球有一游动方位角α，

载体航向角ψ和平台航向角ψ_p的关系为:

由于在垂直方向去掉了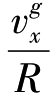 tan L项的跟踪速度，因而克服了在指北方位惯导系统中施矩太大的困难。

以下介绍游动方位惯导系统各导航参数的计算方程。

1.位置计算

若以地球坐标系Ox_e y_e z_e为初始位置，则:

(1)绕z_e轴转动(λ+ 90°)角，得到Ox'y'z';

(2)再绕x'轴转动(90°－L)角，得到Ox_g y_g z_g;

(3)再绕z_g轴转动α角，则可得到游动方位坐标系Ox_w y_w z_w。

根据以上变换，可以求得游动方位坐标系ω到地球坐标系e之间的转换矩阵。

根据c_ij可得到:

纬度L的定义域为(－90°，+ 90°)，所以L的主值即真值。由于λ的定义域为(－180°，+ 180°)，α的定义域为(0，360°)，故还需根据c₁₃符号、λ_主符号以及c₃₂符号、α_主符号，来分别判断λ和α所存在的象限，并得到λ真值和α真值。

在式(3-12)中，位置矩阵的元素可通过解矩阵微分方程来得到。矩阵微分方程为:

考虑到游动方位= 0，则矩阵微分方程展开得:

前三个方程和后边的六个方程无关，故可独立求解后六个方程。再利用矩阵正交约束条件，求解前三个方程。由于位置计算只用到c₁₃，故只求c₁₃即可。

故，按正交条件则有:

初始条件由L₀，λ₀，α₀确定。

2.角速度的计算

游动方位坐标系= 0，

式中，子午圈内的曲率为:

而卯酉圈内的曲率为:

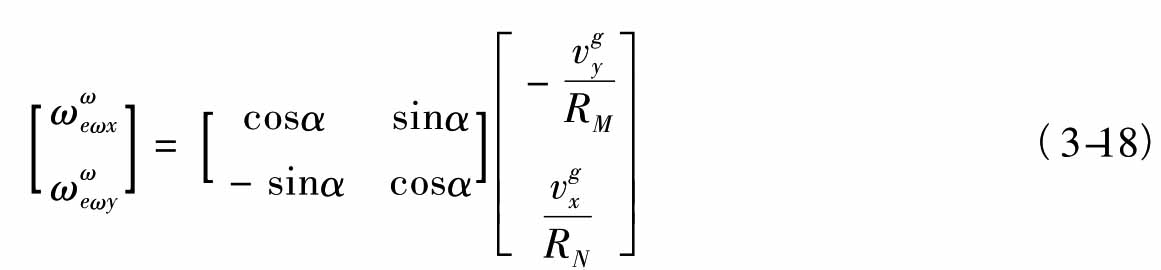
将式(3-19)～式(3-21)代入式(3-18)得:

若设

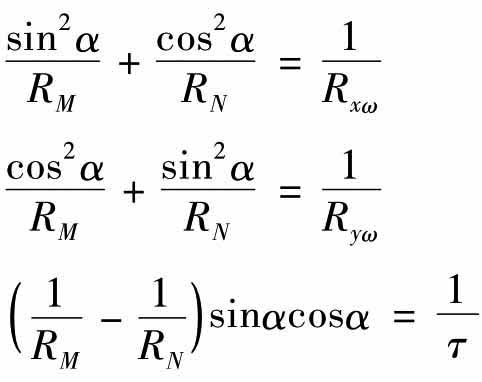
则有

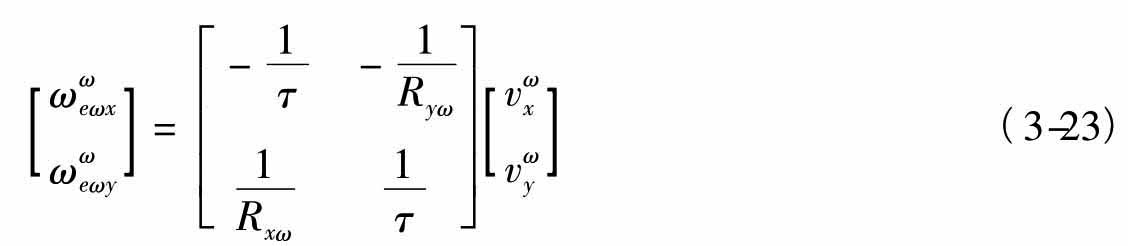
式中R_xω，R_yω分别为游动方位坐标系x_ωz_ω和y_ωz_ω平面的等效曲率半径;τ为扭曲率。

自此，实现了角速度的计算。

3.速度v计算

由比力方程可得速度微分方程:

式中

分解形式为

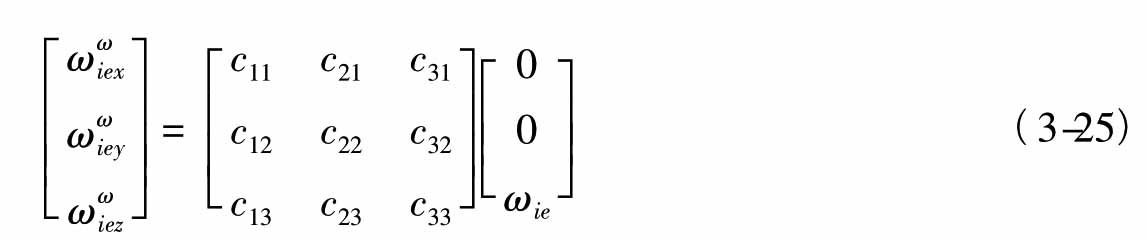
考虑到游动方位坐标系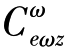= 0，则式(3-24)展开式为:

由于惯导系统的垂直通道是不稳定的，因此不能按式(3-26)单独积分计算，通常需要引入外部高度信息进行组合。如果载体垂直速度不大，可略去，只考虑平面导航，则式

(3-26)可简化为:

4.平台指令角速度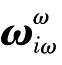计算

平台指令角速度ω^ω

iω为:

分解式为:

或