任务一 资金的时间价值
知识目标
●掌握现值、年金和终值等相关名词的含义。
●掌握资金时间价值的计算公式。
能力目标
●能够运用资金时间价值理论，进行车辆净年金收入、现值成本等项目的计算。
任务剖析
对于一辆车来说，发生在车辆营运年限内的费用和收入等项目，是不能直接进行相关加减运算的。这样为了进行精确的运营情况的分析，要利用资金时间价值的理论来进行计算。
资金时间价值理论是指把不同时点发生的现金流通过合适的方法换算成同一时点的现金流，这样进行加减运算就变得更为科学和合理。对于车辆这种较长时间段的投资来说，进行科学的分析，不利用资金时间价值来进行评价，最终的结论就会欠妥当。
任务载体
对于资金时间价值的含义对很多初学者来说是比较困难的。那我们通过几个例子来体会一下：
【例1】设年初一项购买旧机动车投资为10万元，年末成为15万元。另外一项购车投资也是10万元，年末成为12万元。显而易见前者比后者赚取利润要大，更有吸引力。
【例2】两项购买旧机动车投资均为10万元的投资，一项在第一年末得11万元，另一项在两年后也得11万元。显然，第一项投资比第二项投资更有吸引力。也就是说，资金收回越早则效益越高。
【例3】现有两项购买旧机动车投资计划，一项投资为10万元，年末收入12万元。另一项投资20万元，两年后收入为25万元。仅从净收入来看，后一项比前一项更有利。然而，若考虑资金的时间价值，则最好的方案则取决于利率，而不是绝对收入。
【例4】考虑两项均为10万元购买旧机动车投资的方案，第一项于年末可得12万元，而另一项于第二年末可得13万元。我们不能只凭两个计划的净收入的差别就认定后一项比前一项好。因为利率、投资的时间及收益的大小都将影响其效益。
相关知识
1．1．1 相关概念
在进行资金时间价值在车辆营运过程中产生的费用和收入等相关项目的评价的时候，必须要学习收益、现值、终值、年金、折现率和时间等概念。
1．1．1．1 收益
收益是指净收益流量，即现金流入量减去现金流出量。它尚未扣除投资的资本成本。表现收益大小的方式有两种：
（1）收益的数额或金额。如一辆从事营运的汽车，一年内净收入10万元，10万元就是这辆汽车的收益数额。
（2）收益率。收益率是指收益数额对投资数额的比率。它表明每元投资所得的收益。收益多少和投资大小有关。为了比较各项投资收益的大小，用收益率作标准。
收益率＝收益÷资本
1．1．1．2 现值
现值通常以字母P表示。它是指发生在（或折算为）某一特定时间序列起点的现金流量。
1．1．1．3 终值
终值也称未来值或将来值，通常以字母F表示。它是指发生在（或折算为）某一特定时间序列终点的现金流量。
1．1．1．4 年金
年金又称为等额序列值。通常以字母A表示。它是指发生在（或折算为）某一特定时间序列各时间期末（不包括零期）并且金额大小相等的现金流量序列，也常称年金。
1．1．1．5 折现率
折现率通常用字母i表示。在经济分析中如果不作其他说明，一般指年利率或收益率。
1．1．1．6 时间
这里的时间是指在等值计算中计算时间价值的期数，通常以年来计。
1．1．2 资金时间价值的计算公式
1．1．2．1 现值与终值的变换公式
1．已知现值、折现率和时间求终值
已知现值P、折现率i和时间n，求终值F。
则有n期末的终值F与现值P的关系为
F＝P（1＋i）n
简记为
F＝P（F／P，i，n）
式中：（1＋i）n为终值系数，记为（F／P，i，n），其值可通过查普通复利系数表求得。括号中斜线上的符号表示所求的未知数，斜线下的符号表示已知数。系数符号（F／P，i，n）表示已知P、i、n求F。
2．已知终值、折现率和时间求现值
已知终值F、折现率i和时间n，求现值P。
则有现值P与n期末的终值F的关系为
简记为
P＝F（P／F，i，n）
式中：
为一次支付现值系数，简称贴现系数。系数符号（P／F，i，n）表示已知F、i、n求P。
1．1．2．2 年金与终值的变换公式
1．已知年金、折现率求终值
已知每年现金流量A（年金）、折现率为i，求在n年内积累的资金总量F。则年金A与终值F的关系为
简记为
F＝A（F／A，i，n）
式中：
为等额序列终值系数。系数符号（F／A，i，n）表示已知A、i、n，求F。
2．已知终值、收益率求年金
为了在n年内累积资金F、收益率为i，求每年的积累资金A。即已知终值F、折现率i、时间n，求年金A，则有
简记为
A＝F（A／F，i，n）
式中：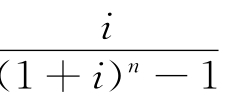
为等额序列偿债基金系数。系数符号（A／F，i，n）表示已知F、i、n，求A。
1．1．2．3 年金与现值的变换公式
1．已知现值、折现率和时间求年金
现在投资金额为P、折现率为i，要求在n年内全部收回投资，求每年收回的资金A。即已知现值P、折现率i和时间n，求年金A，则有
简记为
A＝P（A／P，i，n）
式中
为资金回收系数。系数符号（A／P，i，n）表示已知P、i、n，求A。
2．已知年金、折现率和时间求现值
已知折现率为i，n年内每年回收A元，求现在的投资P。即已知年金A、折现率i、时间n，求现值P，则有
简记为
P＝A（P／A，i，n）
式中：
为等额序列现值系数。系数符号（P／A，i，n）表示已知A、i、n，求P。
现将各公式及系数数列于下表。各系数值在具体计算时可通过查表取得。
1．1．2．4 计算举例
【例1】某单位欲购置一辆汽车从事营运业务。该车辆的剩余使用寿命为6年，购置全价为80 000元。据预测，该车辆在使用过程中，每年的总费用支出为20 000元，每年总收入为60 000元。假定折现率10%，试在将车辆的购置全价折算为剩余使用期限内的年金的前提下，估算该车每年的净年金收入。
根据分析可知，这是一个已知现值，求年金的问题。
据已知条件可知：折现率i＝10%；时间n＝6年；现值P＝80 000元
由现值折算成年金为
A＝80 000元×（A／P，10%，6）
＝80 000元×0．229 61
≈18 368元
上式中（A／P，10%，6）的值可通过查表取得，为0．229 61。
由于车辆的年收入为60 000元，年费用支出为20 000元，故该车的净年金收入为
60 000元－20 000元－18 368元＝21 632元
【例2】某单位欲购置一辆汽车从事营运业务。该车辆的剩余使用年限为6年，购置全价为80 000元。据预测，该车辆在使用过程中年耗油费用为10 000元左右、年维护费用为5 000元左右、其他管理费用为10 000元左右，假定折现率为10%，试估算该车辆的现值成本。
根据分析可知，这是一个已知年金，求现值的问题。
据已知条件可知：折现率i＝10%；时间n＝6年。
车辆每年所需费用合计为
10 000元＋5 000元＋10 000元＝25 000元
即年金A＝25 000元。
由年金折算成现值为
P＝25 000元×（P／A，10%，6）
＝25 000元×4．355 26
＝108 882元
由于购置车辆时，一次性投资为80 000元，故车辆的现值成本为
80 000元＋108 882元＝188 882元。
任务回顾
（1）资金时间价值理论是分析较长时间段投资的有效方法。
（2）对于单辆车来说，需要计算评价的项目很多。需要分析是计算哪种我们常见概念（成本、净收入）的资金时间价值的含义（现值、终值、年金）。
任务实施步骤
（一）任务要求
计算一营运车辆的成本现值、成本年金、成本终值和净收入现值、净收入年金。
（二）任务实施的步骤
营运车辆的单方面评价可参考下面的步骤：
（1）车辆情况调查，车辆购买费用、车辆年费用、车辆年收入、车辆剩余使用年限；
（2）经济环境分析，找出合适的折旧率；
（3）根据所求项目进行相关计算分析。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
