四面体单元

2.2.2　四面体单元

1）矩阵［B］

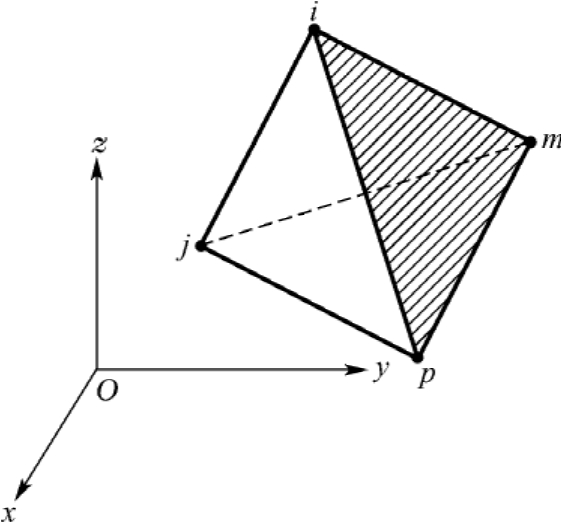
图2.9　常应变四面体单元

如图2.9所示的一个四面体单元，以4个角点i、j、m、p为结点。这是最早提出的、也是最简单的空间单元。

每个结点有3个位移分量：

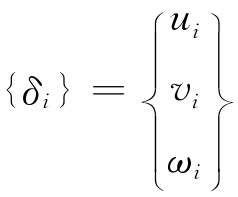
每个单元共有12个结点位移分量，可表示为一个向量：

｛δ｝^e＝［δ_iδ_jδ_mδ_p］^T

假定单元内任一点的位移分量是坐标的线性函数：

以i、j、m、p结点的坐标代入上式，可求得12个系数β₁～β₁₂，再回代入上式，可得

其中

式中　V——四面体ijmp的体积。

为了使四面体的体积V不致成负值，单元结点的标号i、j、m、p必须按照一定的顺序。在右手坐标系中，当按照i→j→m的方向转动时，右手螺旋应向p的方向前进，如图2.9所示。

在空间问题中，每个结点具有6个应变分量。由弹性力学可知，应变矩阵可定义如下：

将式（2－60）代入上式，得到

｛ε｝＝［B］｛δ｝^e＝［B_i－B_jB_m－B_p］｛δ｝^e　　　　　　　　　　　　　　　（2－65）

子矩阵［B_i］是如下的6×3矩阵：

由于矩阵［B］中的元素都是常量，单元应变分量也都是常量。

由式（2－59）和式（2－64）可知，式（2－59）中系数β₁、β₅、β₉代表刚体移动，β₂、β₇、β₁₂代表常量正应变；其余6个系数反映了常量剪应变和刚体转动。因此，式（2－59）中12个系数充分反映了单元的刚性位移和常量应变。

2）弹性矩阵［D］

对于各向同性体，弹性矩阵［D］决定于下式：

3）四面体单元的单元刚度矩阵

将矩阵［B］的表达式（2－66）代入式（2－45），可求出单元刚度矩阵［k］。由于矩阵［B］的元素是常量，计算是简便的。计算公式如下：

［k］＝［B］^T［D］［B］V

或

子矩阵［k_rs］由下式计算：

［k_rs］＝［B_r］^T［D］［B_s］V

对于各向同性体

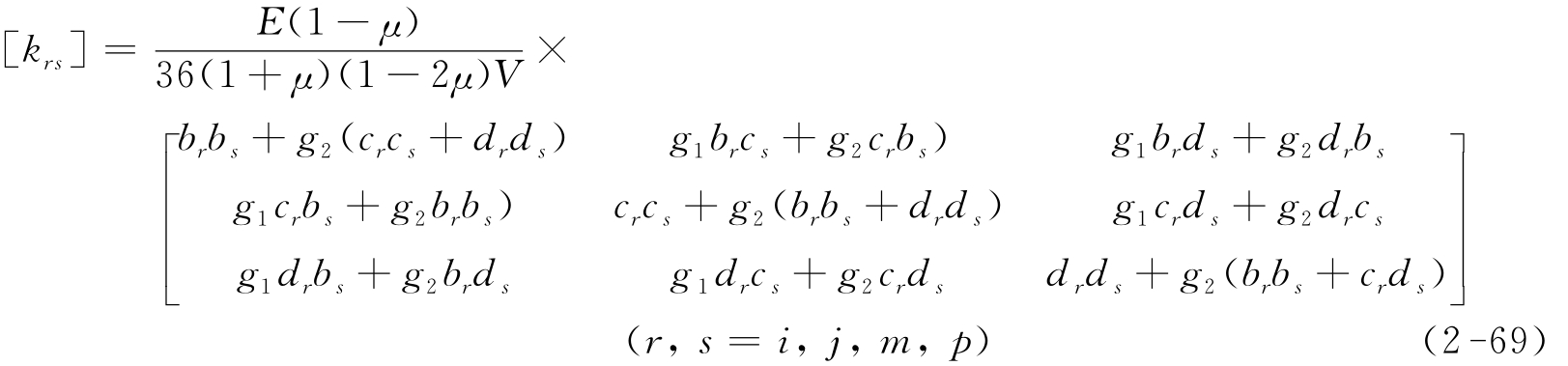
其中：g₁＝

4）四面体单元的结点载荷

下面用虚位移原理推导各种结点载荷算式。

（1）分布体积力

设单位体积内承受的体积力为

当单元中发生虚位移｛r^＊｝时，体积力｛q｝所做的功为

它应该等于等效结点载荷所做的功，即

由于虚位移｛δ^＊｝是任意的，由上式可得体积力｛q｝的等效结点载荷如下：

上式右边的重积分应当在单元e的整个体积内进行。

对于四面体单元而言，可求得i点的结点载荷如下：

式中　V——单元体积。

也就是说，3个方向的体积力都平均分配到单元的4个结点上。

（2）分布面力

设单元e是靠近边界的单元，其在边界S上作用着分布的面力｛p｝：

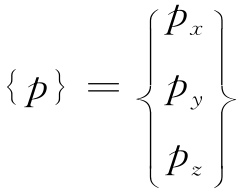
当单元中发生虚位移｛r^＊｝＝［N］｛δ^＊｝^e时，面力｛p｝所做的功为

它必须等于等效结点载荷所做的功，由此得到

上式右边的面积分是在分布载荷所作用的表面S上进行的。

对于四面体单元而言，如果其边界面ijm上作用着面力｛p｝，在结点i、j、m上的集度分别为，则可求得结点载荷如下：

式中　A_ijm——边界表面ijm的面积。