2.5.2 典型的一维、二维和三维形函数
1)一维形函数
对于如图2.11所示的一维杆单元(一维母单元),采用坐标ξ(局部坐标),-1≤ξ≤+1。通过坐标变换,可以得到整体坐标系(x,y,z)中不同长度和形状的曲线单元(子单元)。一维形函数如下:

图2.11 一维母单元
(1)线性单元(2结点)
![]()
(2)二次单元(3结点)
![]()
(3)三次单元(4结点)

2)二维形函数
二维母单元是(ξ,η)平面中的2×2正方形,其中
-1≤ξ≤+1, -1≤η≤+1
如图2.12所示,坐标原点位于单元形心上。单元边界由4条直线确定:ξ=±1,η=±1,结点数目应与形函数阶次相适应,以保证用形函数定义的未知量在相邻单元之间的连续性。对于线性、二次、三次形函数,单元每边应分别有2、3、4个结点。除了4个角点外,其他结点放在各边的二等分或三等分点上。二维形函数如下:
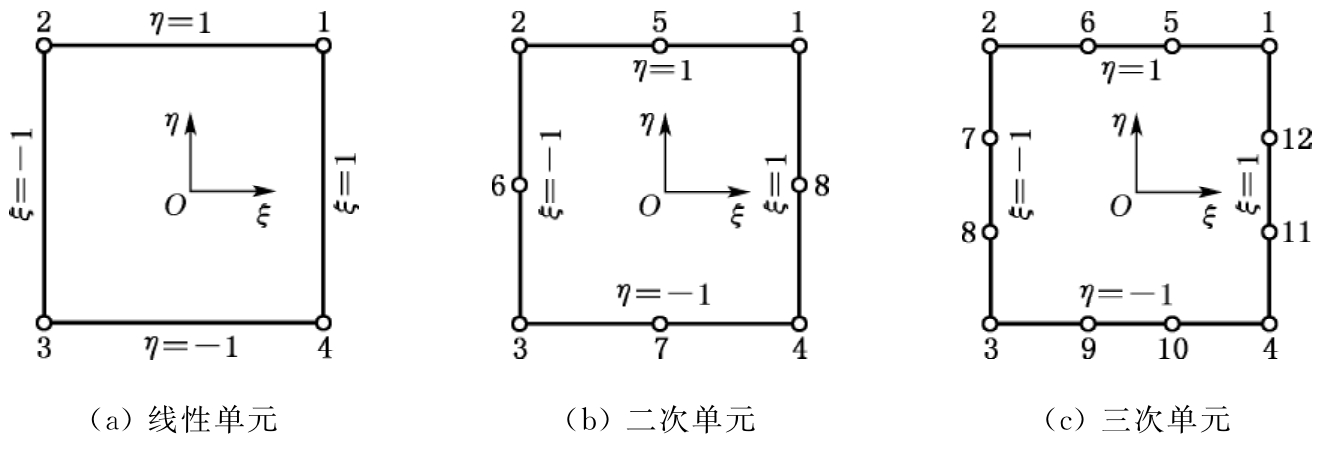
图2.12 二维母单元
(1)线性单元(4结点)
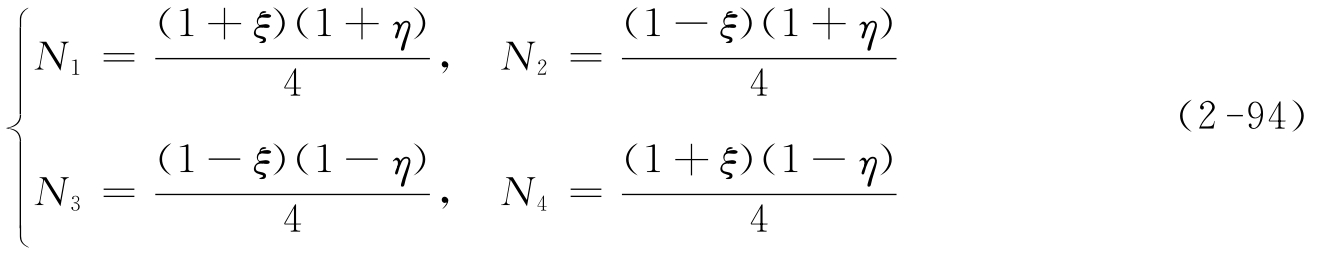
上式也可以合并为下列形式:

式中 ξi、ηi——结点i的坐标。
显然,在单元的4条边界上,形函数是线性的。
(2)二次函数(8结点)
角点:
![]()
边中点:

在单元的4条边上,形函数是二次函数。
(3)三次单元(12结点)
角点:
![]()
边三分点:
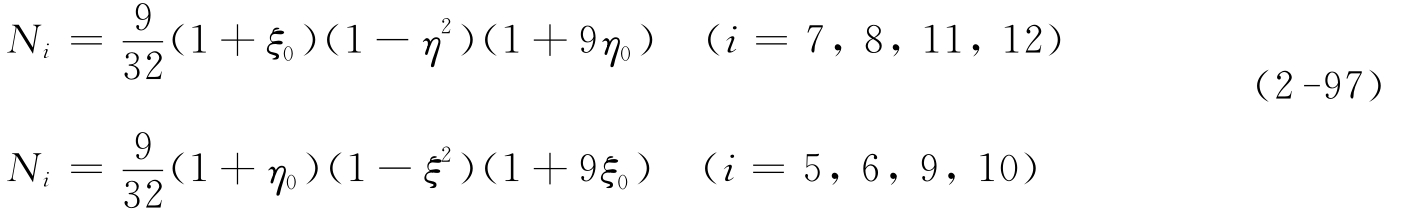
在单元的4条边上,形函数是三次函数。
3)三维形函数
三维母单元是(ξ,η,ζ)坐标系中的2×2×2正六面体,其中:
-1≤ξ≤+1, -1≤η≤+1, -1≤ζ≤+1
如图2.13所示,坐标原点在单元形心上,单元边界是6个平面:ξ=±1,η=±1,ζ=±1。单元结点放在角点及各棱的等分点上。三维形函数如下:

图2.13 三维母单元
(1)线性单元(8结点)
![]()
(2)二次单元(20结点)
角点:
![]()
典型边中点:

(3)三次单元
角点:
![]()
典型边中点:
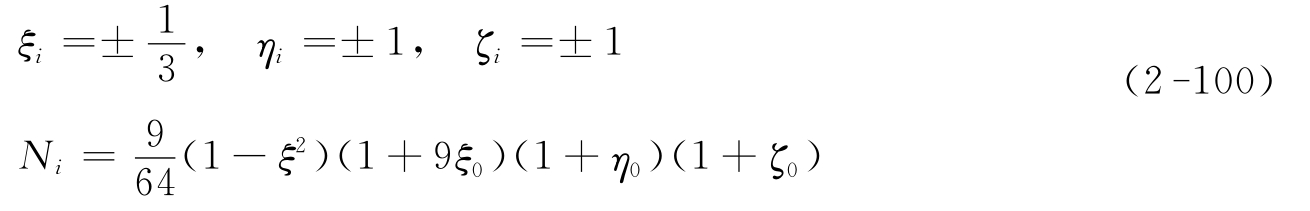
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















