修正模型用户子程序的编写

4.3.3　修正Burgers模型用户子程序UMAT的编写

1）蠕变的有限元实现

与弹塑性分析相似，在当前的大多数研究中，是将单轴试验中观察到的规律，通过试验与推理将它推广至多维状态。金属蠕变表明，与塑性应变相同，蠕变由应力偏量产生，而静水压力起的作用很小。因此，可以将塑性理论的一些方法推广至蠕变的情况，例如Von Mises理论和Tresca理论。现用Von Mises的等效应变和等效应力代替式（4－26）中的单轴蠕变本构方程中的应力与应变，就得到多维应力情况下的蠕变本构关系式（4－27）：

ε^c＝a₀σ^a₁t^a₂　　　　　　　　　　　　　　　（4－26）

式中　a₀、a₁、a₂——材料常数。

通过测量不同温度下的这3个常数来考虑温度对蠕变应变的影响。

式中　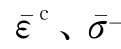——分别表示等效蠕变应变和等效蠕变应力。

对于蠕变应变与应力之间的关系，假定流动定律依然成立，即

式中　f——与塑性理论相似的加载曲面。

将式（4－28）写成率的形式为

将式（4－29）代入等效蠕变应变表达式，再根据等效应力公式可以推出：

则

所以

因此，式（4－29）在Von Mises准则情况下为

对于与时间相关的非线性问题，当前还不能像与时间无关的弹塑性那样，找到一个应力与总应变之间的材料本构矩阵。处理的方法则是采用初应力或初应变法，即把非弹性应变增量当作各增量步开始时的初应变，把初应变对应的应力由虚功原理等价到有限元结点上，构成一项载荷。具体步骤如下：

总应变增量可以写为

｛Δε｝＝｛Δε^e｝＋｛Δε^p｝＋｛Δε^c｝＋｛Δε^T｝　　　　　　　　　　　　　　　（4－33）

式中　｛Δε｝、｛Δε^e｝、｛Δε^p｝、｛Δε^T｝——分别为总应变增量、弹性应变增量、塑性应变增量、蠕变应变增量和温度应变增量。

应力增量可写为

｛Δσ｝＝［D_e］（｛Δε｝－｛Δε^p｝－｛Δε^c｝－｛Δε^T｝）＝［D_e］（｛Δε｝－｛ε₀｝）　　　　　　　　　　　　　　　（4－34）

式中　｛ε₀｝——初应变。

｛ε₀｝＝｛Δε^p｝＋｛Δε^c｝＋｛Δε^T｝　　　　　　　　　　　　　　　（4－35）

在没有塑性应变和温度应变的情况下，只有蠕变应变为初应变。根据虚功原理，从式（4－41）可得到有限元方程为

［K］｛Δu｝＝｛ΔR｝＋｛ΔP₀｝　　　　　　　　　　　　　　　（4－36）

其中　［K］——弹性刚度矩阵；

　　　｛Δu｝——位移增量；

　　　｛ΔR｝——外载荷增量及不平衡力的合力；

　　　｛ΔP₀｝——初应变引起的初应力增量。

显然，初应力增量并不是已知数，而是非线性应变的函数，也即是位移的函数，在求解之前未知。因此，式（4－36）是非线性方程。其求解方法与弹塑性问题相似，将载荷时间函数按时间分成若干段，按时间段逐个加载荷。不同之处在于弹塑性问题与时间无关，而蠕变却是真实的时间。其蠕变应变增量与时间相关，因而，初应力也与时间相关。

2）瞬态温度场下蠕变求解方法

在环境因素的影响下，实际路面结构的温度随着路面深度和时间时刻发生着变化，其温度场是瞬态温度场。作为路面材料的沥青混合料，其材料特性受温度影响很大，材料参数随温度而变化。瞬态温度场下的材料参数每时每刻都在变化，这和恒定温度场下有所不同，在求解蠕变增量和应力增量的时候，需要考虑温度的影响。方程求解可以采用常刚度迭代法，所不同之处在于初应力和常刚度矩阵。具体实现过程如下：

弹性应力应变关系为

将弹性应力应变关系，应用到材料常数E和μ也随温度变化的情形，可以得到：

与不考虑温度影响的弹性增量应力－应变关系式相比，现在多增加了以初应力项出现的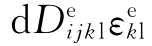，也即考虑了由于温度变化引起材料常数变化而产生的应力项。

将式（4－39）改写为如下的增量形式：

式中　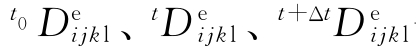——分别是其材料常数E、μ、G取t₀、t、t＋Δt时刻的弹性张量；

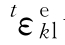　　　——t时刻的弹性应变；

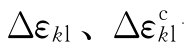　　　——分别是Δt时间增量内的总应变及蠕应变增量。

同理，根据增量形式的虚位移原理，即式（4－41），将Δu＝NΔa，Δε＝BΔa代入，可得到用初始弹性刚度矩阵表示的有限元方程，其矩阵形式如式（4－42）：

式中　t₀K_e——结构初始时刻的弹性刚度矩阵；

　　　ΔQ——不平衡力向量。

它们的表达式分别为

由于式（4－42）右端的Δε、Δε_c都是待求的未知量，同理需要迭代求解。迭代方程如下：

式中，Δε^（n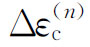）、是本增量步经过n次迭代以后的ε和ε_c的增量Δε、Δε_c；而左端的δa^（n＋1）是本增量步Δa的n＋1次修正量。Δε^（0）是本增量步开始迭代时的预测值，或者简单地取为零。

而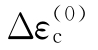的计算公式为

式中　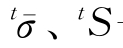——分别是t时刻的等效应力和偏应力；

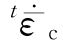　　　——等效蠕变应变率，由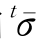和^t T决定。

在每次总体平衡迭代得到系统的位移增量Δa的修正量δa^（n）以后，进而利用几何关系可以得到δε^（n）以及Δε^（n＋1）＝Δε^（n）＋δε^（n）。在进行新的迭代之前，需要决定每一个高斯积分点的新的状态量，即由每一个高斯积分点的Δε^（n＋1）计算出该点的Δε^（n＋1）_c和Δσ^（n＋1）。而这三者构成以下的非线性方程组：

Δσ^（n＋1）＝D_e（Δε^（n＋1）－Δε_c^（n＋1））　　　　　　　　　　　　　　　（4－48）

上述非线性方程组的求解比较复杂，特别是由于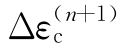强烈地依赖于应力状态σ，容易导致求解过程的不稳定。为此，可采用如下的迭代方案。

对于式（4－47）所表示的蠕变本构关系积分，为了保持数值稳定，宜采用隐式积分的广义中心法进行。在此情况下，以上非线性方程组可以改写成以下迭代求解形式：

式中

其中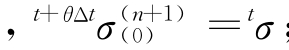；参数θ可在（0～1）之间选取，即满足0≤θ≤1。当θ≥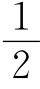时，算法是稳定的。式中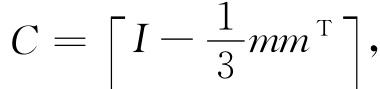m^T＝［1 1 1 0 0 0］。

求解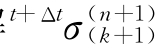的方程为

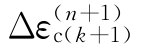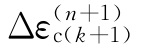当从该式解得以后，将其回代式（4－49），即可得到。将和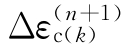进行比较，如果满足收敛准则：

则结束该积分点的迭代，并令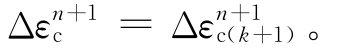

如果不满足收敛准则，则将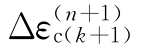代入，继续对该积分点进行下一次本构关系的迭代。当所有积分点的本构关系迭代完成以后，则将各个积分点的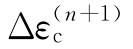和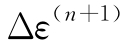代入式（4－45）的右端，并开始本增量步的系统平衡方程的下一次（n＋2）次的迭代。

值得注意的是，求取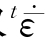应采用t时刻对应的材料参数，而求取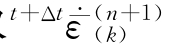应采用t＋Δt时刻对应的材料参数。

3）编程要点及框图

前面讨论了蠕变的有限元实现方法，从而为UMAT子程序编程提供了思路。ABAQUS提供了二次开发的平台，用户无需自编一套大型有限元程序，而只需编制UMAT子程序，借助接口参数与ABAQUS主程序进行数据的交换和调用。

UMAT子程序的编写采用Fortran语言，但需要注意的是，不同ABAQUS版本对应不同的编译环境，如ABAQUS 6.5版本，需要Compaq Visual Fortran 6.0和Microsoft Visual C＋＋Version 6.0支持进行编译；ABAQUS 6.6版本，需要Intel Visual Fortran 8.1和Microsoft Visual Studio.NET 2003支持才能进行正常的编译。

为了保证UMAT子程序的正常运行，用户在编写子程序时，必须遵循子程序编写规范，某些特定字符不得改变其原有特定定义，否则会产生意想不到的错误，也即用户能定义的参数仅仅是那些符合UMAT规定的“可被定义的参数”。

进行UMAT子程序编程时，需注意以下要点：

（1）ABAQUS中进行蠕变有限元分析时，一般采用两个分析步，首先是瞬态弹性分析步，然后是黏性分析步。因此，在编制UMAT子程序时，需区分瞬时弹性和蠕变，可用接口参数KSTEP作为判定依据。当KSTEP＝1，则为瞬时弹性分析；当KSTEP＞1，则为蠕变分析。

（2）在ABAQUS中，剪切应变采用工程剪切应变的定义，即γ_ij＝u_i，j＋u_j，i，所以剪切模量是G而不是2G。本UMAT子程序中采用的弹性雅可比矩阵DDSDDE形式如下：

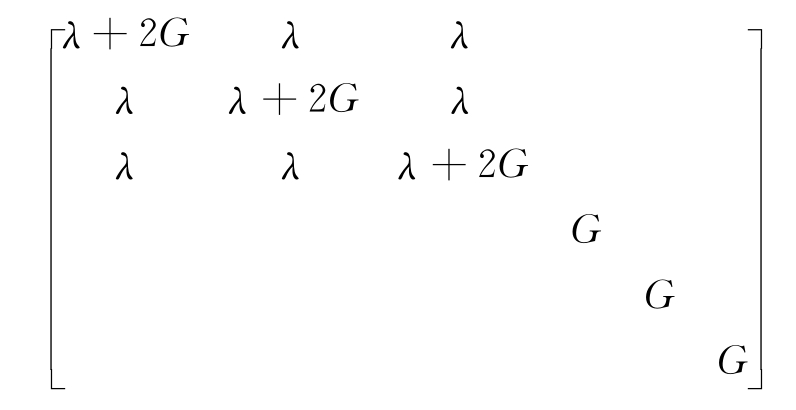
（3）在UMAT子程序的接口参数中，只有总应变STRAN，没有区分蠕变应变和弹性应变。因此，在编制UMAT子程序时，用户需定义蠕变应变和弹性应变作为状态变量保存在STATEV数组中。当然，用户还可以将需要的一些变量，如等效蠕变应变、等效黏弹性应变和等效黏性应变保存在STATEV数组中，以备输出到＊.odb文件中，进而在后处理模块中查看。

（4）状态变量STATEV数组需采用ABAQUS中的另外一个用户子程序SDVINI赋初值，对于本UMAT子程序，状态变量赋初值为0。

（5）对于某材料单元的一个积分点，一般来说，在每个增量步的每一次迭代过程中，需要调用UMAT子程序一次，但第一次迭代需额外多调用一次形成刚度矩阵。

（6）黏性分析时，ABAQUS主程序给定的总应变增量DSTRAN包含了弹性应变增量和蠕变应变增量，在求解蠕变应变增量和应力增量时，需进行多次迭代求解，因为蠕变增量强烈地依赖于应力状态，容易导致求解过程的不稳定。本次编程迭代求解非线性方程时，θ取为0.8。

（7）注意ABAQUS主程序更新应力、应变等变量的方式。对于每一增量步的每一次迭代，如果系统不平衡，则ABAQUS主程序会放弃本迭代步的应力、应变等变量的更新，回复到增量步初始时刻的变量值。只有当系统迭代平衡后，ABAQUS主程序才会更新应力、应变等变量。

（8）对总应变增量DSTRAN的理解。DSTRAN是一个总应变增量，真正的物理意义为某一增量步Δt时间内产生的总应变增量，而不是该增量步的每一次迭代步产生的总应变修正量，这一点对于UMAT子程序初学者来说，经常会产生误解。因为按照蠕变有限元的系统平衡方程，每次迭代得到一个试探应力σ（t_n＋Δt），进而进行系统平衡判断，如果不满足平衡判定标准，则得到总位移增量Δa的一个修正量δa^（n），根据几何方程可以得到总应变增量Δε的修正量δε^（n）＝Bδa^（n）。这时ABAQUS主程序并不把修正量δε^（n）传给UMAT子程序，而是先将总应变增量Δε进行更新Δε^（n＋1）＝Δε^（n）＋δε^（n），然后再传给UMAT子程序。

（9）瞬态温度场下的UMAT子程序需要根据当前积分点的温度值，在给定的材料参数之间自动插值对应温度下的材料参数。

瞬态温度场UMAT子程序的编程思路，如图4.13所示。

图4.13　瞬态温度场UMAT子程序编程思路框图

4）UMAT子程序源代码

按照上述编程思路框图，编制了瞬态温度场Burgers模型的UMAT用户子程序。由于源代码较长，为节省篇幅，本书略。源代码文件（burgers.doc和burgers.for）位于本书配套光盘＼Chapter 04＼01modified burgers model＼目录下。