相关理论和计算方法

8.1　相关理论和计算方法

1）周期性变温条件下的路面温度场边界形式

由于太阳辐射的作用，使得大气温度在昼夜之间产生明显的差异，并呈现出日周期性的变化特征。太阳辐射的这种周期性变化规律对路面结构温度场的影响可以近似地用周期性变化的边界条件描述。

在沥青路面结构（厚度、热学特性等）确定的情况下，影响其温度场的主要环境因素有日最高气温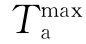、日最低气温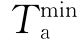、日太阳辐射总量Q、有效日照时间c以及日平均风速v_w。

（1）太阳辐射

根据Barber、严作人等的研究结果，太阳辐射q（t）的日变化过程可采用以下函数近似表示：

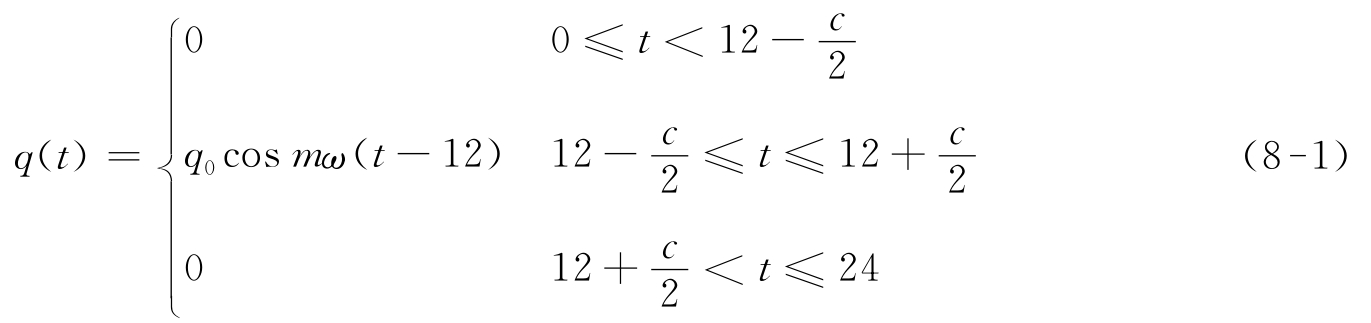
式中　q₀——中午最大辐射，q₀＝0.131m Q，m＝12/c；

　　　Q——日太阳辐射总量，J/m²；

　　　c——实际有效日照时数，h；

　　　w——角频率，w＝2π/24，rad。

上式为分段函数，不光滑连续，在计算温度场时会出现跳跃间断点，为此，需要将其展开为级数形式以得到光滑连续的函数表达式。根据Fourier级数的相关原理，可将上式展开为余弦三角函数形式的Fourier级数，即式（8－2），计算阶数k达到30即可满足工程精度的要求。

式中　a₀＝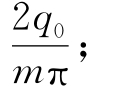

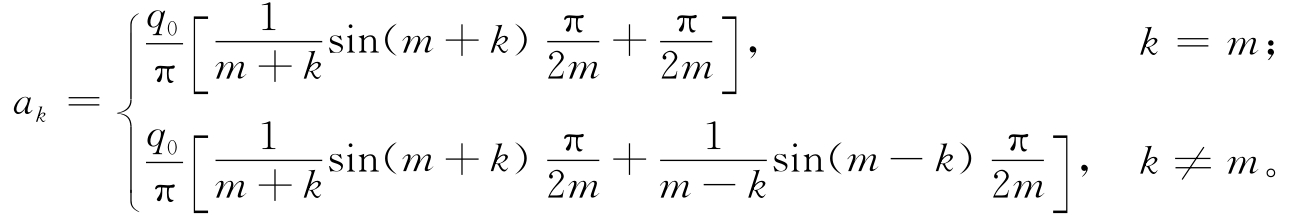
（2）气温及对流热交换

由于太阳辐射的影响，大气温度呈现出周期性的变化特征。由于日最低气温通常出现在黎明前后，大约在上午4～6时，而日最高气温大多出现在最大太阳辐射出现后约2h（下午14时左右），这样，从最低气温上升到最高气温不足10h，而从最高气温降至最低气温则需要14h以上，单一的正弦函数无法模拟这种实际的变温过程。为此，可采用两个正弦函数的线性组合式（8－3）来模拟气温的日变化过程，其结果与实际情况符合较好。

T_a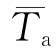＝＋T_m［0.96sinω（t－t₀）＋0.14sin 2ω（t－t₀）］　　　　　　　　　　　　　　　（8－3）

式中　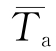——日平均气温，℃，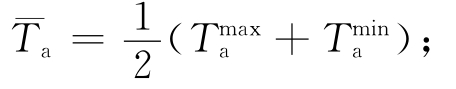

　　　T_m——日气温变化幅度，℃，T_m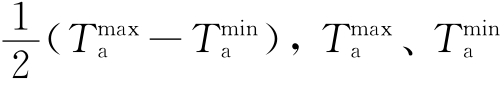＝分别为日最高与最低气温，℃；

　　　t₀——初相位，最大太阳辐射与最高气温的出现时间差加7，一般情况下，设时间差为2h，为此，可以取t₀＝9；计算时，t以小时计。

路面表面与大气产生热交换的热交换系数h_c主要受风速v_w的影响，两者之间呈线性关系：

h_c＝3.7v_w＋9.4　　　　　　　　　　　　　　　（8－4）

式中　h_c——热交换系数，W/（m²·℃）；

　　　v_w——日平均风速，m/s。

（3）路面有效辐射

路面有效辐射的大小主要与地面温度、气温、云量、空气的湿度及透明度等诸多因素相关。以往的研究大多通过适当改变路表面放热系数以修正气温，或者对太阳辐射的幅值进行折减等方法来近似计算路表面有效辐射的释热效果。但这种处理方法存在较大误差，可采用下式直接实现地面有效辐射的边界条件：

q_F＝εσ［（T₁ |_Z＝0－T_Z）⁴－（T_a－T_Z）⁴］　　　　　　　　　　　　　　　（8－5）

式中　q_F——地面有效辐射，W/（m²·℃）；

　　　ε——路面发射率（黑度），沥青路面取0.81；

　　　σ——Stefan－Boltzmann常数（黑体辐射系数），σ＝5.669 7×10^－8 W/（m²·K⁴）；

　　　T₁| _Z＝0——路表温度，℃；

　　　T_a——大气温度，℃；

　　　T_Z——绝对零度值，℃，T_Z＝－273℃。

提示：对于“气温及对流热交换”和“路面有效辐射”，在ABAQUS/CAE的Interaction模块中进行定义，对于“太阳辐射”在Step模块中进行定义。

2）沥青路面结构车辙的计算

（1）ABAQUS中的蠕变模型

ABAQUS对于各向同性材料的蠕变特性常用的描述方式有两种：时间硬化蠕变模型和应变硬化蠕变模型。一般采用ABAQUS中时间硬化的蠕变模型进行车辙计算分析。

提示：也可以采用本书第4章中的修正Burgers模型进行沥青路面车辙计算。

路面材料的蠕变变形ε_cr可以表示为温度T、应力q和时间t的函数，即

ε_cr＝f（T，q，t）　　　　　　　　　　　　　　　（8－6）

来分析蠕变变形，通常采用Bailey－Norton蠕变规律。若所受应力保持不变时，时间硬化蠕变模型的表达式为

ε_cr＝C₁q^C₂t ^C₃　　　　　　　　　　　　　　　（8－7）

式中　q、t——分别表示应力和时间；

　　　C₁、C₂和C₃——依赖于温度的模型参数，可以通过材料试验确定，通常C₂≥0，C₃≤1。

上式中，假定q不随时间t变化，有

令

则有

上式即为ABAQUS中的时间硬化蠕变模型（以蠕变率表示），A、n、m为模型参数。通常，A，n＞0；－1＜m≤0。

（2）连续变温的沥青路面车辙模拟分析方法

在环境因素的影响下，实际路面结构的温度随路面深度和时间时刻在发生着变化，其温度场为瞬态温度场。而作为路面材料的沥青混合料，其黏弹性性质很显著，材料特性受温度影响很大，尤其是高温情况下，影响则更为显著。故在路面车辙分析时，应引入路面结构的实际温度场，考虑材料特性随温度的连续变化，建立连续变温（随空间和时间）的车辙模拟分析方法，以分析路面车辙的变化规律。

此外，由于研究中所采用材料模型分别为蠕变模型和弹性模型，即在计算出的总变形中包括蠕变变形和弹性变形两部分，而车辙（永久变形）主要由蠕变变形产生，弹性变形在载荷卸载后自动恢复，不属于永久变形，因此，在计算车辙量时应将总变形减去模型的弹性变形部分。

瞬态连续变温的沥青路面车辙模拟分析方法的原理及步骤如图8.1所示。

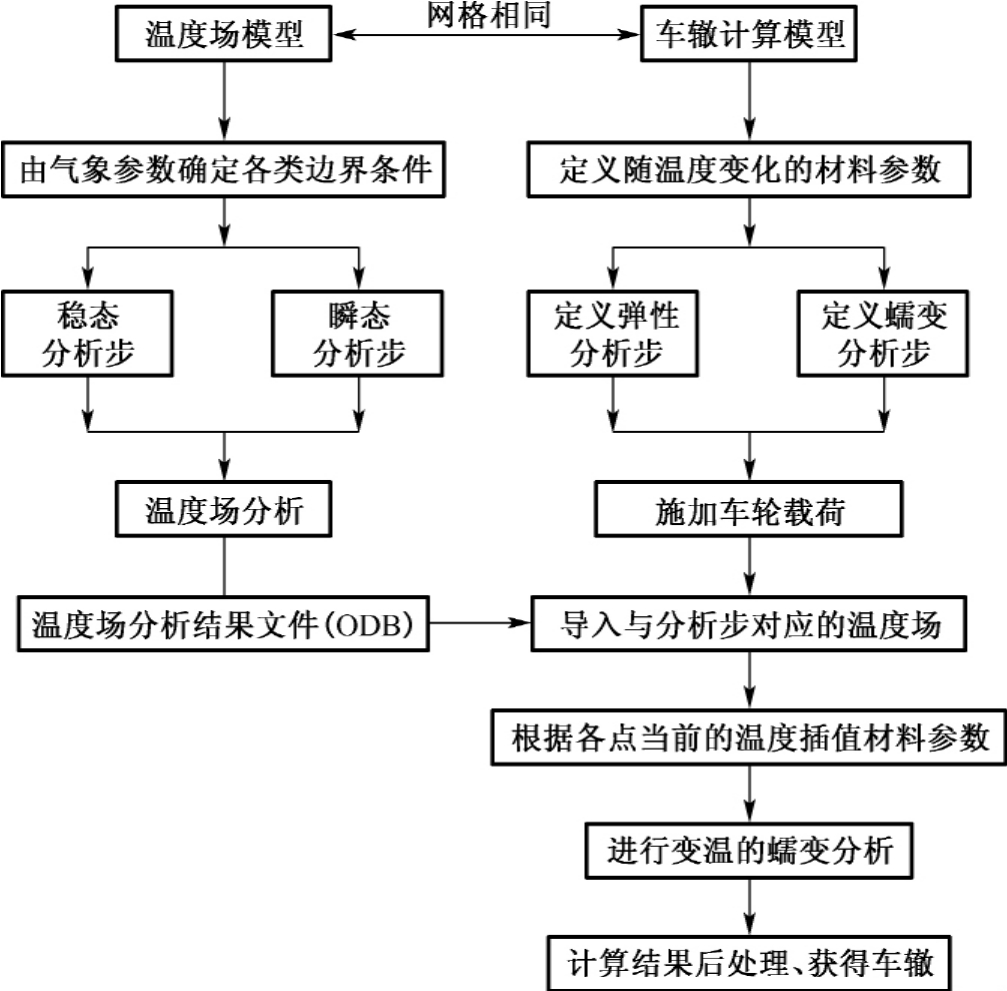
图8.1　连续变温的沥青路面车辙模拟分析方法原理及步骤

上述瞬态连续变温的沥青路面车辙模拟分析方法，在ABAQUS软件有限元分析中的具体实现方法如下：

①根据适当的温度边界条件建立温度场计算模型，进行路面结构的温度场数值分析；

②根据以下步骤建立车辙计算整体模型，进行变温条件下的车辙模拟计算：

（a）采用与温度场分析相同的车辙计算模型；

（b）在Property模块中，定义随温度变化的材料参数；

（c）在Step模块中，建立弹性分析步（Static），分析步时间设为足够小量（建议取1×10^－10）；

（d）在Step模块中，建立蠕变分析步（Visco），分析步总时间设为载荷累积作用时间；

（e）在Load模块中，施加静态车轮载荷；定义与各蠕变分析步相对应的路面结构温度场变量（将①分析出的相应时间温度场导入车辙分析模型中，用＊.rpt文件或者＊.odb文件均可，建议采用统一的＊.odb文件）；

（f）在每一步分析前，程序根据每一结点当前的温度值自动插值材料参数，代入分析模型，进行蠕变数值计算分析。

③在后处理分析中，将各点蠕变分析步中的总变形减去弹性分析步的弹性变形，得到永久变形，即为车辙量。

此外，由于蠕变分析为非线性分析，需要大量迭代，同时又考虑材料参数随温度的变化，其插值计算时间较长，输出变量所用空间也很大。因此，在分析步中，只需在Step模块中定义与蠕变有关的面层材料各结点的位移、蠕变和应力作为输出要求，尽量减少运算时间和所需空间。