上限法与满意度的并合算法

（二）算法分析

1.可能度与满意度曲线的数学形式

上面已对可能－满意度方法的基本思路作了说明，对一个事件的可能度和满意度含义有了明确的定义，但在实际应用中，要用什么样的数学方法来描述可能度和满意度呢？根据可能度和满意度的定义，我们可用三折线、S型曲线等曲线的数学形式来表示可能度和满意度，如对可能度P的描述，我们用三折线表示如下式（7）：

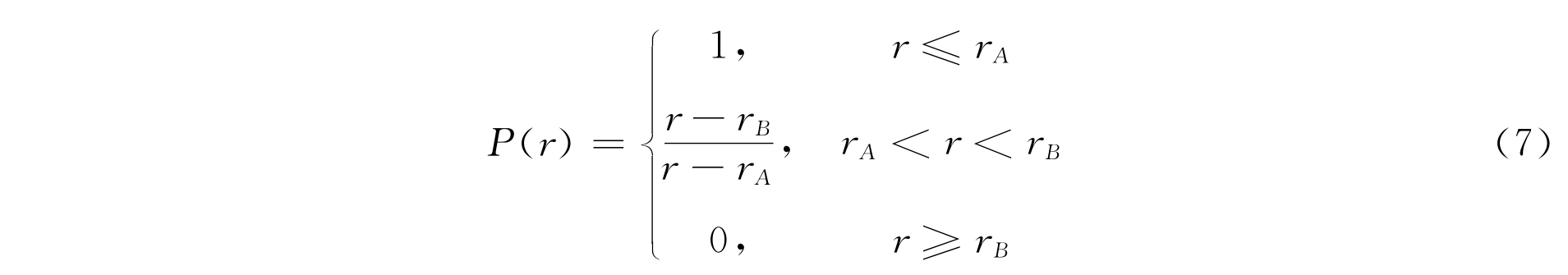
用图4.1表示如下：

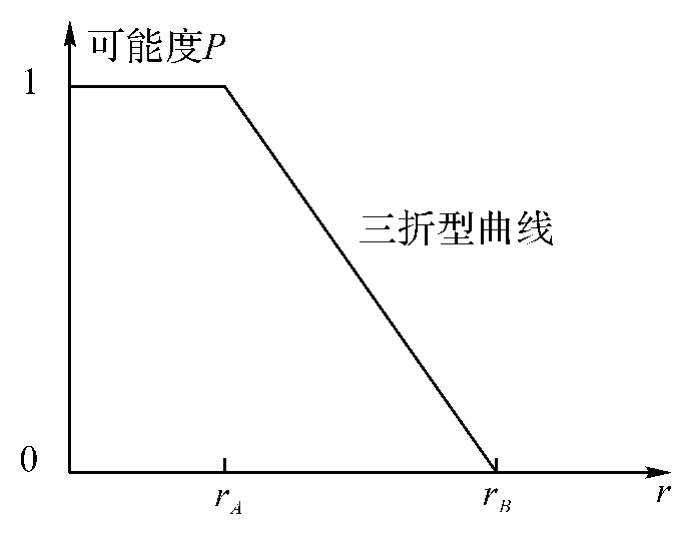
图4.1　可能度的三折型曲线

这是一种“抓两头，插中间”的粗略办法，这种方法关键在于定出A、B两个转折点。确定A、B点的途径很多：一是凭借较为长期的实践经验；二是对产品用户进行调查统计；三是根据厂方提出的数据；四是自行试验统计；五是进行分解研究；还有向专家、行家们请教的。资料掌握得愈详尽准确，讨论得愈全面深入，各方面的观点又较一致，则A、B点的横坐标可定得愈准确。在p（或q）＝1或p（或q）＝0时，常争论较少；在p（或q）＝（0，1）的区间上，可能有较多争论，反映了把握不大的现状。这种可粗略可精细的方法给类似于人口与能源等复杂问题的讨论带来了较大的方便。

除了三折型曲线，还有S型曲线，这也是比较常用的一种曲线。我们在对深圳人口容量研究时，主要采用了此类曲线。用数学形式表示如下：

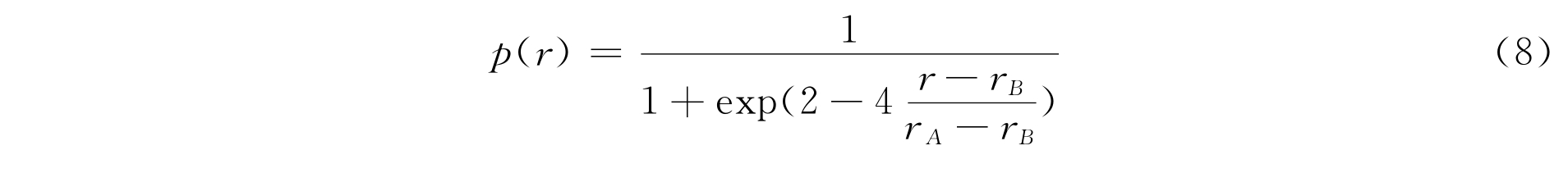
用图4.2描述如下：

如果对某一个具体的问题，如果已经研究得很透彻而能具体做出其更为确切的可能度曲线，则不必拘泥于此类方法。

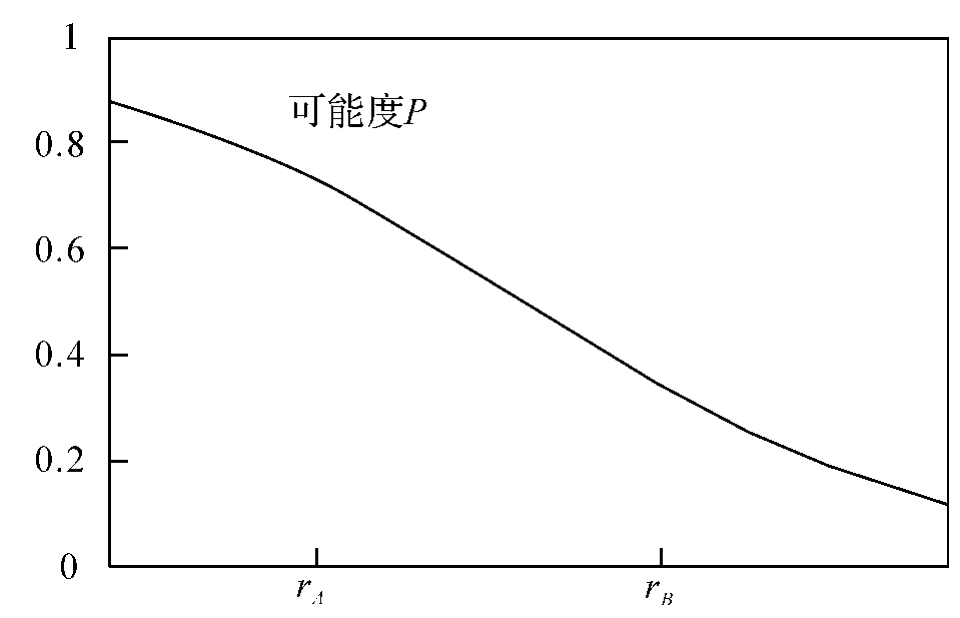
图4.2　可能度的S型曲线

满意度曲线q（s）的数学形式类似于上述的可能度曲线形式，在此不再赘述。

2.可能度与满意度的并合算法

如上所述，可能度与满意度可以并合为可能－满意度曲线，它分强并合和弱并合两种方法。

如果有p（r）、q（s）及f（r，s，α）等的函数式，则可能－满意度可以获得相应的公式解。

（1）当限制条件为r＝αs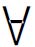，r，s∈R¹（实数集），则可得p（r）和q（s）为三折型曲线时的弱并合解为：

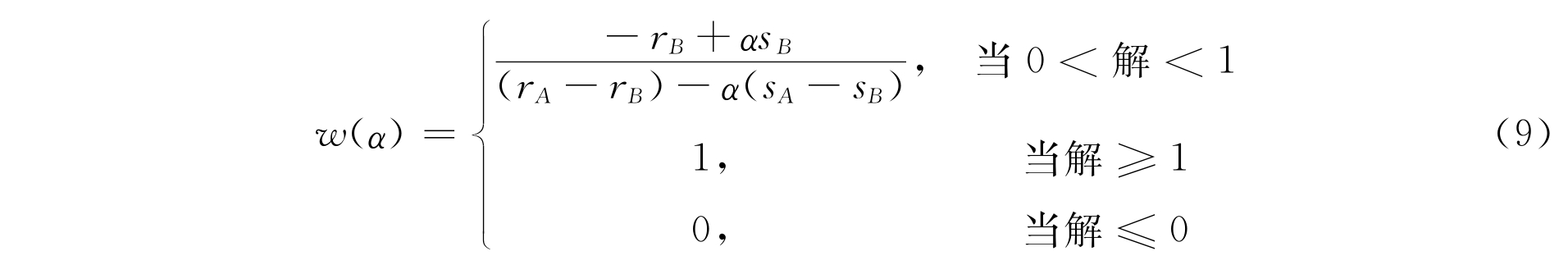
当p（r）和q（s）为式（8）的S型曲线时的弱并合解为：

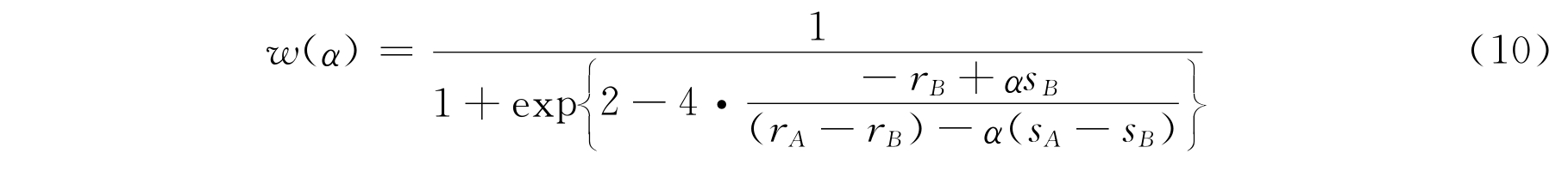
（2）当限制条件为α＝rs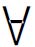，r，s，α∈R¹，则可得三折型弱并合解为：

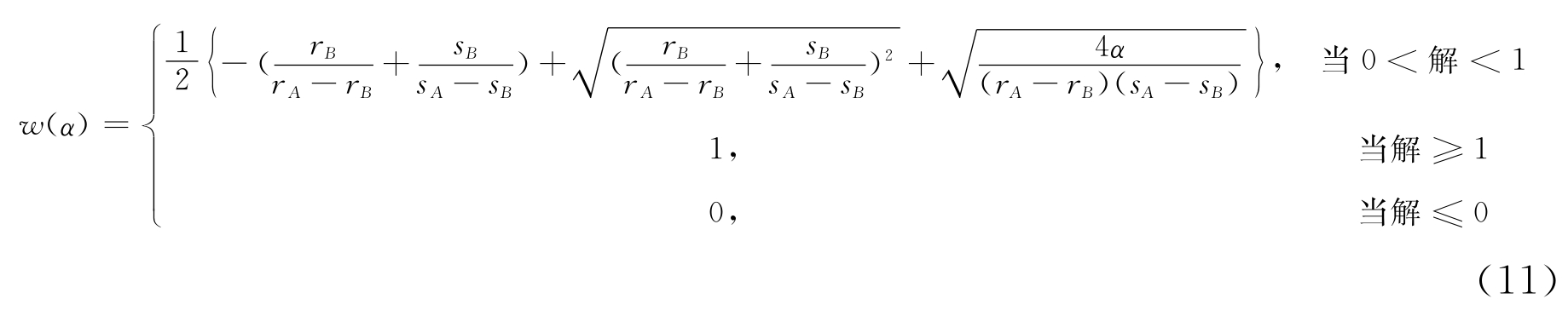
（3）当限制条件为α＝r＋s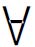，r，s，α∈R¹，则可得三折型弱并合解为：

这些不同的并合算法在不同的规划问题中得到相应的应用，如涉及总产量、人均产量等因素推求人口的问题，都具有r＝αs的限制条件类型；而在耕地面积、每亩单产推求产量时就属于第二种算法。

3.两条以上可能－满意曲线的并合方式

在计算出若干条可能－满意度曲线后，在做决策分析时，要对多条曲线进行并合分析，在并合的算法上，有多种并合的方式，在此主要考虑三种可能－满意度曲线间的并合算法。

设有两条可能－满意度曲线w1、w2，它的以下几种并合算法表示如下：

弱并合：符号为＜…（Mm）…＞，特例为＜…（m）…＞。

强并合：符号为＜…（M·）…＞或＜…（·）…＞。

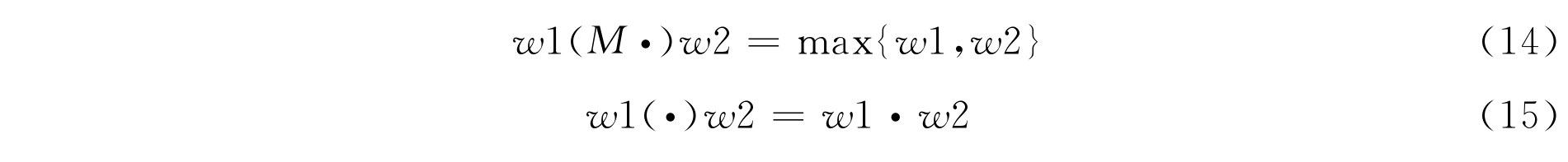
变权加和：符号为＜…（M＋）…＞。

4.P－S可能－满意度多目标决策方法的优点

P－S法最大的特色就是提供了一种可以综合考虑多因素制约时决策的工具。传统人口规划的因素分析，其结果的现实有效性往往需要引用“短边原理”（或称“木桶原理”，指该条件必须满足但又最难满足，如同最低门槛，其意义相似于P－S法中的弱并合）来证明约束条件是瓶颈因素，而这一办法常用来估算人口容量的上限而非最优解。当面对人们不同适应性和选择性的时候，单因素分析给出的上限值的实际意义有限。但P－S法由于其概念、方法与模糊理论的关系，在面对这一复杂的系统问题时往往能够做到游刃有余。

在运用P－S法作适度人口规划时，对纳入模型的约束因素需要审慎考虑。纳入因素过多，会增加模型的复杂性，增加计算量和为参数赋值收集资料的难度，而过多约束因素如果有的不重要或与分析对象没有必然的约束关系，反而会冲淡主要约束因素的作用。当然，约束条件过少不能全面反映问题，也会失去运用P－S的本意。因此，抓住主要矛盾，选取主要的、根本性的约束因素纳入模型，便成为决定建模成功与否的重要环节。合适的选择约束因素不仅能减少运算量，而且能有效减少给过多因素的参数赋值过程中所带来的主观上的偏差。因此，在构成模型时必须仔细考虑，取消不必要的约束条件。

P－S法赋值较宽松，并且随可能－满意度的调整和合并方法的不同而给定不同的适度人口规模，有一定的灵活性，因此在短期预测中意义不大，但是该方法能够反应主要的、带根本性约束的综合作用，适合用于我们所研究的深圳市的人口容量和适度人口的课题研究当中，它能对研究对象的中长期目标规划做一定的决策作用。

该方法已有许多学者用于适度人口的研究，如上海交通大学王浣尘教授领导的《上海人口合理规模研究报告》课题组，利用该方法对上海市的人口容量做了细致的研究，他们从制约和影响人口规模的各种有关因素出发，采用多目标决策技术和分解综合的办法，在充分考虑各种社会经济因素对人的生活影响的前提下，通过做出这些不同的因素制约下的可能－满意度曲线，将之放在同一个以人口为横轴、可能－满意度为纵轴的坐标系下，直观地观察受控于不同因素下描述可能－满意度与人口互动关系的曲线，并据此方便地找出限制可能－满意度提高的“瓶颈”因素。该方法引进了可能－满意度指标时选定影响上海合理人口规模25项因素，在几种不同的假设下，计算多种方案的可能－满意度数值，提出50年后上海市的合理人口规模。