观察场模型

观察场的主要作用是拟合原始的观察数据，通过拟合的数据反映每一个像素位置的特征信息，目的是使图像分割的结果能保留更多的细节信息。观察场建模的方法比较常用的是高斯混合模型（FGMM模型）和高斯马尔可夫模型（GMRF模型）。

2．3．4．1 FGMM模型

1．FGMM模型特征建模

FGMM模型假设图像每个区域的观察值可以通过高斯函数来表示，整幅图像的观察特征可以视为这些高斯函数的混合，即图像的观察数据的概率分布可以视为几个高斯函数的加权和来表示，其图像观察数据的概率分布为：

其中，ys表示观察位置s处的观察值；m＝1，2，…，k表示观察位置的隐状态；f（ys｜xs＝m）为对应类别的高斯概率密度函数，即：

2．FGMM模型的参数估计

根据每个像素的位置标记将像素分为K类，直接计算每个类别的参数：

其中，Nm是图像中被标记为第m类的像素的个数；N是整幅图像的像素的个数。

由于标号场X是一个隐随机场，因此观察到的图像数据是一个不完全的数据集合；对不完全的数据集合的参数估计，可以采用EM算法进行估计。给定观察数据y，混合模型的不完全数据的似然函数为：

由于在对数运算中包含了求和项，因此很难获得最大值。利用EM算法可以进行计算。

算法的E步骤表示为：

其中，t表示迭代次数表示第t次迭代的参数。算法的M步骤表示为：

式中，N表示图像像素的个数。EM算法在步骤E和步骤M之间不停地迭代计算，这个过程中参数估计和图像分割交替进行，直到算法收敛结束。

2．3．4．2 GMRF模型

1．GMRF模型的观察场建模

假设多光谱纹理图像表示为：y＝｛y1，y2，…，y N｝，每个像素位置的像素取值表示为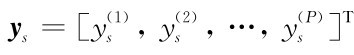：，给定区域A内的GMRF模型的条件概率密度函数表示为：

其中，为零均值的高斯噪声向量。在多光谱图像中，像素的空间相关性表示为：

其中为区域A内所有像素的均值向量；ηs表示位置s处的邻域距离s的偏移量的集合；θji为GMRF模型中第j帧与第i帧的邻域交互系数，如图2．8所示。

图2．8 GMRF模型空间交互参数示意图

∑表示条件协方差矩阵，用来描述帧间两两相互关系的数字特征，公式如下：

其中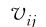，ij是（i）e（j）的数学期望。

2．GMRF模型的参数估计

（1）GMRF的最小二乘法参数估计。对于给定的区域A，采用GMRF模型建模区域内所有像素所组成的观察场，则参数θ通过最大化获得：

其中，P（xs｜xs＋r，r∈ηs）为GMRF模型的概率密度函数。。参数的最小二乘估计参数为：

其中，qs＝col［xs＋r－xs－r］；NA为区域A中像元的个数。

（2）GMRF的极大伪似然参数估计

对于一个给定区域A，采用GMRF模型建模区域内所有像素所组成的观察场，则区域A的似然函数表示为：

式（2－33）表示图像区域A中所有像素的条件概率密度的乘积。由于图像各个像素之间并不是相互独立的，因此该函数表示的并不是真正意义上的似然函数，通常称之为伪似然函数。对于伪似然函数L（θ）对每一个GMRF参数求导，可得到一系列线性方程。通过解线性方程组，可以得到θ的极大似然估计值。下面以第j帧中的像素s为例，其参数θj的求解过程如下：

其中。如果令 ，则式2．34可以简写为：

由于噪声（j）s 的自相关函数是对称的，各个邻域系列以及其相关的系数也是对称的，即rηs－r∈ηs＋r，而且，因此，所有邻域的相关系数可以通过同步求解获得。设η－s是非对称的半平面邻域系列，与ηs之间的关系为：

同步求解方程表示为：

其中，

则条件协方差矩阵表示为：

其中，NA为区域A中像元的个数。