概念教学中应重视培养学生的转化思想

概念教学中应重视培养学生的转化思想_青年学术论坛

概念教学中应重视培养学生的转化思想

湖北省体育运动学校　杨　军

课堂教学是实施素质教育的主渠道，如何优化数学教学过程，提高教学效益，是目前素质教育中一项重要的研究课题。新的数学教学大纲把数学思想方法纳入基础知识的范畴，是加强数学培养的举措，也是现代信息社会的要求。数学教学的目的是让学生通过数学知识的学习，了解和掌握基本的数学思想和方法。数学思想方法的教学，是把传统的知识型教学转化为能力型教学的关键，是培养有创造性人才的良好手段和渠道。

任何数学问题解决的过程，实际上是实现条件向结论，未知向已知的转化过程。因此，转化是数学最基本的思想。它要求在处理问题时，用联系、发展运动变化的眼光观察事物，分析问题，有意识地对问题进行转化，使其变为已经解决过或易于解决的问题，进而使问题顺利获解。转化思想渗透在中学数学的各个环节之中。

数学概念教学是数学教学的重要组成部分。在教学过程中结合数学概念，渗透转化的思想，不仅有利于加深对概念的理解，而且对于开发学生智力，培养学生能力，发展学生思维，具有十分重要的意义。

一、在概念教学中培养学生的转化思想的必要性

（1）中学的数学教学愈来愈重视对学生“用数学”的意识和能力的培养。所以，熟悉教学转化的思想，有意识地运用数学变换的方法去灵活解决有关数学问题，将有利于强化在解决数学问题中的应变能力。有利于提高解决问题的思维能力和技巧。

（2）概念、定理、公式等知识是数学的外在表现形式，这些知识的记忆是短暂的，而蕴含于知识中的方法和思想的掌握则是长远的，对学生的思维及整体文化素质，将产生深刻而持久的影响，使他们受益终生。

（3）正确理解数学概念是掌握数学基础知识的前提，只有概念明确，才能判断恰当，推理有据，方法得体，思维流畅，在概念教学中，如果只是简单地给出定义，进行灌输和记忆，不注意概念的转化功能，将导致学生听得懂课，就是不会解题，长此下去，会使学生思维僵化，阴碍学生创造力的发展和培养。因此，在教学中培养转化意识，不仅有利于用活概念，而且有助于更深刻地理解数学概念。

二、在概念教学中培养学生转化思想的方法

1．通过概念的形成揭示转化的过程　在数学概念的形成过程中，要激励学生亲自尝试，主动建构。使学生在参与教学活动中了解转化的原因、依据、方法，从而在以后的运用中变成一个有意识的行为。例如：立体几何中“异面直线所成角”的概念，我们从研究异面直线的相对位置的需要出发，揭示异面直线所成角出现的背景，明确研究的必要性，通过联想平面几何中如何用数学量刻画平行直线和相交直线间的相对位置，逐步迁移到新问题的解决，利用转化将异面直线所成的角转化为相交直线所成的角，从而概括出定义。

在教学过程中，我们让学生通过类比、联想及直观的方法逐渐引出概念，了解转化的过程，理解定义的合理性。如果不对教材进行处理，学生听课将只知其然，而不知其所以然。

2．通过联想，顺用定义转化　定义是分析，解决问题的重要依据，巧妙简捷的解题常常来源于对定义的恰当合理应用。只有熟练掌握每个定义的本质属性，才能灵活地应用定义进行解题。

【例1】　已知f（x）＝x⁵＋a x³＋bx－8，且f（－2）＝10的值，试求f（2）的值。

分析：显然，由已知条件无法确定字母a、b的值，直接求出f（2）的值不易。引导学生观察这里自变量的关系－2与－2互为相反数，联想自变量互为相反数时函数值的关系在函数奇偶性中讨论过。由此想到利用函数的奇偶性的定义求解。这里注意到g（x）＝x⁵＋a x³＋bx是奇函数。

解题后的反思：在解题过程中，如果我们找不到合适的定理或方法，那么回到定义也许会是明智之举。

3．转换思维角度，逆用定义　对于有些数学问题，如果从正面直接探求，常常一筹莫展。但是，若改变一下思维的角度，避免正面强攻。从问题的反面进行逆向思考，又常能找到解题的通道。中学生在解题过程中往往习惯于正向使用，而对定义的逆用缺乏自觉性和敏感性。通过逆用定义解题，对于培养学生的逆向思维能力是大有好处的。

【例2】　过平面外一点与平面内一点的直线与平面内不经过这点的直线是异面直线。

分析：证明异面直线除了定义外别无他法，但要正面说明两条直线不同在任何一个平面内是非常困难的，因此我们考虑用定义的反面。

【例3】　设f（x）是定义在区间（－1，1）上的奇函数，且f（x）在（－1，1）上单调递减，求使f（1＋a）－f（1－a²）＜0成立的a的取值范围。

分析：这里不知道f（x）的解析式，因此f（1＋a）及f（1－a²）的表达式也不能得出。考虑到减函数的概念，若f（x）为给定区间上的减函数，则对该区间上任意的x¹＜x²，都有f（x¹）＞f（x²）反过来，若f（x¹）＞f（x²），则x¹＜x²，从而将函数值大小的比较转化成比较自变量的大小，这样同时可加深减函数概念的理解。

4．通过变式深化对概念的理解

（1）变通一下思路，当从某个角度难以入手或思路受阻时，换一个角度试试常常会给解题者带来希望。

（2）变通一下说法，为利用定义创造条件。每当我们碰到一个问题，感到提法有些生疏，概念有些模糊时，最好先用一些熟悉的语言，重新叙述一下。这看起来似乎只是语言上的说法不同，实质上是自身对问题认识和理解程度的深化过程。变换说法之后，一些神秘莫测、无从下手的问题会变得比较清楚、容易。

【例5】　已知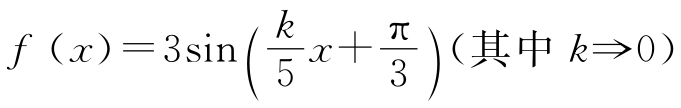，设对任意的－3≤C≤3。在任意相邻两个整数之间存在这样的x，使f（x）＝C成立，求满足此条件的最小正整数k。

分析：本题的语言抽象难懂。如能换个说法：“f（x）对任意－3≤C≤3，在任意相邻两个整数之间存在这样的x，使f（x）－C＃，也就是说：在任意相邻两个整数f（x）出现一个周期，亦即f（x）的最小正周期不大于1。这样问题就迎刃而解。

（3）变换一下位置。

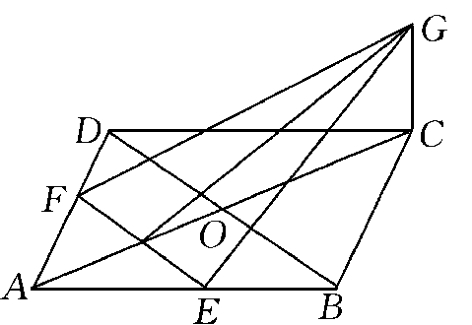
【例6】　已知ABCD是边长为4的正方形，E、F分别是AB、AD的中点，GC垂直于ABCD所在平面，且GC＝2，求点B到平面EFG的距离。

分析：这里要求点B到平面EFG的距离，根据点到平面距离的定义，必须确定B点在平面EFG上的垂足位置。但寻找B点在平面EFG上垂足位置比较困难。由于直线与平面距离的定义可将所求距离转化为求直线BD到平面EFG的距离，进而转化为求正方形中心O到直线GH的距离。另外，还可将点B到平面EFG的距离转化为求三棱维B－EFG底面EFG上的高的问题。

（4）利用概念的多种表述形式进行转化，培养学生思维的广阔性。有些概念有多种不同的等价形式，教学中引导学生从不同方面，不同角度去思考、去分析、去探索，有利于优化学生思维的广阔性。例如：复数的概念是围绕它的三种表示形式展开的。在运用中要注意选择适当的复数表示形式，正确进行各种形式间的相互转换。