不定积分与定积分

1.3.1　不定积分与定积分

1.不定积分、定积分的概念与性质

(1)不定积分的概念与性质

若在区间I内，F'(x)=f(x)，则称函数F(x)为函数f(x)在区间I内的原函数，而函数f(x)的带有任意常数项的原函数F(x)+C称为函数f(x)在区间I内的不定积分，记作∫f(x)dx，即

∫f(x)dx=F(x)+C.

不定积分具有如下性质:

①∫［f(x)±g(x)］dx=∫f(x)dx±∫g(x)dx.

②∫kf(x)dx=k∫f(x)dx(k是非零常数).

(2)定积分的概念与性质

设函数f(x)在［a，b］上有界，将［a，b］任意划分成n个小区间

［x₀，x₁］，［x₁，x₂］，…，［x_n－1，x_n］(x₀=a，x_n=b)，

任取ξ_i∈［x_i－1，x_i］(i=1，…，n)，记λ=max{Δx₁，…，Δx_n}.若极限

总存在(即极限不依赖于对［a，b］的分法与ξ_i的取法)，则称函数f(x)在［a，b］上可积，并称上

述极限为f(x)在［a，b］上的定积分，记作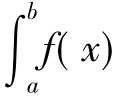dx，即

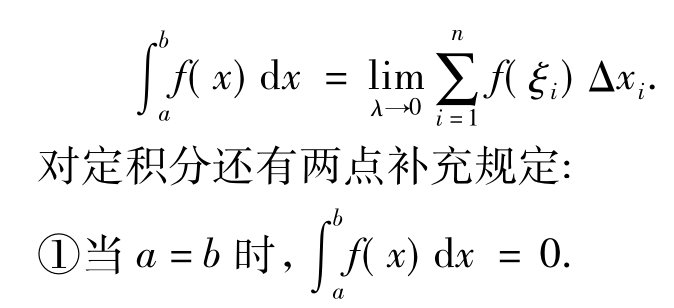
②当a＞b时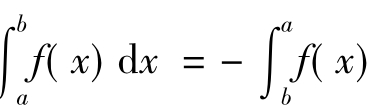，dx.

在［a，b］上f(x)≥0时，定积分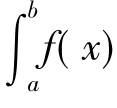dx在几何上表示由曲线y=f(x)、两条直线x=a，x=b与x轴所围成的曲边梯形的面积.

定积分具有如下性质:

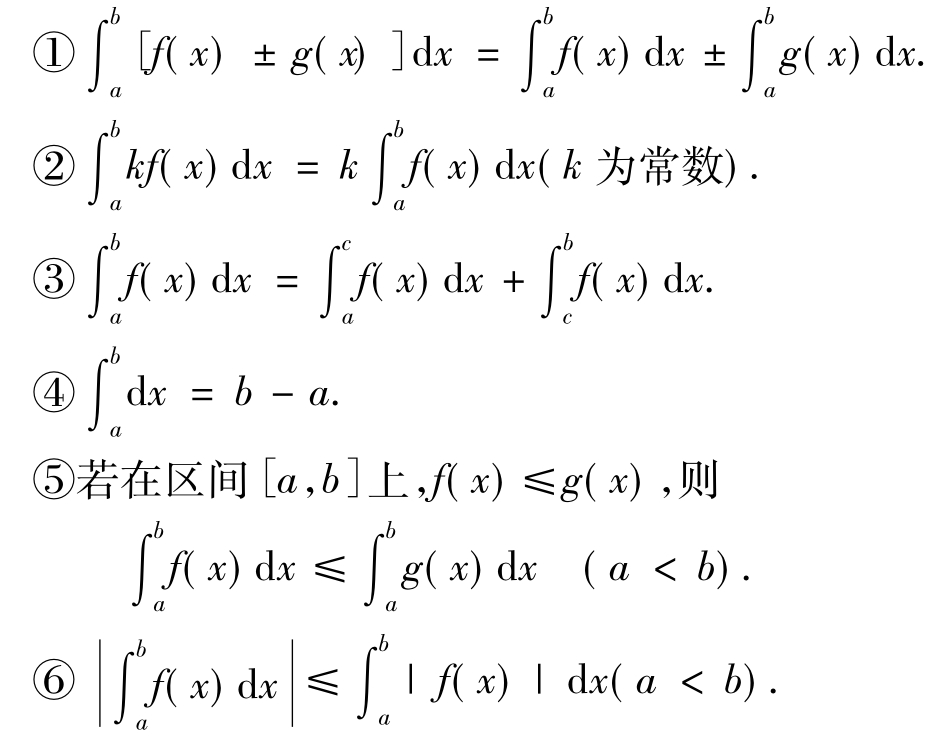
⑦设M，m分别是f(x)在［a，b］上的最大、最小值，则m(b－a)≤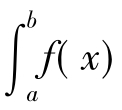dx≤M(b－a)(a＜b).

⑧(定积分中值定理)设f(x)在闭区间［a，b］上连续，则存在ξ∈［a，b］使得

2.微积分基本公式(牛顿—莱布尼茨公式)

设f(x)在［a，b］上连续，x∈［a，b］，则称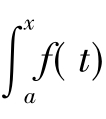dt为上限函数.

记F(x)=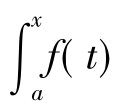dt，x∈［a，b］，则F'(x)=f(x)，即F(x)是f(x)的一个原函数.这表明连续函数f(x)的原函数一定存在，且可表示为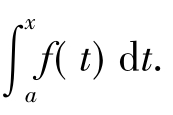

一般地，有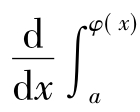f(t)dt=f［φ(x)］φ'(x).

由以上结果，可得微积分基本公式:

若在［a，b］上有F'(x)=f(x)，则

这个公式揭示了定积分与被积函数的原函数或不定积分之间的联系，给定积分提供了一个有效而简便的计算方法.

3.积分法

1)基本积分表

①∫kdx=kx+C(k是常数).

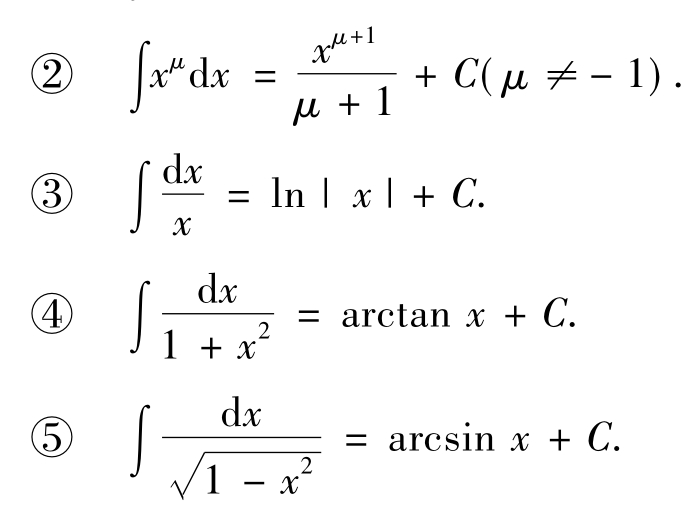
⑥∫cosxdx=sinx+C.

⑦∫sinxdx=－cosx+C.

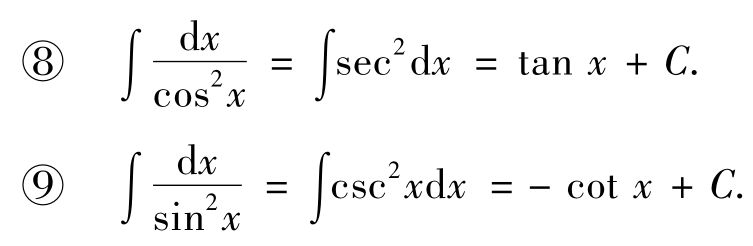
⑩∫secxtanxdx=secx+C.

∫cscxcotxdx=－cscx+C.

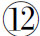∫e^xdx=e^x+C.

∫shxdx=chx+C.

∫chxdx=shx+C.

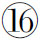∫tanxdx=－ln|cosx|+C.

∫cotxdx=ln|sinx|+C.

2)换元积分法

对不定积分，有第一类换元法和第二类换元法.

(1)第一类换元法

设函数f(u)有原函数，u=φ(x)可导，则有

第一类换元法也叫凑微分法，能否熟练地凑微分，是求不定积分的重要技巧之一.下面列出了一些常见的凑微分的形式:

(2)第二类换元法

设x=ψ(t)是单调的可导函数，且ψ'(t)≠0，又设f［ψ(t)］ψ'(t)有原函数，则有

其中t=ψ^－1(x)是x=ψ(t)的反函数.

第二类换元法，常用的代换有:三角代换、倒代换.如果被积函数含有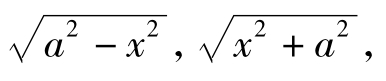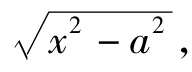可以依次作代换x=asint，x=atant，x=asect用来化去根式，即

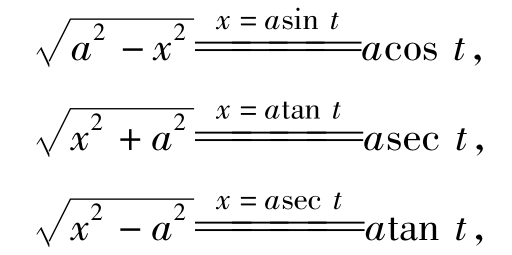
以上各式中，均假设a＞0.

倒代换主要用于消去被积函数的分母中的变量因子x.

(3)定积分换元法

对定积分，有定积分换元法.

假设函数f(x)在区间［a，b］上连续，函数x=φ(t)满足条件:

①φ(α)=a，ψ(β)=b;

②φ(t)在［α，β］(或［β，α］)上具有连续导数，且其值域R_φ＞［a，b］，则有

对定积分的换元法有两点值得注意:

①用x=φ(t)把原来变量x代换成新变量t时，积分限也要换成相应于新变量t的积分限;

②求出f［φ(t)］φ'(t)的一个原函数Φ(t)后，不必像计算不定积分那样，再要把Φ(t)变换成原来变量x的函数，而只要把新变量t的上、下限分别代入Φ(t)中，然后相减就行了.

利用定积分的换元法，可得有关奇、偶函数在关于原点对称的区间上的积分的下述性质.

性质1若f(x)在［－a，a］上连续且为偶函数，则

性质2若f(x)在［－a，a］上连续且为奇函数，则

利用定积分的换元法，可得下面的重要公式

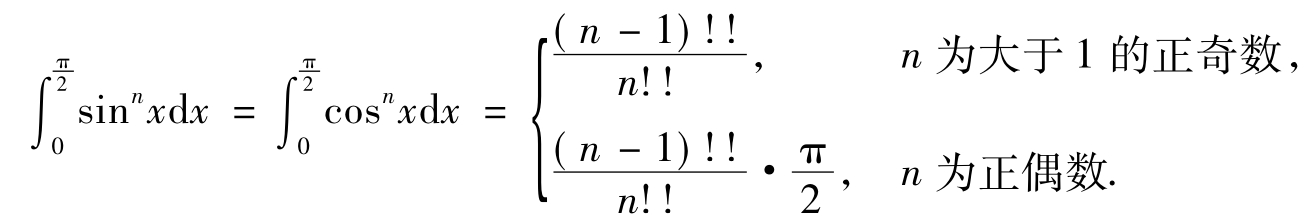
3)分部积分法

对不定积分，有

∫u(x)dv(x)=u(x)v(x)－∫v(x)du(x).

对定积分，有

如果求积分∫u(x)v'(x)dx有困难，而求积分∫u'(x)v(x)dx比较容易，那么利用分部积分公式，就能起到使积分化难为易的作用.

应用分部积分时，恰当选取u(x)和dv(x)是一个关键.选取u(x)和dv(x)一般要考虑下面两点:

①v(x)要容易求得;

②∫v(x)du(x)要比∫u(x)dv(x)容易积出.

分部积分法主要用于被积函数是两个不同类型的函数乘积的积分，特别在下列三种情形下一般采用分部积分.

①被积函数是幂函数和对数函数或幂函数和反三角函数的乘积，就可考虑用分部积分法，并设对数函数或反三角函数为u(x).

②被积函数是幂函数和正(余)弦函数或幂函数和指数函数的乘积，就可考虑用分部积分法，并设幂函数为u(x).

③被积函数为三角函数与指数函数的乘积，可连续进行两次分部积分，均设三角函数为u(x)，得到一个所求积分满足的恒等式，从而求得积分.

为便于记忆和运用，关于分部积分法选u(x)的顺序可归纳为:“对、反、幂、三、指”.

4)有理函数、三角函数的有理式和简单无理函数的积分

有理函数是指具有如下形式的函数:

其中a₀≠0，b₀≠0.当n＜m时，称为真分式;当n≥m时，称为假分式.假分式可化成一个多项式与一个真分式之和.

有理函数积分的关键步骤是将真分式分解成部分分式之和，其分解方法如下:

设Q(x)=b₀(x－a)^α…(x－b)^β(x²+px+q)^λ…(x²+rx+s)^μ，其中p²－4q＜0，…，r²－4s

＜0，则真分式

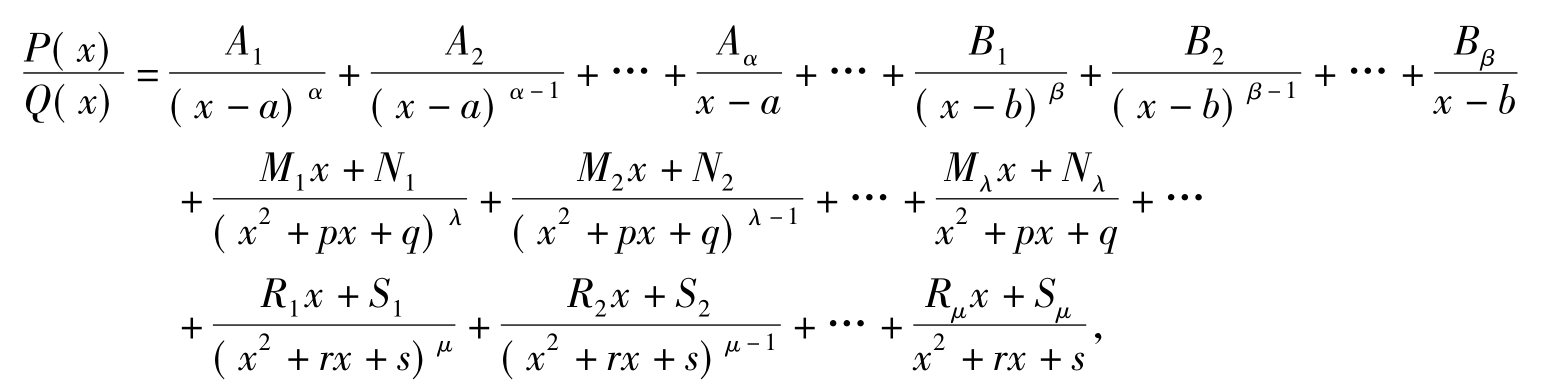
其中A_i，…，B_i，Mi，N_i，…，R_i，S_i等均为常数，其确定方法有以下两种.

方法一:等式两端去分母，比较等式两端x的同次幂的系数使之分别相等，将得出的等式求解.

方法二:在等式两端分别代入一些特殊的x值，得出若干个等式，然后将得出的等式求解.

三角函数有理式通过诱导公式都可化成sinx、cosx的有理式，记作R(sinx，cosx).作变换u=tan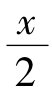，则

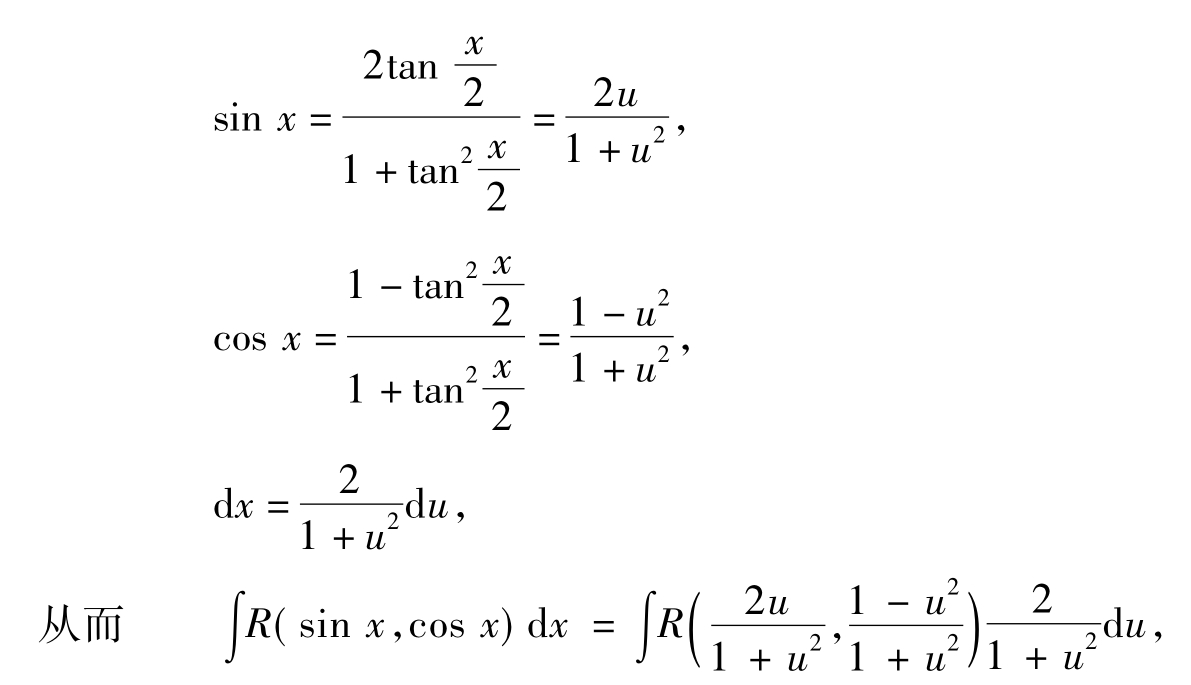
即通过变换u=tan，这种积分总可化为u的有理函数的积分，然后用有理函数的积分方法求解.但要注意，有时这种方法不一定简捷.

对于被积函数为R(x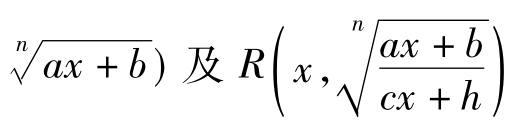，这两类函数的积分(其中R(x，u)表示x、u的有理函数)，可分别作变换:令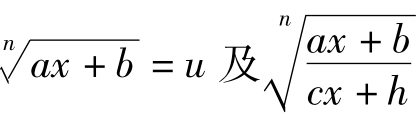=u，去掉根号，原积分就化为有理函数的积分.

【例1.3-1】求∫2cos2xdx.

解:令2x=u，得

∫2cos2xdx=∫cos2xd(2x)=∫cosudu=sinu+C=sin2x+C，

或

∫2cos2xdx=∫cos2xd(2x)=sin2x+C.其中C₁=C－lna.

【例1.3-7】求∫xlnxdx.

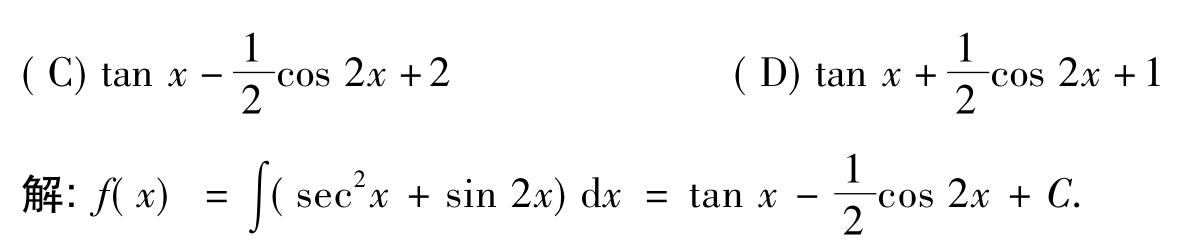
故选(C).

【例1.3-13】∫sin³xdx等于(　).

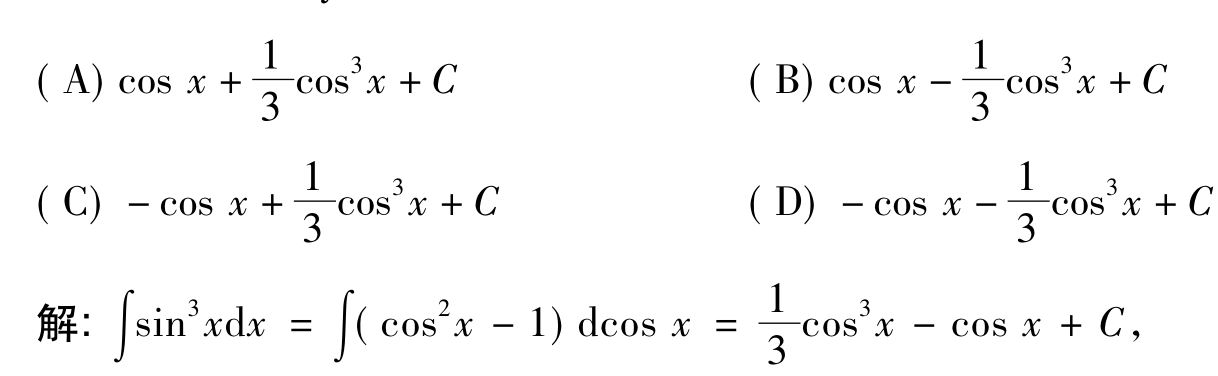
故选(C).

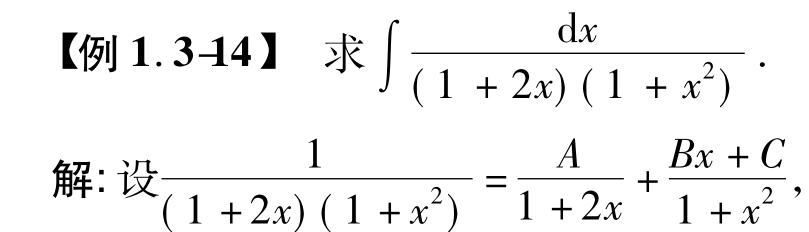
其中A、B、C为待定常数，其确定方法有

方法一:两端去分母，得

A(1+x²)+(Bx+C)(1+2x)=1，

即(A+2B)x²+(2C+B)x+(A+C)=1.

比较x的同次幂系数，得

A+2B=0，B+2C=0，A+C=1，

解得

方法二:两端去分母后，

令x=0，得A+C=1，

x=－1，得2A+B－C=1.

解得相同的A、B、C的值.

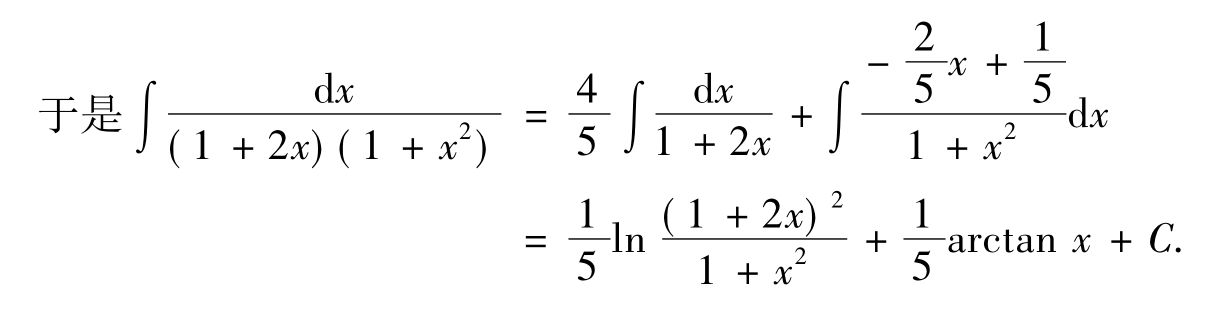
【例1.3-15】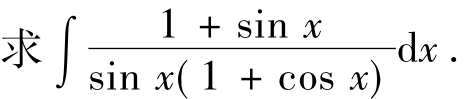

解:令u=tan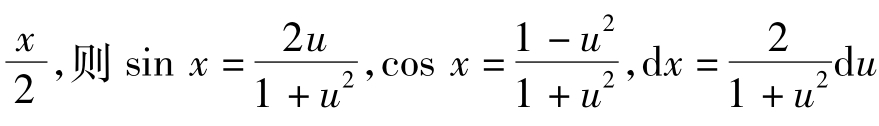，于是

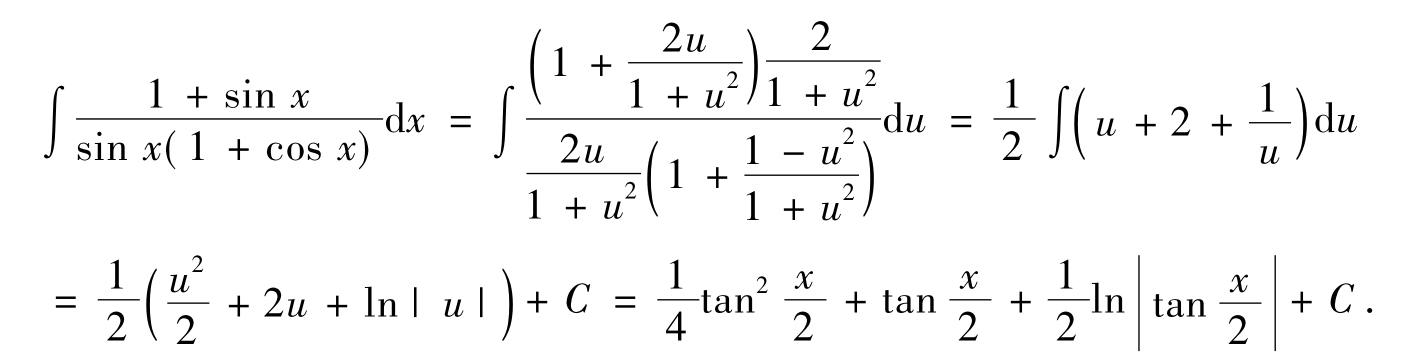
【例1.3-16】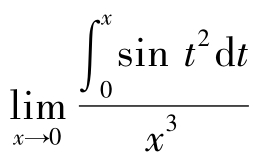等于(　).

解:利用洛必达法则及积分上限函数的导数公式，得

故选(B).

【例1.3-17】设I=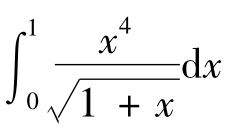，则估计I值的大致范围为(　).

(A)0≤I≤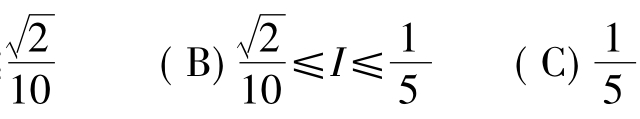＜I＜1(D)I≥1

解:因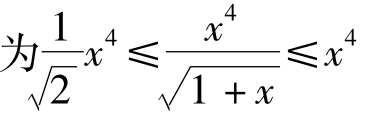(0≤x≤1)，所以

故选(B).

【例1.3-18】下列等式中，错误的是(　).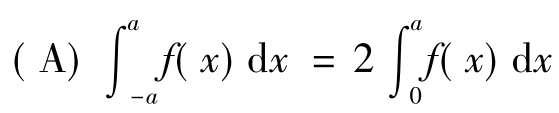，其中f(x)在［－a，a］(a＞0)上连续

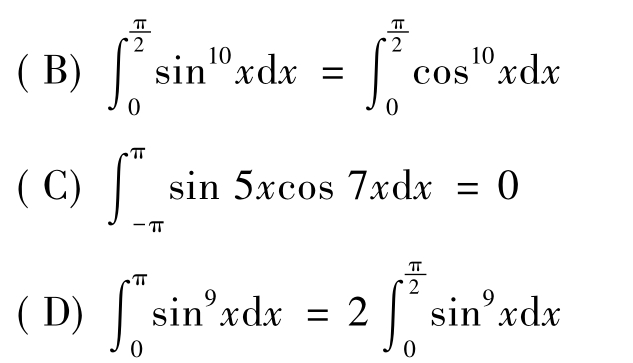
解:(B)、(C)、(D)三个等式都是正确的.事实上我们有以下更一般的结论:

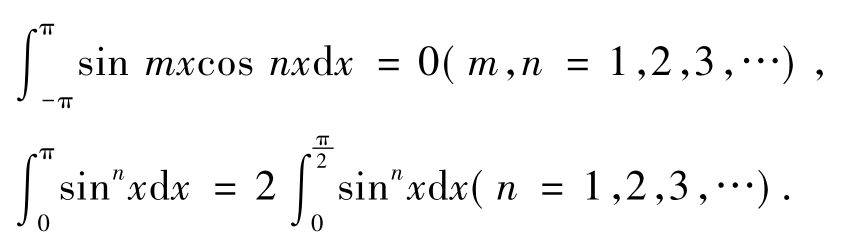
而等式(A)当f(x)为偶函数时成立，一般情形下未必成立，故选(A).