傅里叶级数

1.4.3　傅里叶级数

1.傅里叶级数概念

(1)三角函数系的正交性

三角函数系

1，cosx，sinx，cos2x，sin2x，…，cosnx，sinnx，…

在区间［－π，π］上正交，就是指上述三角函数系中任何不同的两个函数的乘积在区间［－π，π］上的积分等于零，即

(2)傅里叶系数和傅里叶级数

设f(x)是周期为2π的周期函数，且下面公式中出现的积分

都存在，则系数a₀，a₁，b₁，…叫做函数f(x)的傅里叶系数，级数

叫做函数f(x)的傅里叶级数.

(3)狄里克雷收敛定理

设f(x)是周期为2π的周期函数，若它满足条件:

①在一个周期内连续，或只有有限个第一类间断点;

②在一个周期内至多只有有限个极值点，则f(x)的傅里叶级数收敛，且当x是f(x)的连续点时，级数收敛于f(x);当x是f(x)的间断点时，级数收敛于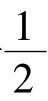［f(x⁺)+f(x^－)］.

2.正弦级数和余弦级数

(1)正弦级数

若f(x)是周期为2π的奇函数，则它的傅里叶系数为

a_n=0(n=0，1，2，…)，b_n=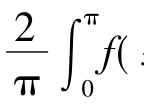x)sinnxdx(n=1，2，…)，

它的傅里叶级数是只含有正弦项的正弦级数

(2)余弦级数

若f(x)是周期为2π的偶函数，则它的傅里叶系数为

a_n=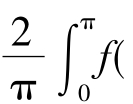x)cosnxdx(n=0，1，2，…)，

b_n=0(n=1，2，…)，

它的傅里叶级数是只含有常数项和余弦项的余弦级数

【例1.4-16】设f(x)是周期为2π的周期函数，它在［－π，π)上的表达式为

f(x)=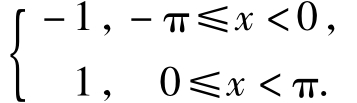

问f(x)的傅里叶级数在x=－π处收敛于何值.

解:所给函数满足狄里克雷收敛定理的条件，x=－π是函数的间断点，按收敛定理它的傅里叶级数在x=－π处收敛于

【例1.4-17】将函数f(x)=π²－x²(－π≤x≤π)展开成傅里叶级数.

解:将函数f(x)=π²－x²在［－π，π］外作周期延拓，注意到f(x)是偶函数，故b_n=0(n= 1，2，…).

f(x)满足收敛定理的条件，在［－π，π］上连续，且f(－π)=f(π)，因此在［－π，π］上，有

【例1.4-18】若f(－x)=g(x)，则f(x)与g(x)的傅里叶系数a_n，b_n，α_n，β_n(n=0，1，2，…)之间的关系为(　).

(A)a_n=α_n，b_n=β_n　　(B)a_n=α_n，b_n=－β_n

(C)a_n=－α_n，b_n=β_n　(D)a_n=－α_n，b_n=－β_n

解:因为

故选(B).

【例1.4-19】设f(x)是以2π为周期的周期函数，在［－π，π］上的表达式为f(x)=cos则f(x)的傅里叶级数为(　).

解:由于f(x)是偶函数，所以

因此，(A)、(D)是错误的.而(B)、(C)的差别只在于除常数项外的各项符号相反，所以，只需计算傅里叶系数a₁加以检验即可.

故选(C).

【例1.4-20】下列命题中，错误的是(　).

(A)设f(x)为奇函数，则f(x)的傅里叶级数是正弦级数

(B)设f(x)为偶函数，则f(x)的傅里叶级数是余弦级数

(C)设f(x)满足狄里克雷条件，则有

其中a_n，b_n为f(x)的傅里叶系数.

(D)设f(x)是周期为2π的周期函数，则f(x)的傅里叶系数为

解:若f(x)满足狄里克雷条件，则有

其中a_n，b_n是f(x)的傅里叶系数，而

因此命题(C)是错误的，应选(C).