一维随机变量的分布和数字特征

1.7.3　一维随机变量的分布和数字特征

随机变量是概率与数理统计中最重要、最基本的概念.一切随机现象都可以通过随机变量来描述.一维随机变量的取值范围(即样本空间)是实数轴(－∞，+∞)或它的一个子集，它总是一个数集.

1.随机事件及其概率的表达

与以往用A，B，C，…表达随机事件的形式不同，引进随机变量X，Y，Z，…之后，随机事件常常通过关于随机变量的等式或不等式来表达，例如，{a＜X≤b}，{a≤X≤b}，{a＜X＜b}，{a≤X＜b}，其中－∞≤a≤b≤+∞，一般地，随机事件总是可以表达成{X∈I}，其中数集I＞(－∞，+∞).

随机事件表达形式的改变使得事件的内涵丰富了.例如，由{|X|≤1}与{X＞2}的表达形式可知，这两个事件之间存在互不相容关系;由{|X|≤1}与{X=1}的表达形式可知，这两个事件之间存在包含关系;由{|X|≤1}与{|X|＞1}的表达形式可知，这两个事件之间存在对立关系.

如果两个随机变量X与Y相互独立，那么，对任意两个集合I₁，I₂＞(－∞，+∞)，随机事件{X∈I₁}与{Y∈I₂}总是相互独立的.

随着事件表达形式的改变，事件的概率相应地记作P(a＜X≤b)，P(a≤X≤b)，P(a＜X＜b)，P(a≤X＜b)，其中－∞≤a≤b≤+∞.一般地，事件的概率可以记作P(X∈I)，其中数集I＞(－∞，+∞).

2.一维随机变量的分布

引进随机变量之后，随机现象体现在随机变量取值的随机性上.通常称随机变量取值的统计规律性为随机变量的分布.掌握了一个随机变量的分布，也就能计算有关该随机变量的一切随机事件的概率P(X∈I)，其中I是任意一个数集，I＞(－∞，+∞).

随机变量分布的形式有3类:概率分布、概率密度函数与分布函数.概率分布仅适用于离散型随机变量，概率密度函数仅适用于连续型随机变量，分布函数则可用于一切随机变量.

(1)离散型随机变量的概率分布

离散型随机变量X只可能取有限个值或一串值，以下记作x₁，x₂，…，x_k，….X的概率分布可以用表格形式来表达，通常称为概率分布(表).X的概率分布表为

其中{x₁，x₂，…，x_k，…}是X的取值范围，一般按从小到大(沿数轴方向)排列;p_k=P(X=x_k)

＞0，k=1，2，…，它们必定满足=1.

概率分布表中诸事件{X=x_k}，k=1，2，…构成一个完备事件组.因此，由概率分布表可以计算任意随机事件的概率:

其中数集I＞(－∞，+∞).

(2)连续型随机变量的概率密度函数

连续型随机变量X的取值范围通常是一个区间或若干区间之并.X的概率密度函数p(x)是定义域为(－∞，+∞)的实值函数，它必须满足

①p(x)≥0，－∞＜x＜+∞.

②x)dx=1.

连续型随机变量的取值范围可以理解成{x|p(x)＞0}.

由概率密度函数p(x)可以计算任意随机事件的概率:

P(X∈I)=∫_Ip(x)dx，

其中数集I＞(－∞，+∞).

由上述概率计算公式知道，对于连续型随机变量

P(X=x₀)=0，

其中x₀是任意一个实数.这里要注意，事件{X=x₀}≠Φ，因为{X=x₀}是可能发生的.这个特性是离散型随机变量所不具有的.由此还可得到:

P(a＜X≤b)=P(a≤X≤b)=P(a＜X＜b)=P(a≤X＜b)=x)dx，

其中－∞≤a＜b≤+∞.

(3)随机变量的分布函数

对于一切随机变量X，X的分布函数定义为

F(x)=P(X≤x)，－∞＜x＜∞.

分布函数F(x)是定义域为(－∞，+∞)的实值函数.

分布函数必定具有下列四条特征性质.

①有界性:0≤F(x)≤1，－∞＜x＜+∞.

②单调性:当x₁＜x₂时，F(x₁)≤F(x₂).

③右连续:x)=F(x₀).

④F(x)=1.

反过来，如果一个定义域为(－∞，+∞)的实值函数具有上述四条性质，那么F(x)必定是某个随机变量的分布函数.

由分布函数F(x)可以计算任意随机事件的概率:

P(a＜X≤b)=F(b)－F(a)，

P(X=x₀)=F(x)

其中－∞≤a＜b≤+∞，x₀是任意实数.例如，

P(1≤X≤2)=P(1＜X≤2)+P(X=1)=［F(2)－F(1)］+［F(1)－x)］

由此看出，利用分布函数计算概率在实际操作中是比较麻烦的.因此，在知道离散型随机变量的概率分布或连续型随机变量的概率密度函数时，建议不要用分布函数计算概率，要用概率分布或概率密度函数来计算.

当X是离散型随机变量时，按分布函数的定义，由概率分布可以计算分布函数:

F(x)=，－∞＜x＜+∞.

这是一个阶梯状的函数，且在x=x_k有跳跃间断点，跳跃度恰是p_k.当x≠x_k时，F(x)在该处连续.

当X是连续型随机变量时，按分布函数的定义，由概率密度函数可以计算分布函数:

F(x)=t)dt，－∞＜x＜+∞.

由高等数学中积分上限函数的知识推得:连续型随机变量的分布函数是连续函数，而不仅仅是右连续函数，且在p(x)的连续点处，

F'(x)=p(x).

因此，连续型随机变量的分布函数F(x)本质上是其概率密度函数p(x)的一个原函数.这些特性对离散型随机变量不适用.

(4)常用随机变量的分布

常用的离散型随机变量有三类.

①二点分布(或伯努利分布)

参数为p(0＜p＜1)的二点分布的概率分布表为

二点分布的取值范围是{0，1}，且规定p=P(X=1).

二点分布是伯努利试验的数量化表示.伯努利试验中试验结果“成功”与“X=1”对应，试验结果“失败”与“X=0”对应.因此，随机变量X表示一次伯努利试验后出现成功的次数.

②二项分布

参数为n，p(n是自然数，0＜p＜1)的二项分布的概率分布为

二项分布的取值范围是{0，1，…，n}.

服从参数为n，p的二项分布的随机变量X表示:重复独立地做n次伯努利试验后出现成功的次数.

③泊松分布

参数为λ(λ＞0)的泊松分布的概率分布为

P(X=k)=e，k=0，1，2，….

泊松分布的取值范围是{0，1，2，…}.

常用的连续型随机变量有三类.

①均匀分布

参数为a，b(－∞＜a＜b＜+∞)的均匀分布的概率密度函数为

分布函数为

②指数分布

参数为λ(λ＞0)的指数分布的概率密度函数为

分布函数为

③正态分布

参数为μ，σ²(－∞＜μ＜+∞，σ＞0)的正态分布的概率密度函数为

正态分布通常用记号N(μ，σ²)表示.当μ=0，σ²=1时，称N(0，1)为标准正态分布.

当X服从N(0，1)时，分布函数记为Φ(x)，即

Φ(x)的值可以查表得到.Φ(x)满足

①“a＜x＜b”也可以写成“a≤x≤b”，因为这不会影响积分.连续型随机变量的概率密度函数都有这个特点.

②“a≤x＜b”也可以写成“a≤x≤b”，因为F(x)是连续函数.连续型随机变量的分布函数都有这个特点.

Φ(－x)=1－Φ(x)，－∞＜x＜+∞.

Φ(x)的这两条性质是由其概率密度函数为偶函数决定的.一般地，对任意一个连续型随机变量，只要它的概率密度函数p(x)是偶函数，那么，其分布函数F(x)必定满足

F(－x)=1－F(x)，－∞＜x＜+∞.

当X服从标准正态分布N(0，1)时，任意事件的概率

P(a＜X≤b)=Φ(b)－Φ(a)，－∞≤a＜b≤+∞.

由于Φ(x)是分布函数，因此Φ(－∞)=0，Φ(+∞)=1.上式对P(a≤X≤b)，P(a＜X＜b)，P(a≤X＜b)同样成立.

当X服从正态分布N(μ，σ²)时，X的分布函数为

任意事件的概率

定理1如果X服从正态分布N(μ，σ²)，那么Y=kX+c服从正态分布N(kμ+c，k²σ²).特殊地，服从标准正态分布N(0，1).

定理表明正态随机变量的线性函数依然服从正态分布.称为标准化变换，其意义见下面随机变量的数字特征.

3.一维随机变量的数字特征

随机变量的分布全面反映了随机变量取值的统计规律性，随机变量的数字特征则局部地反映随机变量取值的某些主要特征.随机变量的数字特征的含义是:用某些实数来反映随机变量分布的主要特征.

随机变量数字特征的常用形式有三类:数学期望、方差与标准差.

(1)数学期望

随机变量X的数学期望反映了X的平均取值，记作E(X).

当X为离散型随机变量时，如果X的概率分布表为

那么规定X的数学期望为

规定随机变量函数Y=f(X)的数学期望为

当X为连续型随机变量时，如果X的概率密度函数为p(x)，那么规定X的数学期望为

规定随机变量函数Y=f(X)的数学期望为

数学期望有下列性质:

①E(c)=c，其中c是常数;

②E(kX)=kE(X)，其中k是常数;

③E(X+c)=E(X)+c，其中c是常数;

④E(kX+lY+c)=kE(X)+lE(Y)+c，其中k，l，c是常数;

⑤当X与Y相互独立时，E(XY)=E(X)E(Y).

解题时一般用数学期望的性质比较方便，但要注意上述性质适用的条件.

(2)方差与标准差

随机变量的方差与标准差都反映了随机变量取值相对于其数学期望的波动程度.D(X)表示随机变量X的方差，表示随机变量X的标准差.

对于任意一个随机变量X，规定X的方差为

D(X)=E［X－E(X)］².

方差的常用计算公式为

D(X)=E(X²)－［E(X)］².

这个公式表明，计算方差的基础是计算数学期望.

方差有下列性质:

①D(c)=0，其中c是常数;

②D(kX)=k²D(X)，其中k是常数;

③D(X+c)=D(X)，其中c是常数;

④当X与Y相互独立时，

D(kX+lY+c)=k²D(X)+l²D(Y)，其中k，l，c是常数.

使用方差的性质要仔细.例如，当D(X)=2时，D(－X)=(－1)²×2=2，而不是D(－X)=－D(X).方差D(X)≥0，且方差D(X)=0的充分必要条件是X为常数，即

P(X=c)=1，

其中c=E(X).

(3)中心化与标准化

给定随机变量X，称X_*=X－E(X)为X的中心化随机变量，称X^*=为X的标

准化随机变量.由数学期望与方差的性质得到:

E(X_*)=0，D(X_*)=D(X);

E(X^*)=0，D(X^*)=1.

如果某个连续型随机变量X的概率密度函数关于x=μ对称，那么，当X的数学期望存在时必定有E(X)=μ.

(4)常用随机变量的数字特征

常用随机变量的数字特征可以作为已知值直接使用.

①当X服从参数为p的二点分布时，

E(X)=p，D(X)=p(1－p).

②当X服从参数为n，p的二项分布时，

E(X)=np，D(X)=np(1－p).

③当X服从参数为λ的泊松分布时，

E(X)=λ，D(X)=λ.

④当X服从参数为a，b的均匀分布时，

⑤当X服从参数为λ的指数分布时，

⑥当X服从参数为μ，σ²的正态分布N(μ，σ²)时，

E(X)=μ，D(X)=σ²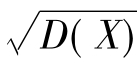，=σ.

定理1表明，当X服从N(μ，σ²)时，标准化随机变量X^*服从N(0，1).

定理2设随机变量X与Y相互独立，X服从正态分布N(μ₁，σ²₁)，Y服从正态分布N(μ₂，σ²₂)，那么Z=kX+lY+c服从正态分布N(kμ₁+lμ₂+c，k²σ²₁+l²σ²₂).

定理2是定理1的推广形式，它表明独立正态随机变量的线性函数依然服从正态分布.【例1.7-11】设X是随机变量，已知P(X≤1)=p，P(X≤2)=q，则P(X≤1，X≤2)等于(　).

(A)p+q　(B)p－q　(C)q－p　(D)p

解:由于随机事件{X≤1}＞{X≤2}，因此

P(X≤1，X≤2)=P(X≤1)=p.

故选(D).

用随机变量表达随机事件时，注意

{X≤1，X≤2}={X≤1}∩{X≤2}.

这是一种规定的表示方法.

【例1.7-12】设随机变量X与Y相互独立，已知P(X≤1)=p，P(Y≤1)=q，则P(max(X，Y)≤1)等于(　).

(A)p+q　(B)pq　(C)p　(D)q

解:随机事件

{max(X，Y)≤1}={X≤1，Y≤1}，

因此，由乘法公式得到

P(max(X，Y)≤1)=P(X≤1，Y≤1)=P(X≤1)P(Y≤1)=pq.

故选(B).

本题中{max(X，Y)≤1}可以分解成两个简单事件的积，类似地，

{max(X，Y)≥1}={X≥1}∪{Y≥1}，

{min(X，Y)≥1}={X≥1，Y≥1}，

{min(X，Y)≤1}={X≤1}∪{Y≤1}.

例如，由本题所给条件可以算得(按加法公式与乘法公式):

P(min(X，Y)≤1)=P({X≤1}∪{Y≤1})=P(X≤1)+P(Y≤1)－P(X≤1，Y≤1)

=p+q－P(X≤1)P(Y≤1)=p+q－pq.

读者要习惯随机事件用随机变量的等式或不等式来表达的形式.

【例1.7-13】设离散型随机变量X的概率分布表为

试求:(1)常数c;

(2)概率P(X²＜π);

(3)分布函数值F(1);

(4)分布函数F(x).

解:(1)由于概率分布表中诸p_k必须满足=1，因此，由

0.1+0.2+0.3+c=1，

推得c=0.4.

(2)X的取值范围是{－1，0，1，3}.这些值中满足不等式＜π”的是－1，0，1.因此

P(X²＜π)=P(X=－1)+P(X=0)+P(X=1)=0.1+0.2+0.3=0.6.

(3)按分布函数的定义，

F(1)=P(X≤1)=P(X=－1)+P(X=0)+P(X=1)=0.6.

(4)按分布函数的定义作如下逐段讨论:

当x＜－1时，

F(x)=P(X≤x)=P(Φ)=0;

当－1≤x＜0时，

F(x)=P(X≤x)=P(X=－1)=0.1;

当0≤x＜1时，

F(x)=P(X≤x)=P(X=－1)+P(X=0)=0.1+0.2=0.3;

当1≤x＜3时，

F(x)=P(X≤x)=P(X=－1)+P(X=0)+P(X=1)=0.1+0.2+0.3=0.6;

当x≥3时，

F(x)=P(X≤x)=P(Ω)=1.

把上述结果综合起来，得到分段函数形式表达的分布函数:

【例1.7-14】设离散型随机变量X的分布函数为

试求:(1)X的概率分布表;

(2)关于t的一元二次方程Xt²－2t+1=0有两个不同实根的概率.

解:(1)F(x)仅在x=－1，0，1处间断，且是跳跃间断点，跳跃度分别是0.2，0.6，0.2.因此，X的概率分布表为

(2)一元二次方程的判别式Δ=4－4X.注意到二次项系数不能为0，因此所求概率为

P(Δ＞0，X≠0)=P(4－4X＞0，X≠0)=P(X＜1，X≠0)=P(X=－1)=0.2.

这里出现的概率也可以用分布函数计算:

P(X=－1)=F(－1)－=0.2－0=0.2.

【例1.7-15】设连续型随机变量X的概率密度函数为

试求:(1)常数c;

(2)概率

(3)分布函数值

(4)分布函数F(x).

解:(1)由于概率密度函数p(x)必须满足x)dx=1.因此，由

推得

(2)由高等数学中分段函数的积分得到

(3)按分布函数的定义

(4)按分布函数的定义作如下逐段讨论:

当x＜－1时，

当－1≤x＜1时，

当x≥1时，

把上述结果综合起来，得到分段函数形式表达的分布函数:

【例1.7-16】设连续型随机变量X的分布函数

试求:(1)X的概率密度函数;

(2)条件概率P(X＞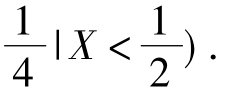

解:(1)按高等数学中分段函数的求导规则，当x＜0或x＞1时，p(x)=F'(x)=0;当0＜x＜1时，p(x)=F'(x)=2x.于是，X的概率密度函数为

这里要注意，与高等数学中分段函数分段点(本例中x=0与x=1)求导规则不同，在概率中不需要用导数的定义去求，而是自动纳入“其他”类中.这不会影响今后对概率密度函数p(x)作积分.

(2)由条件概率计算公式得到

这里出现的概率也可以用分布函数计算:

【例1.7-17】设随机变量X服从正态分布N(1，4).已知Φ(1)=a，则P(－1＜X≤3)等于(　).

(A)a－1　(B)2a+1　(C)a+1　(D)2a－1

解:按正态分布的概率计算公式(μ=1，σ=2)，则

P(－1＜X≤3)=Φ=Φ(1)－Φ(－1)=Φ(1)－［1－Φ(1)］

=2Φ(1)－1=2a－1.

故选(D).

【例1.7-18】设随机变量X服从正态分布N(μ，1).已知P(X≤μ－3)=c，则P(μ＜X＜μ+3)等于(　).

(A)2c－1　(B)1－c　(C)0.5－c　(D)0.5+c解:由于

P(X≤μ－3)=Φ((μ－3)－μ)=Φ(－3)=c，

因此，

P(μ＜X＜μ+3)=Φ((μ+3)－μ)－Φ(μ－μ)=Φ(3)－Φ(0)

=［1－Φ(－3)］－0.5=(1－c)－0.5=0.5－c.

故选(C).

【例1.7-19】设随机变量X服从正态分布N(－1，9)，则随机变量Y=2－X服从(　).

(A)正态分布N(3，9)　(B)均匀分布

(C)正态分布N(1，9)　(D)指数分布

解:按定理1，Y是X的线性函数，Y依然服从正态分布.由k=－1、c=2算得Y服从正态分布

N(2－(－1)，(－1)²×9)=N(3，9).

故选(A).

【例1.7-20】把一颗均匀骰子掷了6次，假定各次出现的点数相互不影响.随机变量X表示出现6点的次数，则X服从(　).

解:每掷一次骰子可以看成做一次伯努利试验，把“出现6点”看做“成功”，把“不出现6点”看做“失败”.独立地掷6次骰子相当于重复独立地做6次伯努利试验，且一次伯努利试验后出现成功的概率p=，故选(C).

如果把“出现6点”看做“失败”，把“不出现6点”看做“成功”，那么p=因此，也可以认为随机变量X服从参数n=6，p=的二项分布.

【例1.7-21】设离散型随机变量X的概率分布表为

试求:(1)X的数学期望、方差与标准差;

(2)E

(3)E(3X²－2).

解:(1)按数学期望的定义，则

E(X)==(－2)×0.5+1×0.1+2×0.3+5×0.1=0.2.

按随机变量函数的数学期望的定义，则

E(X²)==(－2)²×0.5+1²×0.1+2²×0.3+5²×0.1=5.8.

于是，由方差的计算公式得到

D(X)=E(X²)－［E(X)］²=5.8－0.2²=5.76.

(2)按随机变量函数的数学期望的定义，则

(3)由(1)中得到的E(X²)=5.8及数学期望的性质得到

E(3X²－2)=3E(X²)－2=3×5.8－2=15.4.

【例1.7-22】设连续型随机变量X的概率密度函数为

试求:(1)X的数学期望、方差与标准差;

解:(1)按数学期望的定义，则

按随机变量函数的数学期望的定义，则

于是，由方差的计算公式得到

D(X)=E(X²)－［E(X)］²=2－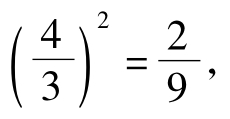

(2)按随机变量函数的数学期望的定义，则

(3)由(1)与(2)中得到的结果及数学期望的性质得到

【例1.7-23】某人独立地射击10次，每次射击命中目标的概率为0.8，随机变量X表示10次射击中命中目标的次数，则E(X²)等于(　).

(A)64　(B)65.6　(C)66.6　(D)80

解:把每次射击看成是做一次伯努利试验，“成功”表示“命中目标”，“失败”表示“没有命中目标”，出现成功的概率p=0.8.于是，X服从参数n=10，p=0.8的二项分布.已知二项分布的数学期望与方差分别是

E(X)=np=10×0.8=8，

D(X)=np(1－p)=10×0.8×0.2=1.6.

于是，由方差的计算公式推得

E(X²)=D(X)+［E(X)］²=1.6+8²=65.6.

故选(B).

本题借助于常用分布的数字特征来求E(X²)是比较方便的，因为常用分布的数学期望与方差可以作为已知值使用.如果用随机变量函数的数学期望的定义，即

E(X²)=×0.8^k×0.2^10－k，

则加法不易计算.

【例1.7-24】设随机变量X服从区间(－1，5)上的均匀分布，Y=3X－5，则E(Y)与D(Y)分别等于(　).

(A)1，9　(B)3，27　(C)4，27　(D)1，27

解:已知区间(－1，5)上的均匀分布的数学期望与方差分别是

于是，由数学期望与方差的性质得到

E(Y)=E(3X－5)=3E(X)－5=3×2－5=1，

D(Y)=D(3X－5)=3²D(X)=3²×3=27.

故选(D).

【例1.7-25】设随机变量X与Y相互独立，它们分别服从参数λ=2的泊松分布与指数分布.记Z=X－2Y，则随机变量Z的数学期望与方差分别等于(　).

(A)1，3　(B)－2，4　(C)1，4　(D)－2，6

解:已知参数λ=2的泊松分布的数学期望与方差分别为

E(X)=2，D(X)=2;

参数λ=2的指数分布的数学期望与方差分别为

由数学期望与方差的性质得到

E(Z)=E(X－2Y)=E(X)－2E(Y)=2－2×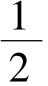=1，

D(Z)=D(X－2Y)=D(X)+(－2)²D(Y)=2+4×=3.

故选(A).

【例1.7-26】已知某个连续型随机变量X的数学期望E(X)=1，则X的概率密度函数不可能是(　).

解:(A)、(C)、(D)的概率密度函数p(x)都关于直线x=1对称，而(B)的概率密度函数p(x)是偶函数，即关于直线x=0对称.因此，如果数学期望存在，那么(B)情形下E(X)=0，故选(B).

本题如果分别直接计算数学期望，那么耗时又费力.用对称性来判断则方便得多.