随机变量协方差定义

1.7.4　矩、协方差与相关系数

除了随机变量的数学期望、方差与标准差之外，有用的数字特征还有矩、协方差与相关系数.但是，它们有些涉及两个随机变量.

1.矩

随机变量幂函数的数学期望统称为矩.

给定随机变量X，称E(X^k)为X的k阶原点矩，称E(X－EX)^k为X的k阶中心矩，其中k为正整数.

数学期望E(X)是X的一阶原点矩，方差D(X)是X的二阶中心矩.

矩在数理统计的点估计中有重要应用.

2.两个随机变量函数的数学期望

给定两个随机变量X与Y，随机变量Z=f(X，Y).

当离散型随机变量X与Y的联合概率分布为P(X=x_i，Y=y_j)=p_ij(i、j=1，2，…)时，

E(Z)=Ef(X，Y)=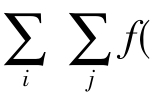x_i，y_j)p_ij

当连续型随机变量X与Y的联合概率密度函数为p(x，y)时，

E(Z)=Ef(X，Y)=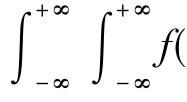x，y)p(x，y)dxdy.

3.协方差

给定两个随机变量X与Y.规定X与Y的协方差

Cov(X，Y)=E［(X－EX)(Y－EY)］

协方差的常用计算公式为

Cov(X，Y)=E(XY)－E(X)E(Y).

协方差有下列性质:

①Cov(X，X)=D(X)，Cov(X，Y)=Cov(Y，X);

②Cov(X，c)=0;

③Cov(kX，lY)=klCov(X，Y);

④Cov(X₁±X₂，Y)=Cov(X₁，Y)±Cov(X₂，Y);

⑤当X与Y相互独立时，Cov(X，Y)=0.

4.相关系数

给定两个随机变量X与Y.规定X与Y的相关系数

当ρ(X，Y)=0时，称X与Y不相关.

相关系数有下列性质:

①|ρ(X，Y)|≤1;

②当X与Y相互独立时，X与Y必定不相关.但反之一般不成立;

③D(X±Y)=D(X)+D(Y)±2ρ(X，Y)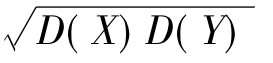

=D(X)+D(Y)+2Cov(X，Y).

【例1.7-27】设离散型随机变量X与Y的联合概率分布表为

试求:(1)E(XY);

(2)Cov(X，Y)与ρ(X，Y).

解:(1)E(XY)=0×0×0+0×1×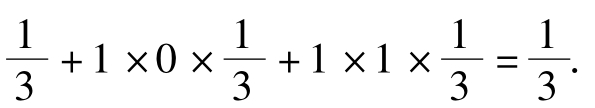

(2)由E(X)=0×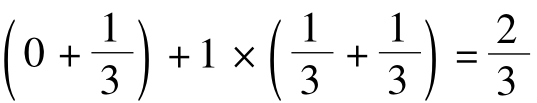=E(Y)及(1)中算得的结果推出

Cov(X，Y)=E(XY)－E(X)E(Y)=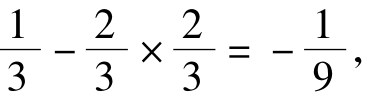

由D(X)=E(X²)－(EX)²==D(Y)得到

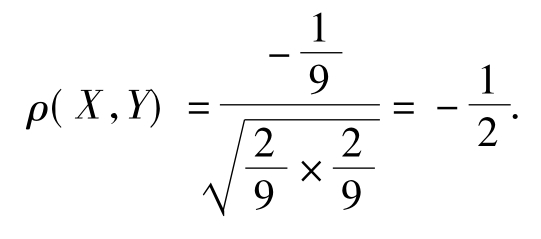
【例1.7-28】设连续型随机变量X与Y的联合概率密度函数为

试求:(1)E(XY);

(2)Cov(X，Y)与ρ(X，Y).

从而ρ(X，Y)=0.这表明X与Y不相关.

【例1.7-29】已知D(X)=2，D(Y)=3，则Cov(X+Y，X－Y)等于(　).

(A)1　(B)－1　(C)5　(D)6

解:由协方差的性质④得到

Cov(X+Y，X－Y)

=Cov(X，X)－Cov(X，Y)+Cov(Y，X)－Cov(Y，Y)

=D(X)－D(Y)=2－3=－1.

故选(B).

【例1.7-30】已知D(X)=4，D(Y)=9，Cov(X+Y)=2，则D(3X－2Y)等于(　).

(A)96　(B)72　(C)48　(D)36

解:由相关系数的性质③推得

D(3X－2Y)=D(3X)+D(2Y)－2Cov(3X，2Y)

=9D(X)+4D(－Y)－2×3×2Cov(X，Y)

=9×4+4×9－12×2=48.

故选(C).