参数估计的未知参数是什么

1.7.6　参数估计——点估计

根据样本X₁，…，X_n对总体X中所含未知参数θ进行估计，这就是参数估计.

对于未知参数θ，用某个实数来估计，这称为点估计.未知参数θ的点估计记作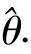.由于样本的意义具有双重性，因此，在随机抽样前，求点估计即是构造估计量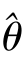=f(X₁，…，X_n);在随机抽样后，把样本值(即数据)代入估计量公式便得θ的估计值.

1.矩估计

矩估计的原理是用样本原点矩来估计相应(即同阶)的总体原点矩(假如是未知的).

当E(X)，D(X)未知时，E(X)的矩估计是样本均值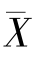，D(X)的矩估计是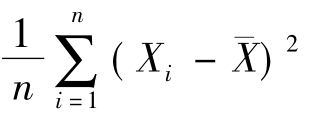(不是样本方差S²)，(不是样本标准差S).

2.最大似然估计

设总体X是连续型随机变量，它的概率密度函数记作p(x;θ)，其中θ是未知参数，这里用p(x;θ)取代概率中使用的p(x)，这是为了强调存在未知参数θ，因为θ是估计的对象.如果总体X是离散型随机变量，今后仍用p(x;θ)表示概率分布，它的含义是

p(x;θ)=P(X=x)，x=x₁，x₂，…

这样“总体X的分布为p(x;θ)”既包含了连续型随机变量，也包含了离散型随机变量.例如，总体X服从参数为λ的泊松分布，那么X的概率分布可以表示成

设总体X的分布为p(x;θ)，其中θ是未知参数.称

为似然函数.如果^θ满足

那么称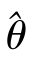是θ的最大似然估计.由于L(θ)中含有x₁，…，x_n，因此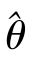必定是样本x₁，…，x_n的函数.随机抽样后，可以计算出未知参数的点估计值.

求最大似然估计可以按下列步骤进行:

①计算似然函数L(θ);

②计算似然函数的对数lnL(θ);

③求导数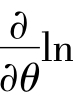L(θ);

④解似然方程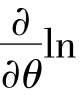L(θ)=0.

似然方程的解便是θ的最大似然估计.只要似然方程的解是唯一的，不需要像高等数学中那样去验证充分条件，因为它必定使似然函数达到最大.另外，求导数中采用偏导数记号是为了强调除了未知参数θ是求导变量外，其余变量都视为常数.

3.估计量的评选标准

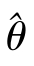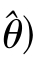当未知参数θ的估计量满足E(=θ时，称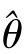是θ的无偏估计.

当^θ^*与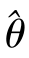都是未知参数θ的无偏估计，且D(^θ^*)＜D(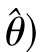时，称^θ^*比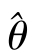有效.

【例1.7-34】设总体X是连续型随机变量，X的概率密度函数为

其中θ＞0，θ是未知参数.X₁，…，X_n是取自总体X的样本.试求:

(1)θ的矩估计;

(2)θ的最大似然估计.

解:(1)由于总体X的数学期望

因此，θ=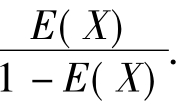按照矩估计的原理，E(X)用样本均值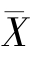估计，从而得到θ的矩估计=

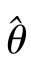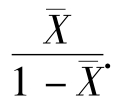
(2)似然函数L(θ)=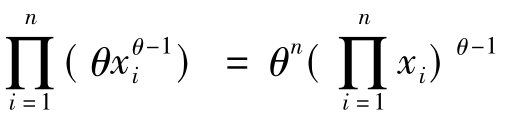.于是，由

lnL(θ)=nlnθ+(θ－1)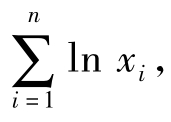

解得θ=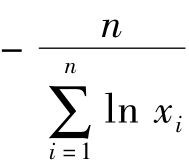

，即θ的最大似然估计=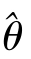

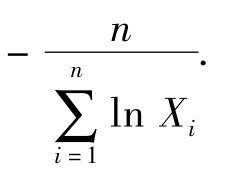
【例1.7-35】设总体X服从参数为λ的泊松分布，其中λ未知.X₁，…，X_n是取自总体X的样本，则λ的最大似然估计是(　).

(A)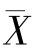　(B)S²　(C)S　(D)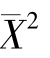

解:似然函数

于是，由

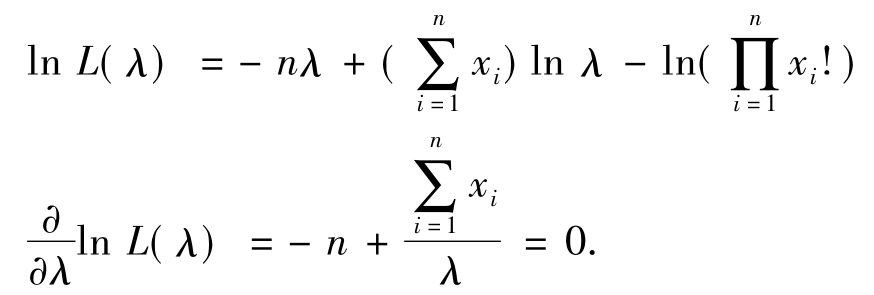
解得λ的最大似然估计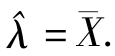.故选(A).

【例1.7-36】设X₁，…，X_n是取自正态总体N(μ，1)的样本，其中μ未知.μ的无偏估计是(　).

(A)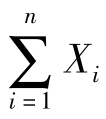　(B)S²　(C)0.4X₁+0.6X_n　(D)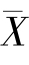－X₁

解:算得E(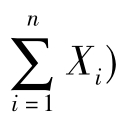=nμ(数学期望性质④)，E(S²)=1(定理3②)，E(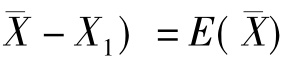－E(X₁)=μ－μ=0(定理3①)，但

E(0.4X₁+0.6X_n)=0.4E(X₁)+0.6E(X_n)=0.4μ+0.6μ=μ.

故选(C).

【例1.7-37】设X₁，…，X_n是取自正态总体N(μ，1)的样本，其中μ未知.下列μ的无偏估计中，最有效的是(　).

解:由方差的性质④算得

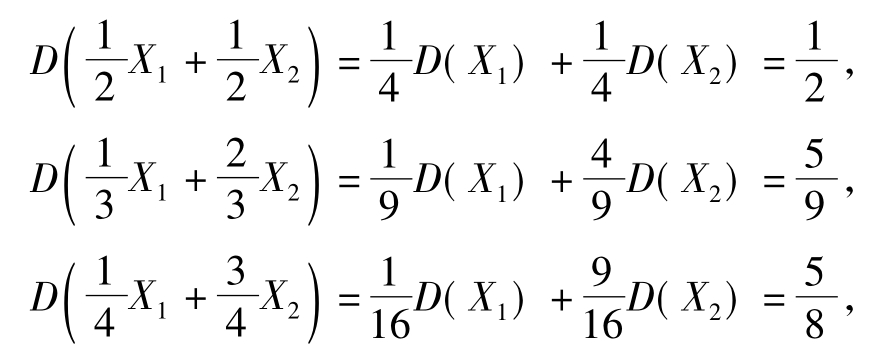
而D(X₁)=1.故选(A).