【摘要】：理想气体是实际气体的一个抽象化模型。宏观上讲，当密度不太高、压强不太大以及温度不太低时，能够严格遵从三个实验定律的气体定义为理想气体。总之，气体可看作自由地、无规则地运动着的弹性球分子的集合，这是理想气体的微观模型。当一定质量的理想气体从状态Ⅰ变化到状态Ⅱ时，两状态之间的关系为式中:n=为单位体积分子数，其中N是分子总数;k==1.38×10－23 J/K，称为玻耳兹曼常数，其中NA=6.023×1023/mol，称为阿伏加德罗常数。
2.1.3 理想气体状态方程
1.理想气体
理想气体是实际气体的一个抽象化模型。宏观上讲，当密度不太高、压强不太大以及温度不太低时，能够严格遵从三个实验定律(即玻意耳—马略特定律、盖—吕萨克定律和查理定律)的气体定义为理想气体。从微观角度可对理想气体作如下描述:①气体分子的大小与气体分子间的距离相比较可以忽略不计;②气体分子处在无规则的热运动中且服从经典力学规律;③除碰撞的瞬间外，分子所受作用力可以忽略，而且分子之间以及分子与器壁之间的碰撞是弹性的，动量与动能均守恒。总之，气体可看作自由地、无规则地运动着的弹性球分子的集合，这是理想气体的微观模型。
2.理想气体状态方程
当一定质量的理想气体从状态Ⅰ(p1、V1、T1)变化到状态Ⅱ(p2、V2、T2)时，两状态之间的关系为
这是理想气体状态方程的一种形式。
质量为M、摩尔质量为μ的理想气体处在某平衡态下时，各状态参量间的关系为
式中:p的单位为Pa;V的单位为m3;T的单位为K;R=8.31J/(mol·K)称为普适气体常量。
这是理想气体状态方程的常用形式，其中的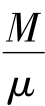
是摩尔数。
由上述常用形式还可以导出理想气体状态方程的另一种形式为
式中:n=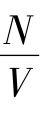
为单位体积分子数(即分子数密度)，其中N是分子总数;k=
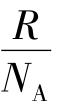=1.38×10－23 J/K，称为玻耳兹曼常数，其中NA=6.023×1023/mol，称为阿伏加德罗常数。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
