麦克斯韦速率分布律

2.1.8　麦克斯韦速率分布律

1.麦克斯韦速率分布函数

气体中的大量分子在永不停息的热运动中频繁碰撞，彼此交换能量，速率在不断地改变。在平衡态下，速率处于各个区间中的分子数服从确定的统计规律。设分子总数为N，速率处于v～v+Δv区间中的分子数为ΔN，其在分子总数中所占百分比为不但与区间宽度Δv有关，而且与区间Δv所处的速率v有关。当Δv→0时，是速率v的连续函数，记为f(v)。麦克斯韦应用统计理论给出了f(v)的具体表达式为

此式称为气体分子的麦克斯韦速率分布函数。速率分布函数f(v)的物理意义如下:对大量气体分子而言，f(v)表示分布在速率v附近，单位速率间隔内的分子数占总分子数的百分比;对单个分子而言，f(v)表示分子速率处于v附近，单位速率间隔内的概率。即函数f(v)表示概率密度。

图2.1-1

麦克斯韦速率分布曲线如图2.1-1所示。

在横轴上的速率v处，取小区间v～v+dv，则f(v)dv=对应f(v)曲线下dv宽度内的面积，数值上等于v～v+dv区间内的分子数占总分子数的百分比。将区间扩大为v₁～v₂，则积分对应f(v)曲线下v₁～v₂区间内的面积，数值上等于v₁～v₂区间内的分子数ΔN占总分子数的百分比。如将区间进一步扩大为0～∞，则积分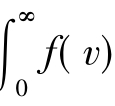dv对应f(v)曲线下的全部面积，数值上等于0～∞区间内的分子数占总分子数的百分比，其值为百分之百，所以有

此式称为速率分布函数的归一化条件。

应该指出，除了讨论速率分布之外，针对不同的用途，还可以讨论其他物理量的分布，例如分子自由程分布等，不同分布函数的表达式不同，但其共同点是均要满足归一化条件。

2.气体分子热运动的三种速率

(1)最概然速率v_p

最概然速率是指f(v)曲线峰值对应的速率。由f(v)的物理意义可知，在此速率附近，单位速率间隔内的分子百分数最大。令=0，可得

将此式代入到f(v)中，得f(v_p)。可见，对同一气体而言，温度T越高，v_p值越大，而f(v)曲线峰值越小。由于受归一化条件限制，f(v)曲线下的总面积为定值，曲线峰值减小，必然使得曲线横向较宽。如图2.1-2所示。另一方面，对相同温度下的不同气体而言，分子质量m越大，v_p值越小，而f(v)曲线峰值越大，从而曲线横向较窄。如图2.1-3所示。

图2.1-2

图2.1-3

(2)平均速率

平均速率即分子速度大小的算术平均值，其定义为

将速率分布函数f(v)代入并积分，得

注意:v₁～v₂速率间隔内分子的平均速率为－v'当v₁=0、v₂→∞时，上式分母

为1，则

(3)方均根速率

仿照平均速率的讨论可知，速率平方的平均值为

将速率分布函数f(　)v代入积分，开方后得方均根速率

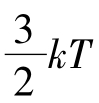三种速率中，最概然速率v_p用于速率分布的讨论;平均速率－用于平均碰撞频率和平均自由程的讨论;方均根速率用于平均平动动能的讨论，而且亦可由直接得出。

三种速率均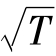与成正比，与成反比。三种速率的比例关系为

其中最大，v_p最小;常温下三种速率数量级约为每秒几百米，计算时尤其要注意采用SI单位制。由于三种速率有确定的比例关系，同一气体在确定温度下，知道一种速率，可求另外两种速率;另一情况是，在相同温度下

，知道一种气体的某种速率，可求另一气体的该种速率。

【例2.1-5】设图2.1-4所示的两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线，令(v_p)_O2和(v_p)_H2分别表示氧气和氢气的最概然速率，则正确结果是(　)。

(A)图中a表示氧气分子的速率分布曲线:(v_p)_O2/(v_p)_H2=4

(B)图中a表示氧气分子的速率分布曲线:

(v_p)_O2/(v_p)_H2=1/4

(C)图中b表示氧气分子的速率分布曲线:(

v_p)_O2/(v_p)_H2=1/4

(D)图中b表示氧气分子的速率分布曲线:(

v_p)_O2/(v_p)_H2=4

图2.1-4

解:最概然速率，对于摩尔质量，有μ_O2＞μ_H2。又因为温度T相同，所以有(v_p)_O2＜(v_p)_H2，故而曲线a为氧气，曲线b为氢气。正确答案为(B)。

【例2.1-6】某理想气体分子的平均速率－v若提高到原来的2倍，则该气体的温度T应提高到原来的(　)倍。

(A)2　(B)4　(C)8　(D)16

解:平均速率－v=，由题意2==4。正确答案为(B)。