动力学基本定律和质点运动微分方程

4.3.1　动力学基本定律和质点运动微分方程

1.动力学基本定律惯性坐标系

动力学基本定律，通称牛顿三定律。

(1)第一定律(惯性定律)

任何物体如不受外力作用，将保持静止或匀速直线运动。

(2)第二定律(力与加速度的关系定律)

质点受外力作用时，所产生的加速度与质点的质量有如下关系

(3)第三定律(作用与反作用定律)

两物体间相互作用的力同时存在，且等量、反向、共线。

第三定律在研究质点系动力学理论时有重要应用。

这些定律是古典力学的基础，它们不仅只适用于惯性坐标系，且只适用于研究速度远小于光速的宏观物体。由于一般工程问题中，大多数问题都属于上述适用范围，因此以基本定律为基础的古典力学在近代工程技术中仍占有很重要的地位。

2.质点运动微分方程

从动力学基本方程ΣF_i=ma可导出下列质点运动微分方程。

(1)矢量形式

(2)直角坐标形式

(3)自然坐标形式

一般地说，推导公式多用矢量形式，后两种形式多用于解具体问题。

质点运动微分方程求解以下两类问题。

①设已知质点的运动规律，求质点所受的力。用微分法一般不难求得解答。

②设已知作用于质点的力，求质点的运动规律。这归结为求解运动微分方程。一般地说，作用于质点的力可能是时间、质点的位置坐标、速度的函数;只有当函数关系较简单时，才能求得微分方程的精确解，如果函数关系复杂，则求解将相当困难，有时只能求出近似解。同时，求解微分方程时将出现积分常数，这些积分常数，须根据质点运动的初条件即初速度和初位置坐标来决定。所以，对这类问题，除了作用于质点的力(包括主动力、约束力)以外，还须知道质点运动的初条件，才能完全确定质点的运动。

【例4.3-1】图4.3-1(a)所示桥式起重机上的小车，吊着重为P=100kN的物体沿水平桥架以速度v₀=1m/s作匀速直线移动。重物的重心到悬挂点的距离为l=5m。当小车突然停车时，重物因惯性而继续运动，此后则绕悬挂点摆动。试求钢丝绳的最大拉力。

解:取重物为研究对象，并将重物视为质点。设小车突然停车后的任意瞬时t，钢丝绳与铅垂线的夹角为φ(φ角由图示铅垂轴x的正向逆时针转向取为正)。作用在重物上的力有:重物的重力P和钢丝绳的拉力T，受力图如图4.3-1(b)所示。取自然轴系的τ、n轴的正向如图4.3-1(b)所示(τ轴指向φ增加的一方)。由式4.3-4可得

显然，如能求出v(这是第二类问题)，则代入式(2)即可求得T。为此，将式(1)改写成为

图4.3-1

在初瞬时(即小车突然停车的瞬时)，重物的速度为v₀，钢丝绳与铅垂线的夹角为零，即t=0时v=v₀，φ=0;而在任一瞬时t时，重物的速度为v，钢丝绳与铅垂线的夹角为φ。作定积分得

式(3)就是重物的速度变化规律。当φ增大，v随之减小;当φ=0时，v²=v²₀，v值为最大。

由式(2)得

因为当φ=0时，v具有最大值v₀，cosφ=1也为最大值，故此时T具有最大值

图4.3-2

将v₀=1m/s，l=5m，P=100kN代入式(5)，可得

T_max=102kN

【例4.3-2】在地面以初速v₀铅直向上射出一物体(图4.3-2)。设地球引力与物体到地心的距离之平方成反比。求物体可能达到的最大高度。空气阻力不计。

解:以地面上发射物体处为坐标原点，x轴铅直向上。物体射出后，在运动过程中的任一位置，仅受到地球引力F，而

式中:G是引力常数;M_e是地球的质量;m是射出物体的质量;x是物体到

地面的距离。当物体在地面上时，即x=0，而F=mg，代入式(1)有mg=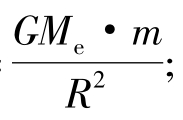因而GMe= gR²，F=于是物体的运动微分方程可写成

式中有三个变量t、v、x，需进行如下变换，以便积分。为此，将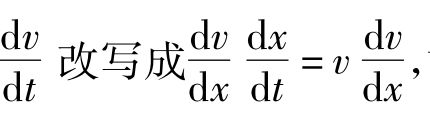故有

v从v₀到v，x从0到x，积分得

当物体到达最高点时，x=x_max，v=0，于是有

讨论:要使射出的物体脱离地球引力的影响，发射速度v₀应多大?从式(1)可见，要使物体不受地球引力作用，可令x=∞，而由式(2)则必须2gR－=0，即

这一速度称为第二宇宙速度。物体脱离地球后受到太阳引力而成为人造行星环绕太阳运动。