重力作用下流体静压强的分布规律

6.1.7　重力作用下流体静压强的分布规律

1.流体静力学基本方程

图6.1-5

在静止流体中取一底面积为dA、高为dz的竖直棱柱形隔离体，如图6.1-5所示。在重力作用下，水平方向因表面力大小相等，方向相反，互相抵消。在铅垂方向，作用在底面的压力为pdA，方向向上;顶面的压力为(p+dp)dA，方向向下;质量力只有重力，dG=ρgdAdz，方向向下。因隔离体在各力作用下平衡，故有

pdA－(p+dp)dA－ρgdAdz=0

化简上式得重力作用下流体静压强微分方程

对于不可压缩流体，ρ等于常数，积分上式得

将定解条件z=z₀时，p=p₀代入上式，求得积分常数C=p₀+ρgz₀。于是得流体静力学基本方程

式中:h=z₀－z为从液面算起的淹没深度;g为重力加速度，在流体力学中，一般取g=9.80m/s²。

从式6.1-14可知:①表面压强p₀将等值地传递到流体中的各点，这就是著名的压强传递的帕斯卡定律;②在重力作用下的静止均质流体中，液面下深度h相等各点的压强相等。压强相等各点组成的面称为等压面，故重力作用下的静止均质流体的等压面为水平面;③对于气体，因密度值较小(约为水的，当h不大时，任意两点的静压强可以认为是相等的。

通常建筑物表面和自由液面上都作用着当地大气压强p_a。当地大气压强值一般随海拔高度和气温变化。为便于计算，在工程技术中，常用一个工程大气压强(at)表示当地压强值。一个工程大气压相当于735mm汞柱或10m水柱对柱底产生的压强。我国法定计量单位中，压强的单位规定为N/m²或Pa，它们之间的换算关系为

1at=1kgf/cm²=98kN/m²=98kPa

2.绝对压强、相对压强、真空值

以绝对真空为零点计算的压强称为绝对压强，用p'表示;以当地大气压强p_a为零点计算的压强为相对压强，用p表示。在实际工程中，建筑物表面和自由液面多为大气压强p_a作用，故对建筑物起作用的压强仅为相对压强。

绝对压强和相对压强之间相差一个当地大气压强p_a，即

绝对压强p'总为正值，而相对压强p则可正可负。如果流体内某点的绝对压强小于当地大气压，其相对压强为负值，则称该点存在真空。真空的大小习惯以真空值

图6.1-6

或真空度表示。真空值p_v总为正值。

绝对压强、相对压强和真空值三者的关系如图6.1-6所示。

【例6.1-1】图6.1-7所示封闭容器的水面绝对压强p'0=85kPa，中央玻璃管两端开口，试求玻璃管应伸入水面以下若干深度时，既无空气通过玻璃管进入容器，又无水进入玻璃管。

解:将式6.1-14用于玻璃管底部一点，有

图6.1-7

为避免出错，计算时应注意式中各项单位的统一。

【例6.1-2】已知安装在图6.1-8所示封闭水箱上的金属测压计读值p_表=4900Pa，金属测压计中心、液面分别比A点高h₁=0.5m和h₂=1.5m，试求液面的相对压强和绝对压强。

图6.1-8

解:将式6.1-14用于A点，有

p_A=p_表+ρgh₁=p₀+ρgh₂

则液面的相对压强为

由于p₀＜0，说明液面存在真空，其真空值为

p_v=p_a－p'=－p₀=4900Pa

液面的绝对压强为

p'0=p₀+p_a=－4900+98000=93100Pa

注意:金属测压计读值为相对压强值，为什么?请读者思考。

3.流体静压强分布图

实际工程中，常用流体静压强分布图来分析问题和进行计算。绘制流体静压强分布图所用知识点有流体静力学基本方程和流体静压强的两个特性。因p与h呈线性关系，故只需任取两对(p，h)，连成一直线，即可绘出。图6.1-9为几种壁面上的相对压强分布图，其中矢线的长短表示压强的大小，箭头方向即为压强的方向，垂直于受压面。

4.位置水头、压强水头、测压管水头

由式6.1-13可得流体静力学基本方程的另一形式

上式说明，在连续均质的静止流体中，各点的z+等于常数。

现说明式6.1-17各项的几何意义。如图6.1-10所示盛水封闭容器，若在容器壁上任意点接上开口玻璃管(称为测压管)，则测压管内液面离基准面的高度系由位置高度z和压强高度两部分组成。在流体力学中，通常用“水头”代表高度，故z称为位置水头称为压强水头(也称为测压管高度)，而z+则称为测压管水头。在均质连续的静止流体中，各点的测压管水头保持不变。

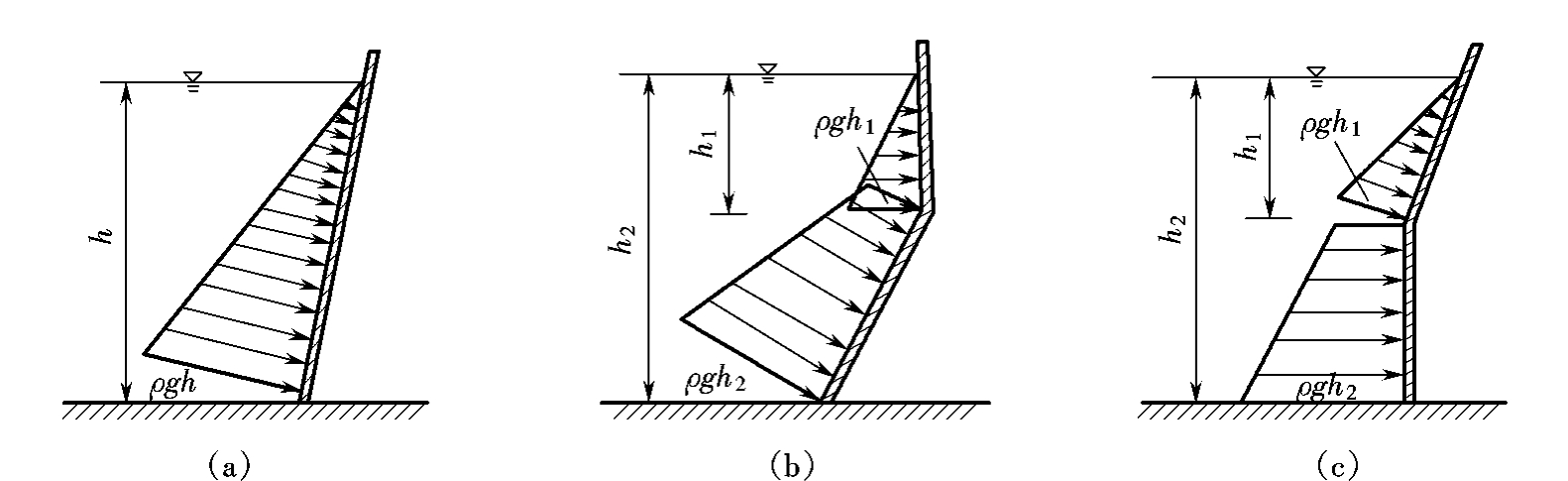
图6.1-9

图6.1-10