静止液体作用在平面上的总压力

6.1.8　静止液体作用在平面上的总压力

静止液体作用在平面上的总压力的大小、方向和作用点的确定，是许多工程设计必须解决的流体力学问题。

1.总压力的大小

设在静止液体中有一与水平面交角为α、面积为A的平面ab，如图6.1-11所示，平面ab左侧承受液体压力，右侧及液面均作用着大气压强p_a。为分析方便，将平面ab绕Oy轴旋转90°，建立图示xOy坐标系。

在平面ab上任取一微小面积dA，其中心位于液面以下的深度为h，则作用在微小面积上的液体总压力为dP=ρghdA=ρgysinαdA，因作用在平面ab各微小面积上的dP方向相同，根据平行力系求和原理，将dP沿受压面积分，可得作用在受压面上的总压力

图6.1-11

式中∫_AydA为受压面积对x轴的静矩，据理论力学知，它等于受压面积A与其形心坐标y_C的乘积。因此

式中h_C、p_C分别为受压曲面形心处的淹深和相对压强。

2.总压力的方向

总压力P的方向，与dP方向相同，即沿受压面内法线方向。

3.总压力的作用点

总压力P的作用点(也称压力中心)位置，可用理论力学中的合力矩定理求得。对x轴有

将P=ρgsinα·y_CA和dP=ρgysinαdA代入，化简得

式中∫_Ay²dA=I_x为受压面对x轴的惯性矩，为使用上的方便，可根据惯性矩平行移轴公式I_x= I_C+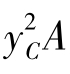将其换算成受压面对通过其形心C且平行于x轴的轴线的惯性矩I_C，于是得压力中心基本公式

因恒大于零，故y_D＞y_C，即压力中心D总是在受压面形心C的下方。注意，应用式6.1-19时，坐标原点必须放在自由液面上。

【例6.1-3】图6.1-12所示为一宽b、高h的铅直矩形平板闸门，试求作用在闸门上的静水总压力和作用点位置，并说明图算法原理。

解:总压力由式6.1-18得

式中A_P=为压强分布图面积。由此可见，静止液体作用在矩形平面上的总压力恰等于以压强分布图面积为底、以平面宽度为高的体积。

作用点位置由式6.1-19得

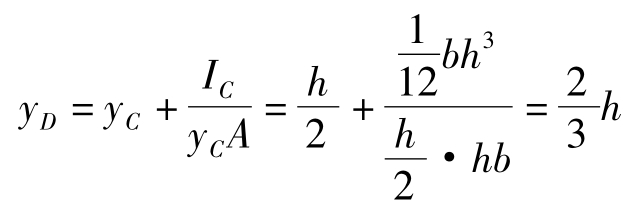
图6.1-12

恰位于通过压强分布图体积形心引出的合力作用线与受压面的交点。

图6.1-13

图算法仅适用于受压面为矩形的情况。

【例6.1-4】图6.1-13为绕铰链O转动的自动开启式矩形闸门，倾角α=60°，要求h₁=2.0m、h₂=0.4m时，闸门自动开启。试求铰链至水闸下端的距离x。

解:确定闸门承受的静水总压力及作用定位置。设闸门宽度为b，则

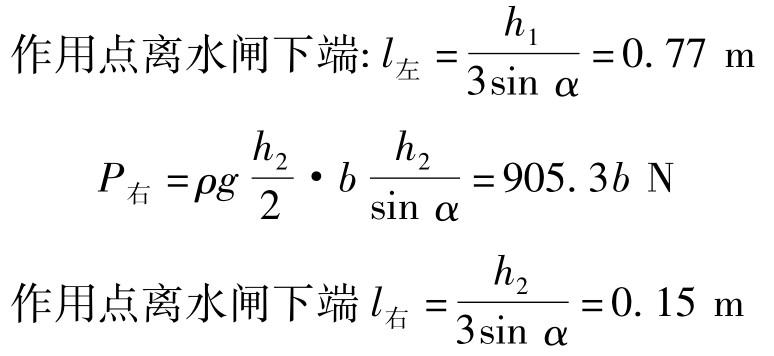
要使闸门自动开启，则必有

P_左(x－l_左)≤P_右(x－l_右)

将P_左、l_左、P_右、l_右代入上式，得x≤0.8m。

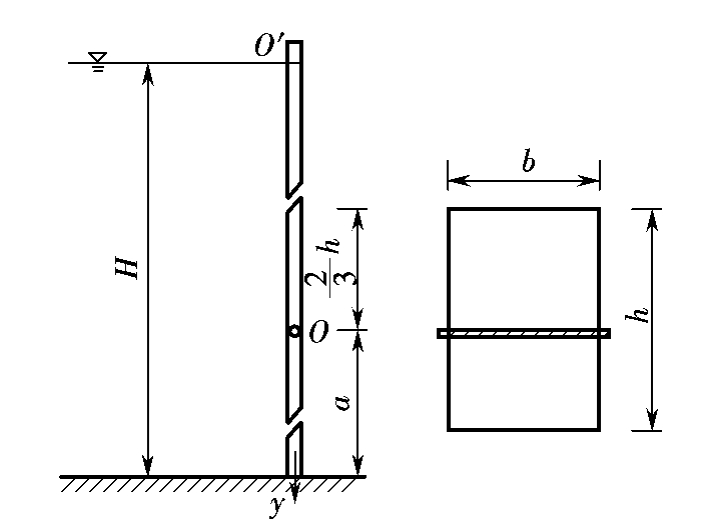
图6.1-14

【例6.1-5】如图6.1-14所示矩形闸门，已知a及h，试求H为多少时，闸门可绕转轴O自动打开。

解:本题解法有多种，下面介绍一种较为简单的解法。要使闸门自动打开，则必有

即作用在闸门上的静水总压力的作用点必须位于转轴

上方。将y_C=H^－a－bh³，A=bh代入上式，化简即得