圆管中的紊流运动

6.3.4　圆管中的紊流运动

1.紊流运动的特征

严格地讲，紊流总是非恒定流。但引入时间平均流动概念后，只要某运动要素的时间平均值不随时间变化就可视为恒定流。前面根据恒定流导出的流体动力学基本方程，对于时间恒定紊流仍可照常适用。

2.紊流切应力

紊流中的切应力τ除了由黏性引起的切应力τ₁外，还存在由紊动产生的附加切应力τ₂，即

式中:τ₁=μ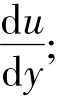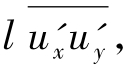经分析τ₂=－普朗特设想流体质点的紊流运动与气体分子运动类似，提出半经验的混合长度理论，推导出

这里l称为混合长度，但没有直接的物理意义。

式(6.3-14)中两部分切应力的大小随流动情况有所不同。当雷诺数较小时，脉动较弱，τ₁占优。随着雷诺数增加，脉动加剧，τ₂逐渐加大，至雷诺数相当大时，τ₁甚至可以忽略不计。

3.紊流流速分布

紊流的流速分布在紧贴固壁附近和紊流核心区是不同的。在紧贴固壁附近有一极薄流层，由于流动受边壁限制，消除了流体质点的掺混，时均流速为线性分布，切应力中τ₂可忽略不计，就其时均特征来说，这一薄层可认为属于层流运动，故称为层流底层或黏性底层。黏性底层之外的流区，称为紊流核心，在紊流核心区内，由于流体质点相互掺混和动量变换，使过流断面上流速趋于均化。根据普朗特混合长度理论可得紊流过流断面上流速

为对数分布规律。式中v_x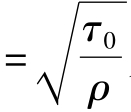为剪切速度;k为卡门通用常数，可由实验确定;y为从管壁起算的径向距离;C为常数，取决于边界条件。

4.沿程水头损失

紊流的沿程水头损失计算公式仍为达西公式(6.3-13)。一般情况下，式中沿程阻力系数λ=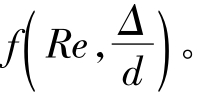紊流的λ无法像圆管层流一样由理论推导得到，只能依靠实验研究。为了探讨λ与Re和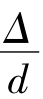的变化规律，德国科学家尼古拉兹在实验室对人工粗糙管(即在管壁上人为均匀地粘上一定粒径的砂子的管道)进行大量的实验，其结果如图6.3-4所示，称为尼古拉兹实验曲线图。

根据λ的变化特征，图中曲线可分为五个区域，即

层流区(ab线):Re＜2300，λ=f(Re)=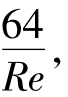管流的沿程水头损失h_f∝v^1.0，与理论分析成果完全一致。

层流向紊流的过渡区(bc线):2300＜Re＜4000，λ=f(Re)，与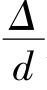无关。

图6.3-4

紊流光滑区(cd线):4000＜Re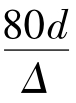＜，此区内由于粗糙度Δ被黏性底层所覆盖，对沿程阻力系数λ没有影响，λ=f(Re)，h_f∝v^1.75。

紊流过渡区(cd线和ef线之间的区域):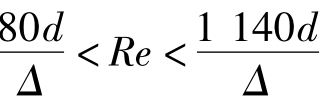，随着Re的增大，黏性底层厚度减小，粗糙度Δ开始发生影响。在该区λ与Re和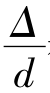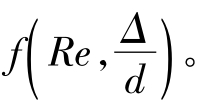都有关系，即λ=

紊流粗糙区(ef线以右的区域):Re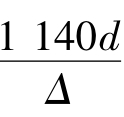＞，曲线呈水平线，λ与Re无关，而仅与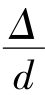有关，即λ=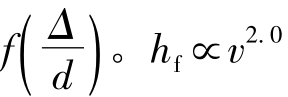，故该区亦称为阻力平方区。

尼古拉兹实验使用的人工粗糙管，其成果不能完全用于工业管道。原因在于工业管道的粗糙物是在制造过程中形成的，其粗糙物在形状、大小、分布规律等方面与人工粗糙管有很大差异。柯列勃洛克根据大量工业管道试验资料，提出了适用于工业管道紊流三个区的λ计算公式，即柯列勃洛克公式

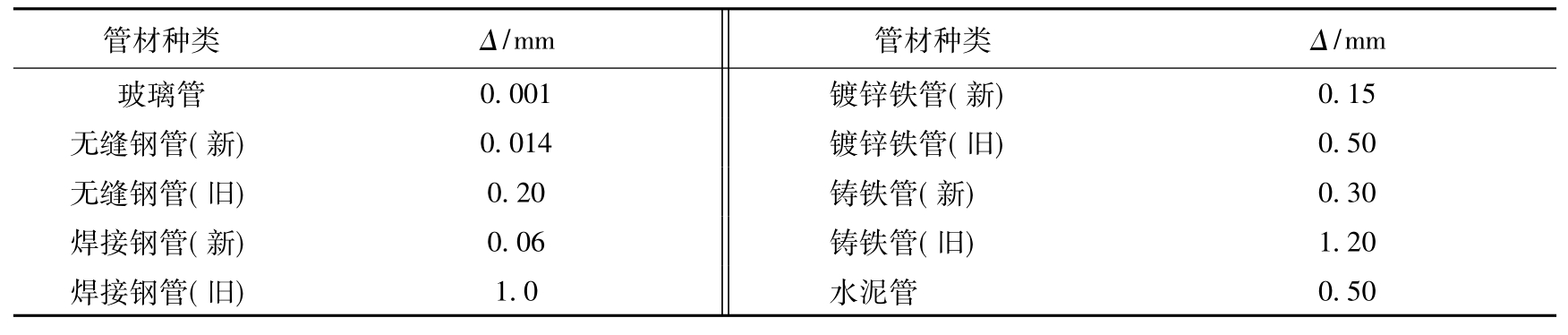
上式在工业管流的计算中应用广泛。式中Δ为工业管道的当量粗糙高度。常用管材的当量粗糙度见表6.3-1。

表6.3-1　常用管材的当量粗糙度Δ

式(6.3-17)比较复杂，计算很不方便。下面两个公式计算较为简便，同样适用于工业管道的紊流三个区。

对于明渠水流，通常采用谢才公式

其中谢才系数

表明C和λ一样是反映沿程阻力系数变化规律的系数。在紊流粗糙区，谢才系数可直接由下列经验公式计算。

式中:R为水力半径，以m计;n为渠壁粗糙系数，亦称糙率，为综合反映壁面粗糙情况的无量纲数，见表6.3-2。

表6.3-2　粗糙系数n值

【例6.3-3】已知城市给水干管某处的水压p=196.2kPa，从该处引出一根水平输水管，直径d=250mm，当量粗糙高度Δ=0.4mm。若要保证通过流量Q=50L/s，问能输送到多远(水的运动黏度ν=0.0131cm²/s)?

解:由干、支管相接处至支管出口建立柏努利方程，有

即能输送4100m远。