交流电路功率及功率因数

7.2.13　交流电路功率及功率因数

1.交流电路功率

从电路的功能关系看，正弦交流电路包括以下三个功率的计算。

①视在功率S是电源供出的总电压和总电流的有效值的乘积，

它表示负载工作时所占用的电源容量，单位为“VA”。

②有功功率P是负载消耗的电能量，它的计算式为

这部分能量转变为电路对外部所做的有用功，单位为“W”。

③无功功率Q用于负载与电源之间的能量交换，

该功率并不转换为有用功，但要占用电源的容量，单位为“Var”。

三个功率构成直角三角形，称为功率三角形，如图7.2-34，三者满足关系式

④功率与RLC各元件功率的关系。

对于电阻元件，只消电能量，不存在与电源间的能量交互，所以

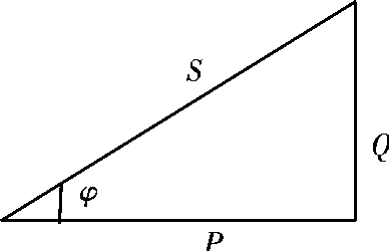
图7.2-34　功率三角形

对于电感元件，不断地吸收电能量和放出磁场能，它和电源之间只形成等量的能量交换，并不消耗能量，所以

对于电容元件，不断地和电源之间只形成等量的能量交换，不消耗能量，所以

电路的总有功功率(平均功率)等于RLC各元件功率有功功率之和，即

电路的总无功功率等于

2.功率因数

式(7.2-31)中的“cosφ”称为交流电路的功率因数。它表示交流电路中实际消耗的有用功在整个电源容量中所占的比例，代表了交流电路中电能有效利用的程度。功率因数cosφ的计算式如下:

式中的φ为阻抗角，功率因数cosφ还可根据式(7.2-29)计算，即

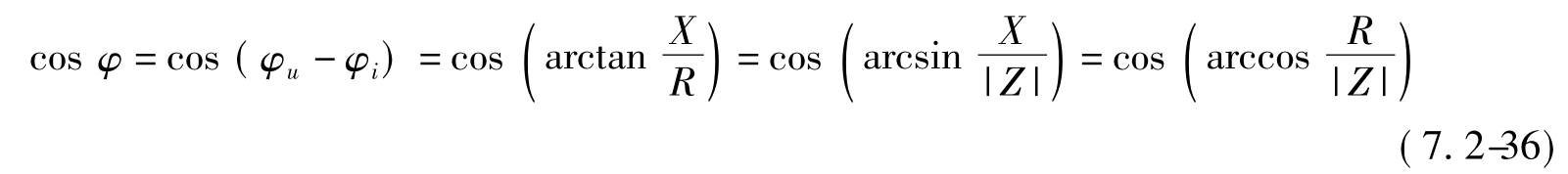
由此不难看出，功率因数cosφ是由电路参数所决定的固有性质。

3.提高功率因数及过补偿问题

对于力能电路而言，不允许低效率的电路(低功率因数的交流电路)存在，因此当电路的功率因数较低时，需要通过调整电路的参数来提高它的功率因数。由于力能电路中的电感性质的负荷比重很大，因此，提高功率因数的有效办法之一是在感性负载两端并联一个适当的电容，如图7.2-35所示。

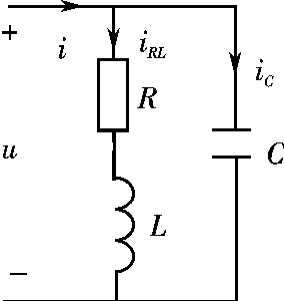
图7.2-35　提高功率因数措施

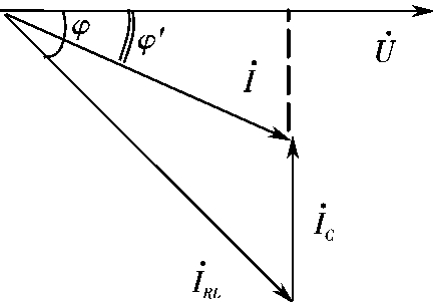
图7.2-36　图7.2-35的相量图

图7.2-35的相量图如图7.2-36。设电路外加电压初相位为0，由于感性负载的端电压u超前流过的电流i_RL，所以电流相量位于第四象限;又因为“电容电流超前电容电压90°”和6I=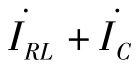，得到电流i相量。由此图容易看出，感性负载并联电容后，电路电压与电流间的相位差从φ变到了φ'，因为φ'＜φ，所以cosφ'＞cosφ，功率因数得到了提高。功率因数一旦得到提高，电源的利用率以及电路的传输率也随之得到提高。

当外加电源电压一定时，电容值越大，电容电流则越大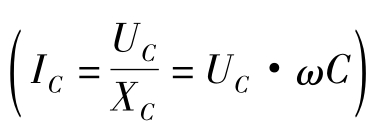，这会使φ'随电容的增大逐渐变小，φ'过0后，如果继续增大电容，会因电流I_C继续增大，使φ'从0逐渐变负(绝对值变大)，此后电容值越大，功率因数反而下降，称为过补偿。应避免过补偿。

【例7.2-9】如图7.2-37(a)电路中，电容C可调，若感性负载的功率因数为cosφ，并接电容后，电路的功率因数为cosφ'，电路的端口电流i的有效值I和电容C的关系如图7.2-37(b)所示，则下列说法不正确的是(　)。

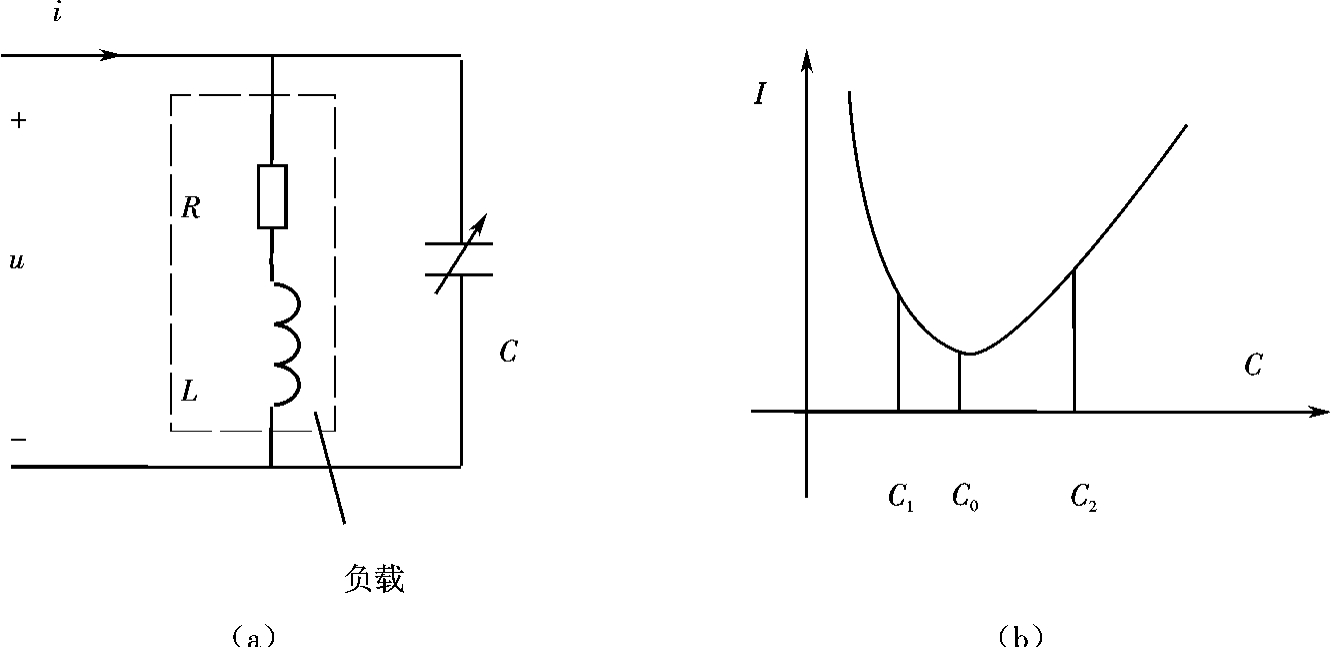
图7.2-37　例7.2-9图

(A)当C=C₀时，电路的功率因数最大

(B)当C＜C₀时，cosφ'＞cosφ

(C)当电路出现过补偿时，C＞C₀

(D)当C＞C₀时，cosφ'＞cosφ

解:答案为(D)。

当外加电源电压一定时，电容值越大，电容电流则越大，当C=C₀时，电流最小，φ'=0，cosφ'=1，电路效率最高，如果继续增大电容，使C＞C₀，会因电流I_C继续增大，使φ'的绝对值变大，此后电容值越大，功率因数反而下降，出现过补偿现象，应避免过补偿。因此选项(A)、选项(B)及选项(C)的说法都是正确的。