变压器的电路模型如图7.3-1所示。
设变压器的一次绕组的匝数为N1,二次绕组的匝数为N2,则
![]()
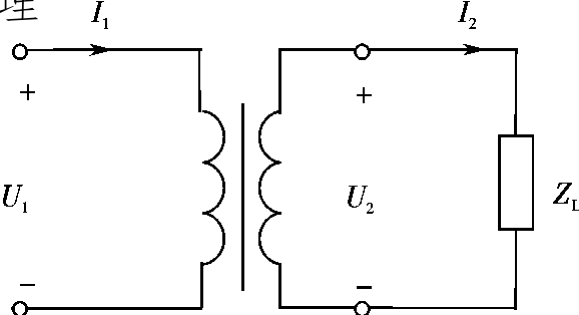
图7.3-1 变压器电路
称k为变压器的变比。变压器的变比决定了变压器的电压变换、电流变换以及阻抗变换能力。
1.电压变换
![]()
该式说明:电源端电压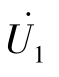 通过变比为k的变压器将
通过变比为k的变压器将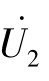 送入负载ZL。
送入负载ZL。
2.电流变换
U1I1=U2I2
根据式(7.3-1)得
![]()
3.阻抗变换
将变压器和变压器的负载整体看作一个二端网络,该二端网络的等效阻抗设为Z*LZ,如图7.3-2所示。利用变压器的电压变换式(7.3-1)和电流变换式(7.3-2)可以推出ZL与Z*L大小之间的关系式(7.3-3):
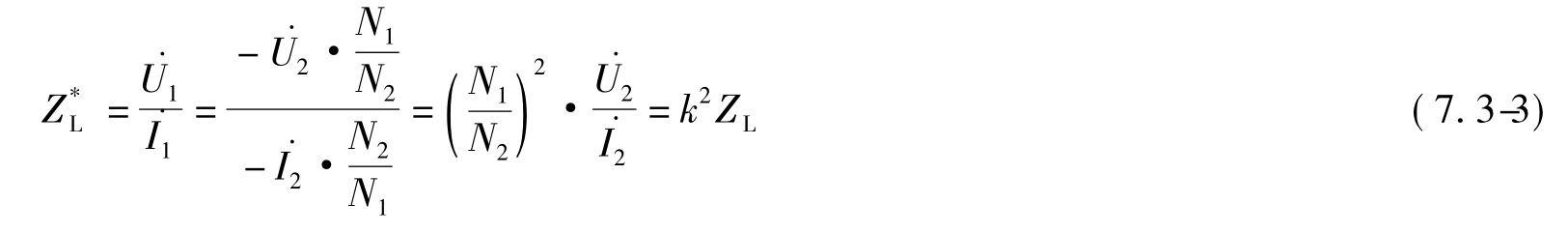
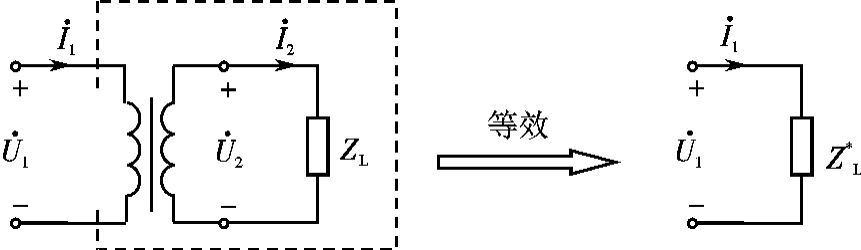
图7.3-2 变压器的阻抗变换
利用阻抗匹配可以使电路的电源输出最大功率,或者说使电源的负载获得最大功率。
例如:一个正弦信号源的电压US=50V,RS=1000W,负载电阻40Ω,0.8W。若电源与负载直接相连,如图7.3-3(a),则

图7.3-3 变压器的阻抗匹配作用
![]()
负载消耗功率:P=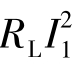 =0.0925W。也就是说,负载仅能从电源获得0.0925W的电能量。若电源通过变压器与负载相连,如图7.3-3(b),则根据理想变压器的特点(P1=P2),并利用阻抗变换表达式(
=0.0925W。也就是说,负载仅能从电源获得0.0925W的电能量。若电源通过变压器与负载相连,如图7.3-3(b),则根据理想变压器的特点(P1=P2),并利用阻抗变换表达式(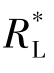 =k2RL),可得负载的消耗功率为
=k2RL),可得负载的消耗功率为
![]()
当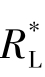 =RS时,
=RS时,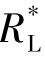 可从电源处获得最大的功率,也就是RL从电源处获得最大的功率,所以当变压器变比k=
可从电源处获得最大的功率,也就是RL从电源处获得最大的功率,所以当变压器变比k=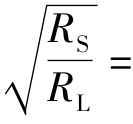 5时,负载RL可获得的最大功率,即Pmax=0.625W。
5时,负载RL可获得的最大功率,即Pmax=0.625W。
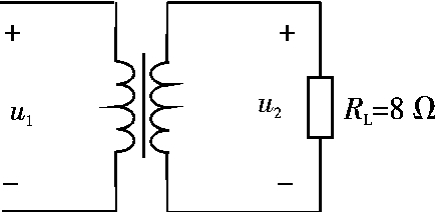
图7.3-4 例7.3-1图
【例7.3-1】在图示7.3-4电路中,负载RL的消耗功率为72 W,若变压器的变压比k=5,则变压器原边电压有效值U1( )。
(A)等于120V (B)等于4.8V
(C)等于0.6V (D)无法计算
解:根据负载的消耗功率和电阻值,可得付边电压有效值U2: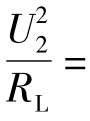 P=72W,U2=24V。根据变压器的电压变比k
P=72W,U2=24V。根据变压器的电压变比k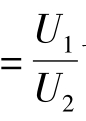 可得:U1=120V,所以,选项(A)正确。(B)选项错误地认为U1=kU2。
可得:U1=120V,所以,选项(A)正确。(B)选项错误地认为U1=kU2。
【例7.3-2】如图7.3-5所示理想变压器,试确定输出电阻RL获得最大功率时的匝数比。
解:首先对变压器一次绕组左侧的有源二端网络进行戴维南等效,即用一个电压源模型等效代替,其内阻RS=R1//R2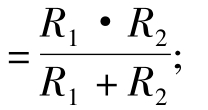
然后利用阻抗变换将变换至一次绕组侧,即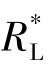 =k2RL,等效电路如图所示。
=k2RL,等效电路如图所示。
最后根据最大功率原理知: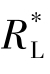 =RS时,
=RS时,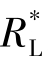 获得最大功率,即RL获得最大功率,由此得匝数比k=
获得最大功率,即RL获得最大功率,由此得匝数比k=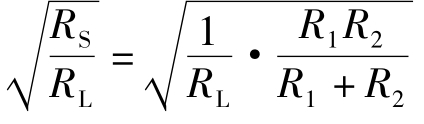
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















