有效数字和数值的修约及其运算

第一节　有效数字和数值的修约及其运算

一、概念

有效数字系指在检验工作中所能得到的有实际意义的数值，其最后一位数字欠准是允许的，这种由可靠数字和最后一位不确定数字组成的数值，即为有效数字。

最后一位数字的欠准程度通常只能是上下差1个单位。

有效数字的定位（数位）是指确定欠准数字的位置。这个位置确定后，其后面的数字均为无效数字。欠准数字的位置可以是十进位的任何数位，用10ⁿ来表示：n可以是正整数，如n＝1，即10¹＝10（十数位）；n＝2，即10²＝100（百数位）……。n也可以是负整数，如n＝－1，即10^－1＝0.1（十分位）；n＝－2，即10^－2＝0.01（百分位）……

二、检验中的有效数字

在没有小数位且以若干个零结尾的数值中，有效位数系指从非零数字最左一位向右数得到的位数减去无效零（即仅为定位用的零）的个数。例如，35000中若有2个无效零，则为3位有效位数，应写作350×10²；若有3个无效零，则为2位有效位数，应写作35×10³。

在其他十进位数中，有效数字系指从非零数字最左一位向右数而得到的位数。例如3.2、0.32、0.032和0.0032均为2位有效数字，0.320为3位有效位数，10.00为4位有效位数，12.490为5位有效位数。

非连续型数值（如个数、分数、倍数）是没有欠准数字的，其有效位数可视为无限多位。例如，分子式H₂SO₄中的“2”和“4”是个数。常数π、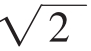等数值的有效位数也可视为无限多位；含量测定项下的“0.3g”或“1ml：25mg”中的“0.3”“1”和“25”为标示量，其有效位数也均为无限多位。即在计算中，其有效位数应根据其他数值的最少有效位数而定。

pH值等对数值，其有效位数是由其小数点后的位数决定的，其整数部分只表明其真数的乘方次数。如pH＝11.26（［H^＋］＝5.5×10^－12mol/L），其有效位数只有两位。

有效数字的首位数字为8或9时，其有效位数可以多记一位。例如，85％与115％，都可以看成是3位有效数字；99.0％与101.0％都可以看成是3位有效数字。

三、数值修约及其进舍规则

1.数值修约

是指对拟修约数值中超出需要保留位数时的舍弃，根据舍弃数来保留最后一位数或最后几位数。

2.修约间隔

是确定修约保留位数的一种方式，修约间隔的数值一经确定，修约值即应为该数值的整数倍。例如，制订修约间隔为0.1，修约值即应在0.1的整数倍中选取，也就是说，将数值修约到小数点后1位。

3.确定修约位数的表达方式

制订修约间隔为10^－n（n为正整数），或指明将数值修约到小数点后n位。

指定修约间隔为1，或指明将数值修约到个数位。

指定修约间隔为10ⁿ（n为正整数），或指明将数值修约到10ⁿ数位，或指明将数值修约到“十”“百”“千”……数位。

指定将数值修约成n位有效位数（n为正整数）。

4.进舍规则

拟舍弃数字的最左一位数字小于5时，则舍去，即保留的各位数字不变。

【例1】将12.1498修约到一位小数（十分位），得12.1。

【例2】将12.1498修约成两位有效位数，得12。

拟舍弃数字的最左一位数字为5，而右面无数字或皆为0时，若所保留的末位数为奇数（1，3，5，7，9），则进1；为偶数（2，4，6，8，0），则舍弃。

【例1】修约间隔为0.1（或10^－1）。

拟修约数值　　　　　　　　　修约值

1.050　　　　　　　　　　　　1.0

0.350　　　　　　　　　　　　0.4

【例2】修约间隔为1000（或10³）。

拟修约数值　　　　　　　　　修约值

2500　　　　　　　　　　　　2×10³

3500　　　　　　　　　　　　4×10³

【例3】将下列数字修约成2位有效位数。

拟修约数值　　　　　　　　　修约值

0.0325　　　　　　　　　　　0.032

32500　　　　　　　　　　　 32×10³

5.不许连续修约

修约数字应在确定修约位数后一次修约获得结果，而不得多次按前面规则连续修约。

【例1】修约15.4546，修约间隔为1。

正确的做法为：15.4546→15

不正确的做法为：15.4546→15.455→15.46→15.5→16

为便于记忆，上述进舍规则可归纳成下列口诀：四舍六入五考虑，五后非零则进一，五后全零看五前，五前偶舍奇进一，不论数字多少位，都要一次修约成。

四、运算规则

在进行数学运算时，对加减法和乘除法中有效数字的处理是不同的：

许多数值相加减时，所得和或差的绝对误差必较任何一个数值的绝对误差大。因此相加减时应以诸数值中绝对误差最大（即欠准数字的数位最大）的数值为准，以确定其他数值在运算中保留的数位和决定计算结果的有效位数。

许多数值相乘除时，所得积或商的相对误差必较任何一个数值的相对误差大。因此相乘除时应以诸数值中相对误差最大（即有效位数最少）的数值为准，确定其他数值在运算中保留的位数和决定计算结果的有效位数。

在运算过程中，为减少舍入误差，其他数值的修约可以暂时多保留一位，等运算得到结果时，再根据有效位数弃去多余的数字。

【例1】13.65＋0.00823＋1.633＝？

本例是数值相加减，在3个数值中13.65的绝对误差最大，其最末一位数为百分位（小数点后2位）。因此将其他各数均暂先保留至千分位，即把0.00823修约成0.008，1.633不变，进行运算：

13.65＋0.008＋1.633＝15.291

最后对计算结果进行修约，15.291应只保留至百分位，而修约成15.29。

【例2】14.131×0.07654÷0.78＝？

本例是数值相乘除，在3个数值中，0.78的有效位数最少，仅为两位有效位数。因此各数值均应暂保留3位有效位数进行运算，最后结果再修约为2位有效位数。

14.131×0.07654÷0.78

＝14.1×0.0765÷0.78

＝1.08÷0.78

＝1.38

＝1.4

【例3】计算恩诺沙星（C₁₉H₂₂FN₃O₃）的分子量。

在诸元素的乘积中，原子数的有效位数可视作无限多位，因而可根据各原子量的有效位数对乘积进行定位，而在各乘积的相加中，由于分子量的数值保留到小数点后2位（百分位），因而应将各元素的乘积修约到千分位（小数点后3位）后进行相加；再将计算结果修约到百分位，即得。

12.011×19＋1.00794×22＋18.9984032＋14.006747×3＋15.9994×3

＝228.209＋22.17468＋18.9984032＋42.020241＋47.9982

＝228.209＋22.175＋18.998＋42.020＋47.998

＝359.400

＝359.40

五、注意事项

正确记录检验所得的数值应根据取样量、量具的精度、检测方法的允许误差和标准中的限度规定，确定数字的有效位数（或数位），检检值必须与测量的准确度相符合，记录全部准确数字和一位欠准数字。

正确掌握和运用规则不论用何种办法进行计算，都必须执行进舍规则和运算规则，如用计算器进行计算，也应将计算结果经修约后再记录下来。

要根据取样的要求，选择相应的量具。

“精密称定”系指称取重量应准确到所取重量的0.1％，可根据称量选用分析天平或半微量分析天平；“精密量取”应选用符合国家标准的移液管；必须时应加校正值。

“称定”（或“量取”）系指称取得重量（或量取的容量）应准确至所取重量（或容量）的百分之一。

取用量为“约xx”时，系指取用量不得超过规定量的100±10％。

取用量的精度未作特殊规定时，应根据其数值的有小数位选用与之相应的量具；如规定量取5ml或5.00ml时，则应分别选用5～10ml的量筒、5～10ml的刻度吸管或5ml的移液管进行量取。

在判定药品质量是否符合规定之前，应将全部数据根据有效数字和数值修约规则进行运算，将计算结果修约到标准中所规定的有效位，而后进行判定。

【例1】异戊巴比妥钠的干燥失重，规定不得超过4.0％，今取样1.0042g，干燥后减失重量0.0408g，请判定是否符合规定？

本例为3个数值相乘除，其中0.0408的有效位数最少，为3位有效数字，以此为准。（在运算过程中暂时多保留一位）

0.0408÷1.004×100.0％＝4.064％

因异戊巴比妥钠规定的限度为不得超过4.0％，故将计算结果4.064％修约到千分位为4.1％，大于4.0％应判为不符合规定（不得大于4.0％）。

如将上述规定的限度改为“不得大于4.0％”，而其原始数据不变，则将计算结果修约至百分位，得4％，未超过4％的限度，应判为符合规定（不得大于4.0％）。