检验与优化分析

2.2.2　作物水肥耦合模型的建立、检验与优化分析

2.2.2.1　作物水肥耦合模型的建立^④

2.2.2.1.1　试验处理设计

以三因素二次回归通用旋转组合设计方法为例。根据农业生产实际状况和群众经验，确定影响作物产量的因素z₁、z₂、z₃及其上、下限，其中z₁的上、下限为z₂₁、z₁₁，z₂的上、下限为z₂₂、z₁₂，z₃的上、下限为z₂₃、z₁₃，各因素的零水平(z_pj)和变化间隔(Δ_j)分别为：

z_pj=(z_1j+z_2j)/2　　　　　(2-2-1)

Δ_j=(z_2j-z_pj)/γ　　　　　(2-2-2)

式中：z_1j——因素的下限;

　z_2j——因素的上限;

　j——因素个数，j=1，2，3;

　γ——星号臂，根据二次回归通用旋转性的要求确定，即γ=2^m/4=1.682。

对因素各水平(z_j)取值作线性变换：

x_j=(z_j-z_pj)/Δ_j　　　　　(2-2-3)

则有因素水平编码表，见表2-2-1。

根据回归通用旋转组合设计(即在因子空间中选择几个具有不同半径的球面上的点，把它们适当组合起来而形成试验计划)的要求，则试验处理数(n)为：

n=m_c+m_γ+m₀=2³+2×⒏3+6=20　　(2-2-4)

式中：m_c——分布在半径为ρ_c=m^1/2的球面上的点，即以二水平(+1和-1)为基础的全因素试验的试验处理数，亦即m_c=2^m(m为因素数);

表2-2-1　因素水平编码

m_γ——分布在半径为ρ_γ=γ的球面上且在m个坐标轴上的星号点，即每个因素的坐标轴上各两个以原点为中心的对称点，亦即m_γ=2m;

m₀——集中在半径为ρ₀=0的球面上的点，即在各变量都取零水平的中心点的重复试验次数。m₀的选取应使二次旋转组合设计具有“几乎正交性”，即除常数项b₀和二次项系数b_jj之间尚有相关外，其他回归系数间都不存在相关。

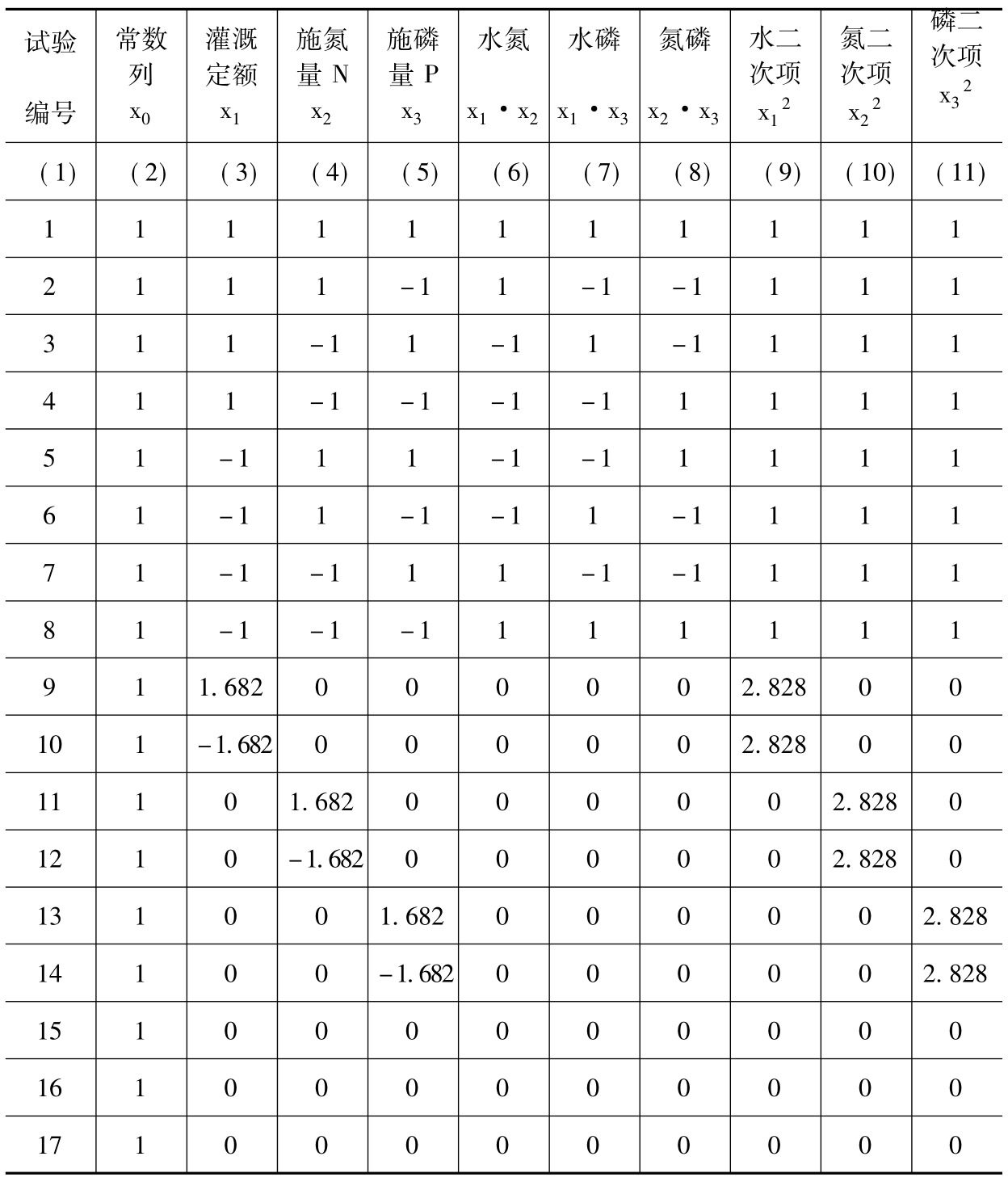
于是得三因素二次回归通用旋转组合设计结构矩阵(X)如表2-2-2中(2)～(11)列，其中试验方案由表2-2-2中第(3)、(4)、(5)列组成。

2.2.2.1.2　田间实施

试验处理在田间随机排列或顺序排列，各处理采用合适的灌溉技术进行灌溉，按要求施入肥料。观测有关作物生育阶段、作物生育性状、灌水前后和各生育阶段分界点的土壤水分及有关气象数据。

2.2.2.1.3　作物水肥耦合模型的建立

作物水肥耦合模型一般可以用二次回归旋转模型表示，即

式中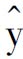：——表示回归估计值;

　x_j——表示线性变换后的无因次变量;

　b_j——表示回归模型的一次项系数;

　b_ij——表示回归模型的交互项系数;

　b_jj——表示回归模型的二次项系数;

　m——表示因素数;

　j——表示因素的序号。

回归系数的计算方法如下：

设Y=(y₁，y₂...y_n)^T是二次回归通用旋转组合设计的试验结果，X是其结构矩阵［见表2-2-2中(2)～(11)列中的系数矩阵］，则X的转置矩阵X'及信息矩阵A均可得出。下面列出A矩阵：

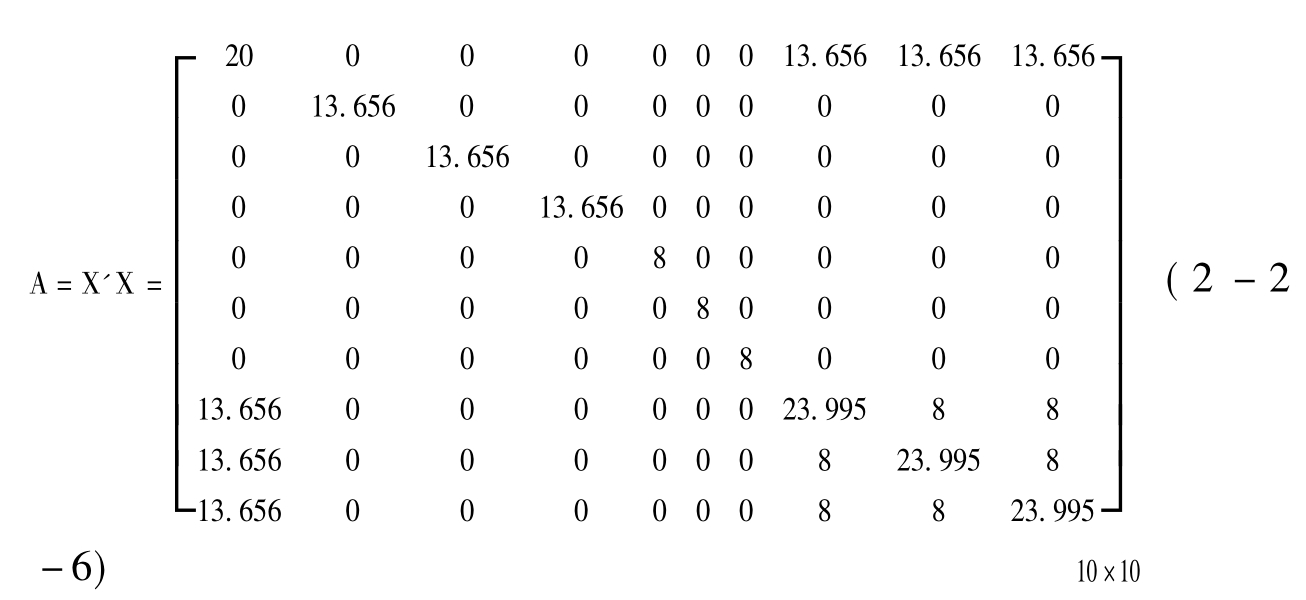
其常数矩阵为：

B=X'·Y=［B₀，B₁，B₂，B₃，B₁₂，B₁₃，B₂₃，B₁₁，B₂₂，B₃₃］^T　　　(2-2-7)

式中　B₀=∑y_L;

　　　B_j=∑x_Ljy_L　　(j=1，2，...，m)

(为方便起见，记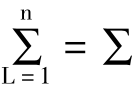，其中L为试验处理数编号，下同)

B_ij=∑x_Lix_Ljy_L　［i=1，2，3，...(m-1);j=1，2，...m;i＜j］

其回归系数矩阵b为：

b=C·B　　　　　(2-2-8)

式中：C——为相关矩阵，C=A^-1，由矩阵A经初等变换、分块、求逆，可得出逆矩阵A^-1。

于是(2-2-8)式可转化为：

式(2-2-9)中逆矩阵A^-1中的元素a₁、a₂、a₃、a₄、a₅、a₆的值如下：

a₁=0.16634　　a₂=-0.05679　　a₃=0.07322

a₄=0.12500　　a₅=0.00689　　 a₆=0.06939

在旋转设计下，若相关矩阵C取回归正交组合设计的形式，则b矩阵由上述三个因素可以推广到m个因素，其回归系数通式为：

b_j=a₃∑x_Ljy_L

b_ij=a₄∑x_Lix_Ljy_L　　(i＜j)　　　　　(2-2-10)

表2-2-2　三因素二次通用旋转组合设计结构矩阵(X)及产量结果

根据产量结果，编制FORTRAN程序上机计算，可求得作物水肥耦合回归模型(2-2-5)式。

2.2.2.2　作物水肥耦合模型的检验

2.2.2.2.1　作物水肥耦合回归方程的显著性检验^②

1.采用统计量F₂对回归方程进行显著性检验

式中：D_回=D_总-D_剩

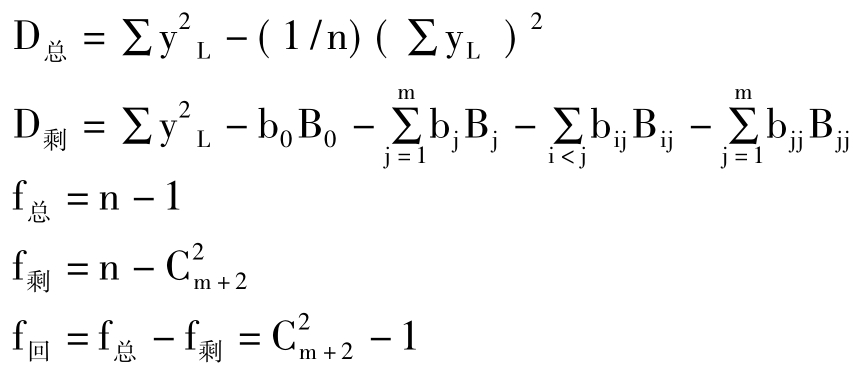
　D_回、D_总、D_剩——分别为试验的回归平方和、总离差平方和以及剩余平方和;

　f_回、f_总、f_剩——分别为试验的回归自由度、总自由度以及剩余自由度;

　F₂～F(f_回，f_剩)——表示F₂服从的分布为自由度是(f_回，f_剩)的F分布。

其余符号同前。

2.采用统计量F₁对失拟平方和D_LF进行显著性检验

式中：D_LF=D_剩-D_误

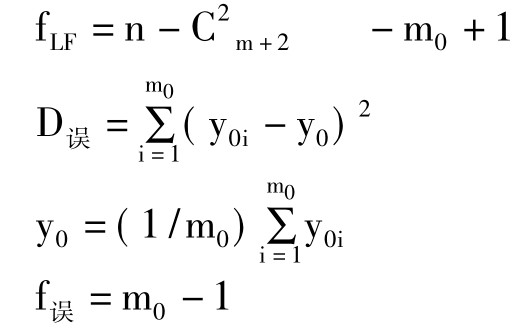
　D_LF、f_LF——分别表示失拟平方和及失拟平方和相应的自由度;

　D_误、f_误——分别表示误差平方和及误差自由度;

　y_0i——为中心点(零水平)的试验产量;

　y₀——为中心点(零水平)产量的算术平均产量;

　m₀——为中心点(零水平)的试验重复数;

　F₁～F(f_FL，F_误)——表示F₁服从的分布为自由度是(f_FL，F_误)的F分布。

3.检验顺序

设α为显著性水平。

A.若F₁＞F_1-α(f_LF，f_误)，则F₁显著，说明试验含有其他不可忽略的因素对试验结果的影响，需进一步考虑原因或改变二次回归模型，不需用F₂检验。

若F₁＜F_1-α(f_LF，f_误)，则F₁不显著，说明试验无其他干扰，可用F₂进一步检验。

B.若F₂＞F_1-α(f_回，f_剩)，则回归方程显著;

若F₂＜F_1-α(f_回，f_剩)，则回归方程不显著。

2.2.2.2.2　偏回归系数显著性检验与产量作用评价

偏回归系数显著性检验的目的是为了判别回归方程中每一个变量的作用大小。一般采用t检验方法。

当用F₁检验不显著时，构造统计量：

　　t₀=│b₀│/(a₁D_剩/f_剩)^1/2

　　t_j=│b_j│/(a₃D_剩/f_剩)^1/2

　　t_ij=│b_ij│/(a₄D_剩/f_剩)^1/2

t_jj=│b_jj│/(a₆D_剩/f_剩)^1/2　　　　　(2-2-13)

式中各符号意义同前。

若t₀、t_j、t_ij、t_jj分别大于t_1-α(f_剩)，则各回归系数显著，否则，不显著。2.2.2.3作物水肥耦合模型的优化分析

水肥耦合模型的优化分析就是利用已建的作物水肥耦合模型，通过偏回归子模型的单因素分析，寻求产量最高时的单因素最优点;在水肥试验区间取不同的水平，通过计算机模拟，寻求不同目标产量下的水肥各因素的置信区间及最优组合方案，以便生产上具体操作。其计算方法见2.2.3实例。