对立假设在红皮书第几页

三、假设检验的基本概念

参数估计关心从样本特性推论出的总体参数是否落入置信区间，而假设检验的着眼点却是落在置信区间以外的统计值。出现落在置信区间以外的统计值，从统计检验角度来说，并非一定是“坏”事，倒可能是新发现的标志。实际研究工作常遇到辨析两组样本平均数的差异问题，例如在实验研究中，实验设计总是根据假设进行的，假设预定自变量和因变量之间存在某种关联，数据分析的目标便是辨别实验组和控制组两组实验结果的差异，包括判断因变量的平均数差异是真正差异还是随机差异。所谓真正差异，指因变量的平均数变异是自变量变化（实验处理）所引起的，而非缘于随机抽样误差。如辨明是真正差异，则研究假设成立。这类研究属于假设检验。

1.对立假设

待检验假设可分两类：一类是“研究假设”，即研究者希望验证的命题；另一类是“对立假设”（null hypothesis），即研究假设的逻辑对立面。对立假设旨在作出差异产生于随机因素的解释，说明两总体的参数间无真正差异，所出现的差异不过是随机误差，“计件工资的数据录入员和计月工资的数据录入员两者的生产率平均数无显著差别”，“A厂商和B厂商提供的商品次品率平均数无显著差别”便是原研究假设的对立假设。

对立假设与研究假设相悖，如研究假设说一种方法比另一种方法更有效，对立假设则说两者有效程度一样。假设的证伪往往比证实更有力。如果从正面找出支持研究假设的论据（evidence），那充其量也只是在某种具体条件下假设被证实，并不能得出假设已被证实的一般结论。而否定的证据只要有一个，研究假设便被证伪。例如，所有质量高的管理学科博士论文作者都在博士研究生学习期间参与过企业实际研究课题，这是个研究假设。找出一位研究生曾完成过实际课题而论文质量又高，这便是证实的证据，然而，这不过是一个证据而已。如果能够发现一份高质量论文的作者从未参加过企业的课题，则上述假设便被证伪。换言之，即使有1000位参加过实际研究课题工作而论文又做得好的研究生，也不足以充分证明此假设，而找出一位不符合此条件的研究生就足以否定假设。对立假设就是根据这种思路而和研究假设相呼应地被设计的。如果对立假设被否定，便是对研究假设的有力支持。在一般情况下，如对立假设“参加和未参加过课题的研究生论文质量水平相同”被否定，便支持参加过课题的研究生论文质量高的研究假设。

设研究假设为A＞B，则相应的对立假设为A≤B。如果对立假设被否定，则支持研究假设成立；如对立假设未被否定，则研究假设未获支持。简要表示此逻辑如下：

设　A≤B（对立假设，差异不存在）。

如发现A＞B，则对立假设被否定，存在差异。否定对立假设，便是支持研究假设。

回到上面研究生论文的例子，有人可能提出“有1000名研究生证实此假设已足够，一例证伪无妨”。的确如此，这意味着研究者要选择一个风险概率，愿意承担出现失误的概率。这就涉及显著性试验问题。

2.显著性试验

置信度指真值落在容许偏差幅度（即置信区间）内的概率。研究者也可以容许出现失误，按真值落在置信区间之外的概率来设定指标，这个指标即为显著度（significance level），用α表示。如选择置信度为95％，则相应的显著度α≤0.05，若置信度为99％，则α≤0.01，表示失误机会分别小于5％和1％。与置信区间的概念相对应，相对于每个显著度都有个否定值，如α＝0.01时，标准正态分布每边相对的否定值便是2.33，标准值大于2.33的正态分布区域便是否定域（critical region）。

从参数估计的角度来看，置信度为99％时，样本Z值若大于2.33，则表示出现不能容忍的失误。前面提到，有时倒希望样本值不落在估计值的置信区间以内，由此证实两变量间关联的研究假设。所以，假设检验关心的是否定域的统计值和显著度。

显著性试验（test of statistical significance）先由主观预先选定一个显著度α，判断实验组的平均值是否落入否定域，如落入，则可断定实验组的平均值与控制组的平均值之间差异显著，证实自变量起作用的假设。

在选定显著度的条件下，有多种显著性试验方法可供选择。选取何种合适的试验方法，取决于所研究的问题，涉及到试验中数据类型（定类、定序、定距和定比）、自变量和因变量的数量等因素。

3.甲种误差和乙种误差

研究人员运用推理统计时，总是离不开两个相斥相成的假设，即“研究假设”和“对立假设”。如研究假设为“样本平均值和总体平均值之间存在差异”或“总体的变量x和变量y之间存在关联”，则“对立假设”为“样本平均值和总体平均值之间无差异”或“总体的变量x和变量y之间无关联”。假设检验时总是先检验“对立假设”，如果证据否定对立假设，则支持研究假设是真实的。

前面提到直接证实“研究假设”比较复杂甚至不可能，不如间接地否定其“对立假设”来得简明有力，所以假设检验总是围绕“对立假设”进行。上述显著性试验也是如此，对立假设如成立，则表示差异来自随机误差，研究假设便被否定。如对立假设被否定，则差异源于自变量。

研究人员就“对立假设”进行检验时离不开主观判断。如果自变量x对因变量y的影响非常明显，那也用不着应用推理和统计工具。如果说清华大学毕业生的质量比一般大学要高，一般都能接受，主观就能断定。如果说其他同一档次的大学孰高孰低，相互之间便不大“服气”，都能拿出自己比对方质量高的事例来。这种情况下才需要“假设检验”，用以判断所举出的各个具体事例是随机的还是真正差异。什么条件下才要进行统计假设检验，有赖于研究者主观判断。

如果对立假设统计检验结果为真（A＝B），研究人员判断亦为真，或对立假设为假（A≠B），研究人员判断亦为假，这无疑是正确的判断。但也可能出现错误判断的情况：一种是对立假设为真（A＝B）而研究人员判断为假；另一种是对立假设为假（A≠B），研究人员判断为真。这两种误判情况中，前一种称作甲种误差（type-Ⅰerror），后一种称作乙种误差（type-Ⅱerror）。

甲种误差是指把正确的对立假设推翻的可能性，其出现的可能性大小取决于显著度。如选择α＝0.05，则误判的可能性最大为5％。设想待检验的对立假设为“总体中变量x和y之间无关联”，而在统计检验的样本中却发现两者存在关联的数据，这在一定程度上是容许的。显著度为0.05，表示即使有5％的样本表明两者存在关联，统计检验仍得出对立假设为真的结论。当然，并不排斥数据分析人员在这种情况下会作出否定“对立假设”的判断，不过这种误判从长远来说，不会超过0.05的概率。

设想选择α＝0.01，则有1％甲种误差；如α＝0.001，则误判率最多只0.1％。照此推论，α取值更小如0.00001岂不更好。的确，α非常小时出现甲种失误的概率很小，不再会否定真实的对立假设，但这时出现乙种误差问题。

乙种误差指把错误的对立假设视为真实而接受的可能性，钟伦纳形象地把甲种误差比喻为“杀错良民”，将同类样本视为异类，把乙种误差比喻为“引狼入室”，将异类样本视为同类。随着甲类误差减小，显著度愈小，随机抽样误差的容许偏差范围增大，要求两种平均数之间的差异幅度增大。例如，设想在α＝0.05的情况下，两平均数差异值为13已经可表明总体的真实差异，如选择α＝0.001，为了照顾平均数不落入α＝0.001所相应的±3.05σ范围内，则要求差异值增加到20（σ＝13/Z＝13/1.96＝6.6，6.6×3.05＝20），否则仍然认为是随机抽样误差和对立假设为真。如实际分析的平均数差异值为15，按α＝0.001的要求，则应视对立假设为真，尽管事实上存在真实差异（15＞13），这就将本可否定的对立假设误判为真，增加了乙种误差。

甲、乙两种失误相互制约，研究者要根据研究问题性质分辨两种失误的重要程度，预先选定显著度α值。例如评价一种新工艺方法或新管理方案，从研究开发人员的角度来说，偏向于接受较大的甲种误差，希望条件不要卡得太严，承认新方法产生的效应，故选用的α值较大。而从用户的角度则偏向于接受较大的乙种误差，希望排除尽可能多的随机抽样误差，“安全系数”大些，更有把握地保证样本平均数差异真正符合研究假设，故选用的α值较小。不过大多数研究中采用α＝0.05，这是一般情况下各方面都能接受的水平。

有一个容易出现的误解，以为否定对立假设就是证实了研究假设。否定或肯定一个对立假设只是从概率的角度表明支持或不支持某个研究假设，否定对立假设只是说两组平均值可能存在真正差异，但还不能说这种真正差异的来由就是研究假设中的自变量所引起的，也可能是其他因素导致的差异。如果不能否定对立假设也不能就说研究假设已被证伪，可能是假设的测试次数还不够多。

4.单边检验和双边检验

显著性试验常采取双边检验（two-tailed test），对立假设陈述如为A＝B，双边检验则考虑正态分布正负两个方向出现差异的可能性。例如，一组平均数可能高于也可能低于另一组平均数（A＞B或B＞A），一个新方法可能提高效率也可能还比不上原方法的效率。而单边检验（onetailed test）则设想只能在正态分布的一个方向出现差异，如假设新方法只会提高工作效率，即A＞B，此时相应的对立假设为A≤B。以前面提到的对立假设“计件工资与计月工资的数据录入员的生产率无差别”为例，在双边检验的条件下，研究假设可表述为“计件工资与计月工资的录入员的生产率有差异”，表示计件工资人员可以高于或低于计月工资人员。如是单边检验研究假设，则为“计件工资录入员比计月工资的录入员生产率要高”，此时研究人员设想计月工资人员不大可能高于计件工资人员的生产率。

从正态分布曲线来看，否定域可以预设在正态分布的两端或任一端，如设在两端则为双边检验，设在单端则为单边检验。单边检验的好处是在同样的显著度下，单边检验的否定值是双边检验否定值之半，因而较易否定对立假设。

研究者采用单边检验时，一定要有十分把握认定差异只会在单方向发生，否则就会冒事与愿违的风险。如果能用单边检验，其好处是比较容易找到显著差异。例如显著度α＝0.05时检验两平均数的差异，如系双边检验，便要容许出现正或负值，亦即第一组平均数可能高于第二组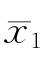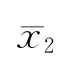－为正数，也可能相反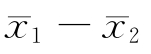为负数，α的值0.05也要相应分为两半，各为0.025。而0.025意味着容许的甲种误差小于单边检验0.05的一半，实现相对比较困难。表5-18表示在几种常用显著度情况下，单边和双边检验时的临界否定值（Z），当样本的标准值大于此Z值时，即可推翻对立假设。

5.自由度

在选定显著度、单边或双边检验进入显著性试验时，要根据规范的抽样分布表格来判定两组平均数差异是否显著，这些表格设计除考虑显著度和单、双边检验外还须考虑自由度（degree of freedom）。自由度是指可以自由变动数值的样本数目。自由度的概念可以通过一个例子来说明，设想请你说出五个数目，你可随意说“12，18，20，30，10”，这时，N＝5，你可有五种选择或者说五个自由度。如果给你附加一个条件，即五个数的平均数要等于25，这时你不得不按此平均数来更换其中一个数，例如将10改成45，这样，原来的五个自由度现在只能有四个，即（N－1）个。各种显著性检验方法有各自计算自由度的公式，皮尔逊积矩相关系数算式中自由度为N－2。

表5-18　单边和双边检验的Z值

6.参数检验和非参数检验

不同的显著性检验适用于不同类型的数据。从尺度类型角度可将显著性检验分为参数检验（parametric statistical test）和非参数检验（nonparametric statistical test）。数据为定距和定比类型时对应的检验方法为参数检验，而定类和定序数据以及总体偏态分布或分布情况不明情况下，对应的检验方法为非参数检验。采用参数检验时须符合一些前提条件，包括：总体的分布类型已知（如总体服从正态分布）；变量度量系用定距或定比尺度；抽样的独立性，总体的各个成员都有同等的被选择的机会；所比较的两组样本的总体变异状况即标准差相同，等等。

上述前提条件中，对总体分布类型的要求，管理研究中有些变量还能符合，或稍许放松便可作出显著性判断；定距定比尺度的变量在管理研究中也常用到，如现金流等；独立性条件在实际中最值得注意把握。

非参数检验处理总体分布未知时的检验问题，因而，根据变量分布曲线作出判断的方法，应用便比较困难。但统计技术中也有多种非参数检验方法如x²检验法等。管理研究所处理的变量大部分属于定序或定类尺度，这可以说是管理研究的特色。尽管有些场合下，定序尺度的变量可转换为定距尺度（如问卷答案的处理），非参数检验的问题仍会经常遇到。在大样本情况下，多种非参数检验的效力也可以达到参数检验的要求。