经济活动决策常用的数学方法

第四节　经济活动决策常用的数学方法

一、非确定性决策的数学方法

非确定性决策指决策者知道哪些情况可能发生，但不知道各种情况发生的概率的条件下进行的决策。这种决策是比较困难的，影响决策的关键主要是决策者以决策标准的掌握。不确定型决策的标准一般有如下3种：

（一）最大最大标准决策法

最大最大标准指在所有的备选方案中，比较各种方案的最理想状态，以其中最为理想的状态为标准进行决策。这种决策标准称之为不确定状态下的乐观主义者行为准则。

（二）最大最小标准决策法

最大最小标准决策法指在所有的决策方案中，比较各个方案可能出现最坏状况，以其中最小损失为标准进行决策。这种决策标准表现了不确定性状态下的悲观状态，是悲观主义者的行为准则。

（三）最小最大遗憾标准决策法

这种方法的原则是：假定决策者在各种备选方案中做出了选择之后，在执行决策时发现，如果按当前的实际情况或称自然状态，不选择该方案，而选择其他备选方案。收益会更高或亏损之间的差，会使决策者感到遗憾，未被选择的方案与选择的方案二者之间的损益值，可以看作是决策者遗憾的程度，这个值就被称为遗憾值。最小最大遗憾标准法就是以最小遗憾值为标准对方案所进行的选择。

二、风险型决策

风险型决策的具体方法比较多。在企业的经营活动中，比较常见的有期望利润标准法、期望损失最小化法、边际利润法和决策树法。下面仅仅介绍最为常用的决策树法。

决策树是一种形象的说法，它是利用一种形如树枝的图形，帮助决策者决策的一种方法。决策树法也是一种风险型决策方法。使用这种方法所需要的条件是决策者知道各种方案在各种不同状态下的损益值，以及每种方案在各种情况下发生的概率值。决策的基准仍然是期望利润最大化。决策树的图形通常如图7—2所示：

图7-2　决策树

决策树法的程序一般是：

1．绘制决策树形图，一般从决策点开始，向右展开，即首先绘出决策点，用符号口表示，然后引出方案分枝，在方案分枝处绘出自然状态结点，用○表示，然后再绘出各种自然状态分枝，并标上概率值。

2．计算期望值，将各方案的期望值相加。

3．比较不同方案，选出期望值最大的方案。

现用一个例子来简要地说明决策树法的基本步骤。长城公司必须决定建造一座大的或小的工厂来生产一种新的电视机，其期望的市场寿命为10年。建造一座大厂并投入生产需要花2800万元，建造一座小厂并投入生产只需花1400万元。公司对10年间销售的情况估计如下，高需求的概率为0．5，中需求的概率为0．3，低需求的概率为0．2；在高需求情况下，建一座大厂可年获利1000万元，建一座小厂则只能获利250万元；在中需求情况下，建一座大厂年获利为250万元，建一座小厂则每年可获利45万元，因为此时损失和其他费用大大降低，在低需求的情况下，建一座大厂因没有充分利用生产能力每年亏损200万元，而建一座小厂则可年获利550万元，因此时的市场需求主导工厂规模相当。试问长城公司是应该建一座大厂还是建一座小厂？

长城公司决策的备选方案及其约束条件，以及期望利润（包括亏损）可用图7—3进行计算。

由图7—3可知，当选择建大厂的方案时，长城公司的期望利润总额为3600万元，当选择建厂的方案时，期望利润总额为2300万元。那么，按决策树法的决策标准，长城公司应选择建大厂的方案。

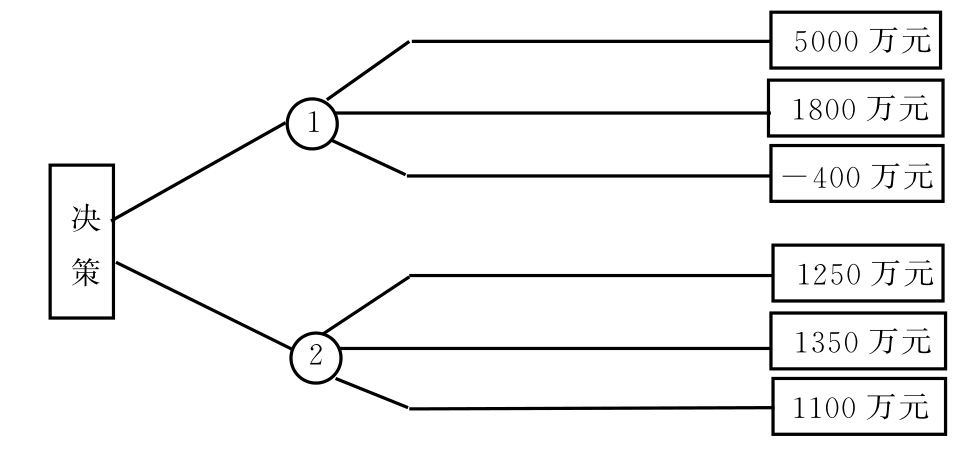
图7-3　决策树计算结果

从上面的决策分析可知，以数学原理为基础的决策都是以期望值为标准的，如果方案A的期望利润比B高，那么决策人就应选择方案A。同理，如果方案C的期望损失大于D方案，决策人就应选择方案A。同理，如果方案C的期望损失大于D方案，决策人就应选择D。但这一准则在具体的决策活动中应注意其适用范围。如果一个企业资产有一个生产爆炸品的车间，价值1000万元，这个车间发生爆炸的概率为万分之一。由此可知，该车间的期望损失为1000万×1／10000＝1000元。如果在保险公司投保，保险费率为万分之一点五，即保险费为1500元。从对期望值的比较来看，保险费的支出大于其期望亏损。在这种情况上下，企业应不应该投保？显然，如果企业领导人认为一旦发生爆炸，1000万元的财产损失太大了，就可能会投保。此时就不再是按期望值标准进行决策的了。阐述这一例外情况是想说明，采用风险性决策的数学方法进行决策计算之后，还应将期望结果与组织所面临的实际情况结合起来全盘考虑，再做最后的决断。这也表明，数学模型计算的结果只是决策的重要依据，但不是惟一的依据。

三、博弈论与竞争性决策方法

（一）博弈的概念

博弈是当今经济学和管理学中使用频率颇高的一个概念。博弈，从字面上理解就是对局、斗智的意思。博弈论是当代发展特别快，在经济学、管理学中运用特别广泛的一门新兴科学。它是一门研究在一定决策主体相互作用的环境中，特定主体做出最优选择的科学。

博弈论在英文中是Game theory，也可以译为游戏理论、对策论。博弈是现代社会中最常见的一种现象，如在竞争性的体育运动中，如足球、篮球等球类运动、棋类运动等都可以抽象为博弈活动。现代企业的经营也是博弈活动。一个企业必须参与市场的竞争，必须根据市场的竞争状况做出一定的决策。当这个企业在这样思考和决策时，市场上其他的企业同样会这样思考和决策。因此，一个企业的决策可以说是时时刻刻在博弈，它要根据市场的竞争状况做出合适的决策。反过来，企业的决策又会影响其他的企业的决策，其他企业会针对这个企业的决策做出竞争的对策，这样原来企业所面临的环境就又发生了变化。在这样的状态下，企业应当怎样决策才是最合理的？这就是决策论所要研究的问题。

（二）博弈的类别

1．按照博弈方之间是否达成对各方都有约束力的协议，可以分为合作博弈与非合作博弈。在人们相互影响的活动中，如果参与方之间签订了一个对各方都有约束力的协议，这时的博弈就是合作博弈；如果没有，就是非合作博弈。例如在一个市场上，两个大企业之间结成卡特尔或者是订有其他的协议，对于这两个大企业来说，要解决的问题就不再是如何针对对方决策，而是要考虑如何分享合作所带来的剩余问题。合作博弈又称之为非竞争性博弈。如果在市场上不存在类似的协议，每个企业都是针对竞争对手来做出自己的价格、产量决策，就是非合作博弈，非合作博弈也就是竞争性博弈。当前的博弈论主要研究的是非合作博弈，在管理学中运用最广泛的也是非合作博弈。

2．按照博弈的结果可以将博弈分为零和博弈与非零和博弈。零和博弈指的是参与方在博弈之后其总和不会发生变化的博弈。如在一个规模不变的市场上，一些企业的市场占有率提高，必然伴随着其他一些企业的市场占有率的下降。在这样的市场上，企业的博弈就是零和博弈。零和博弈最基本的特征就是竞争双方的利益得失相等。非零和博弈是竞争之后的总结果与竞争之前的总结果不相等的博弈。如存在潜在扩大的市场，竞争的双方中有一方率先降价，导致另一方竞争降价，使得市场需求扩大。如果该产品的价格弹性充足，降价使企业的销售额与利润都增加，则是双赢的博弈；如果该产品的价格弹性不足，降价竞争使得双方的销售额与利润都减少，则是无赢家的博弈。

在竞争性的市场上，零和博弈的情况比较少见，因为从长期动态的立场来看，零和博弈更是不能存在的。非零和博弈的结局也并非仅仅只有上述两种，而是有多种。

3．按照参与者行动的顺序可以分为静态博弈与动态博弈。静态博弈指的是在博弈中，参与者同时选择行动，或者是不同时行动，但是后行动者并不知道先行者采取了什么样的行动，仍然是按照自己的决策行动；动态博弈指的是参与者的行动不仅有先后顺序，而且后行动者能够观察到先行动者所做出的决策，然后采取行动决策。在静态博弈中，决策过程是一次性的；在动态博弈中，参与方的决策是循环往复的。

4．按照参与博弈的人数的多少，可以分为二人博弈和多人博弈。在管理决策中运用比较多的是二人零和博弈理论。

（三）竞争性博弈决策模型的基本要素

1．参与者，指参与博弈的主体，在博弈论中，参与者是广义的。在企业的市场竞争中，利益和目的一致的参与者只能算作一个参与者。一般假定，博弈的参与者是追求自己的效用最大化的。在一定的环境约束下，按照效用最大化的原则决策。

2．策略集，指参与者的决策变量，或者是要做出的决策。全体参与者的行动构成的结合就称之为策略集。

3．支付函数，指参与者从博弈中获得的收益水平。

参与者、策略集和支付函数是竞争性决策模型的三个基本要素，这三个要素确定了，竞争性决策的问题也就确定了。

（四）博弈论的应用范围

博弈论在今天的决策中应用相当广泛，特别是对于市场经济条件下企业的经营决策有着直接的指导作用，因为企业的经营决策本质上就是一个与竞争对手的博弈过程。不过，博弈论在一般企业的经营决策中应用，成本比较高。因为这个理论的运用需要专家指导，需要建立复杂的模型和进行复杂的分析。但是，我们必须看到，随着科学的决策手段的使用，博弈论在未来企业的经营中将越来越广泛地运用。

本章阅读书目：

1．（美）赫博特·A·西蒙：《管理决策新科学》，中国社会科学出版社1985年版。

2．MBA核心课程编译组：《经营战略》，中国国际广播出版社1997年版。

3．（美）迈克尔·波特著：《竞争战略》，华夏出版社1997年版。

4．（美）彼德·F·德鲁克：《面对未来的抉择——机会与成功》，工人出版社1989年版。