长期投资决策评价的方法

第四节　长期投资决策评价的方法

按照是否考虑资金的时间价值，长期投资决策的评价指标可以分为贴现指标和非贴现指标。

一、贴现指标

（一）净现值

净现值（Net Present Value，缩写为NPV）是指从投资开始直至项目寿命终结时现金流入量与现金流出量按预定贴现率折现的现值之差。贴现率可以是企业的资本成本，也可以是企业要求的最低收益率水平。净现值的计算公式为

其中：n为项目经济寿命期，r为预定贴现率，NCF_t为第t年的净现金流量，NII为项目的净增量投资额。

净现值的决策标准是：投资项目的净现值大于零，接受该项目；净现值小于零，则放弃该项目。多个互斥项目进行选择时，选取净现值最大的项目。

例8-11：以上述启明公司的项目为例，假定该项目的折现率为8%，那么

NPV大于零，该项目可行。

（1）NPV体现了项目的投资效益。从货币价值增量绝对额的角度来考察项目，符合企业价值最大化的目标。

（2）NPV是预定贴现率r的函数，从其计算公式中可以看出，NPV本质上是假定预定贴现率r为自身的增值率，按此增值率增值后，多余现金流量按此贴现率贴现的现值。因此，贴现率r的确定是净现值法的关键。

（3）对于投资期限不同的互斥方案，NPV比较的效益期限不同。因此，对这类方案不适合用NPV比较。这时，可使用年均净现值指标（A NPV），它等于净现值除以对应的年金现值系数，用以表示每年所获得的净现值，从而可以对不同期限的项目进行比较。

（二）内含报酬率

内含报酬率（Internal Return Rate，缩写为IRR），是使项目的未来现金流入量的折现值等于未来现金流出量的折现值时的贴现率，即净现值为零时的贴现率。它反映了一个投资项目自身的投资报酬率。计算公式为

内含报酬率的计算过去通常使用插值法，计算较为繁琐，但现在可以通过计算机软件（如Excel）快速地获得，这极大地推动了该指标在实践中的应用。

内含报酬率的决策标准是：如果项目的内含报酬率大于企业的资本成本，则接受该项目；如果内含报酬率小于企业的资本成本，则放弃该项目；多个互斥项目进行选择时，选取内含报酬率最大的项目。

仍以启明公司的项目为例，通过计算可得其内含报酬率为46．26%，高于其资本成本8%，因此，该项目可行。

内含报酬率指标的特点：

（1）IRR是由特定的现金流量所确定的。即只要达到预定的现金流量，无论实际的再投资收益率为多少，内含报酬率都是确定的。

（2）IRR的计算与基期无关。这可以从计算公式的特点中推出。在等式两边同时乘以（1＋IRR）ⁱ（i为任意正整数）等式变为

该等式的含义是将现金流入与现金流出按IRR同时折算至第i年末时仍相等。即无论将现金流量折算至哪一年，只要流入量与流出量相等，其折现率都等于IRR。

（3）IRR假定各个方案的所有中间投入可按各自的内含报酬率进行再投资而进行增值。理论界通常认为这与实际有所不符。如某方案的现金流量如图8-5所示。

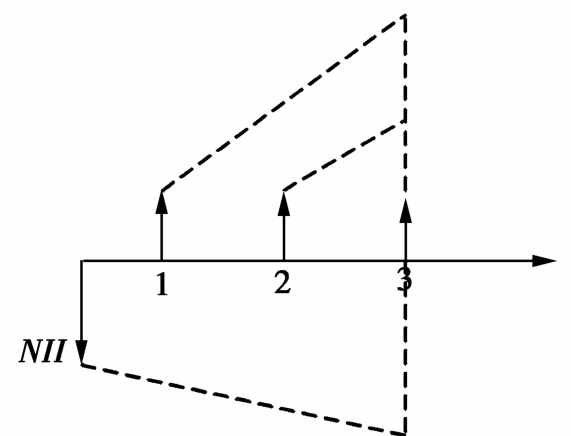
图8-5

由于IRR的计算与计算基期无关，因此，可将所有现金流量折算至最后一年末。如图8-5所示，内含报酬率也可理解为使一个投资方案的初始投资额的终值与各年的净现金流量终值之和相等的收益率。这样，方案的净现金流量都是按其IRR进行再投资，导致不同方案有着不同的投资收益再投资假定，从而削弱了IRR的可比性。但是，这并不影响IRR的客观性，只要预计的现金流量实现，那么，无论实际再投资收益率为多少，都不会改变其内含报酬率。

（三）外部收益率

外部收益率（External Return Rate，缩写为ERR）是根据内含报酬率的再投资假设的不足而提出来的，它是使一个投资项目投资额的终值与各年的净现金流量按预定收益率计算的终值之和相等时的收益率，计算公式为

其评价规则与IRR相似：对单一项目的可行与否决策，ERR大于资本成本时，方案可行，否则不可行。对多个项目的选择决策中，取ERR最大的方案。

外部收益率的主要特点：

（1）经济含义较明显，即通过一项投资的终值与现值的比较得出其增值率。

（2）ERR是预定收益率的函数。它以预定收益率作为再投资报酬率，受r的准确性的影响，其取值具有一定的主观性，并且人为预计未来现金收益的报酬具有很大的不确定性，很难为人所信服，这也是ERR受人攻击，难以普及的重要原因。

（四）获利指数

获利指数（Profit Index，缩写为PI）是指投资项目未来各期现金流量的折现值与初始投资额之比。其基本特点与净现值类似，只是从投资效率的角度来考察项目，其计算公式为

获利指数的决策准则是：当投资项目的获利指数大于1时，选取该项目；当获利指数小于1时，放弃该项目；当有多个互斥项目供选择时，选取获利指数最大的项目。

对于启明公司的项目：

获利指数为2．31，代表1元的现金投资可以产生现值为2．31的现金流入，因此项目可行。

对于投资额不同的方案，仍然可以利用PI比较各方案的投资效率，但该指标仍没有考虑期限的因素，同NPV指标一样，对不同期限的互斥方案仍不适用。

二、非贴现指标

（一）投资回收期

投资回收期（Payback Period，缩写为PP）是指收回全部初始投资所需要的时间，通常以年为单位。这个指标可以衡量初始投资额的回收速度的快慢。计算公式为

例8-12：对于启明公司的例子，计算过程如表8-2。

表8-2　投资回收期计算表　　　　　　单位：元

显然，回收期应在1年与2年之间，可按下式计算：

即项目可在1．95年的时候收回全部投资额。回收期的决策过程很简单，选择一个企业可以接受的回收期，如2年，则所有回收期小于或等于2年的项目都可行，大于2年的项目则不可行。

回收期法的优点是易于理解，计算简单，但同时存在明显的不足：

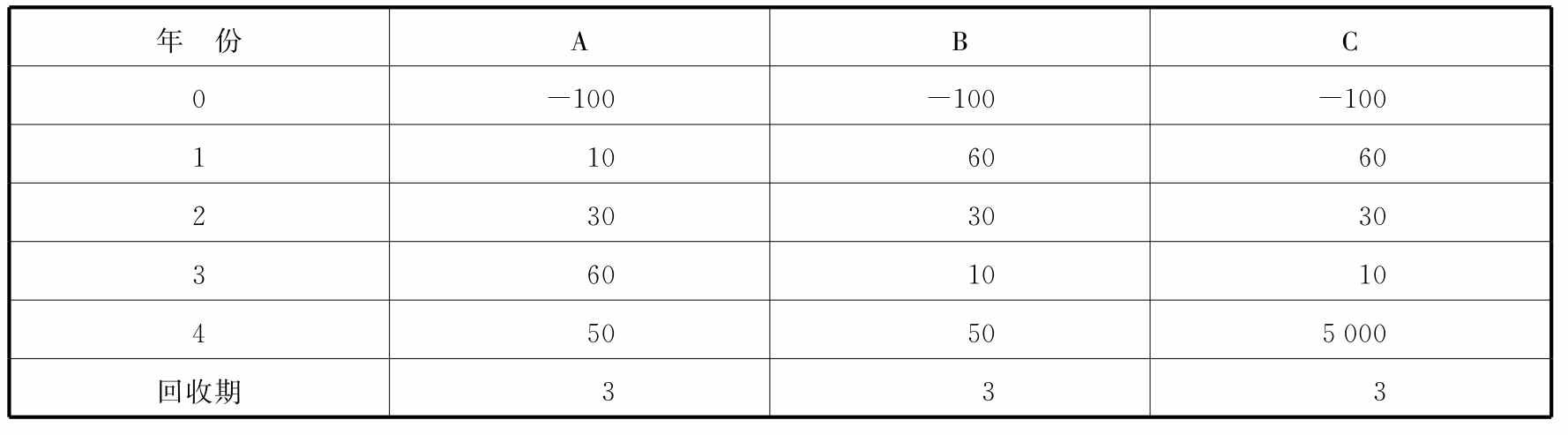
（1）回收期法不能体现回收期内现金流量的分布先后。如表8-3中所示，项目A与项目B，现金总额相同，但项目B的现金流的分布是先大后小，因此净现值一定高于项目A，而两者的回收期相同。这是由于回收期法没有体现资金的时间价值。

（2）回收期法没有考虑超过回收期的那些现金流量。如表8-3中项目B与项目C，显然，项目C要优于项目B，但两者的回收期却相同。这是因为回收期法不能反映超过回收期以后的现金流量。

（3）回收期法的决策依据主观臆断，没有客观准确的参照标准可供选择，只能根据企业管理人员的主观判断。

表8-3　回收期的计算

由于回收期法的不足，一些决策人员又提出了新的方法，称为折现回收期法（Discounted Payback Period，缩写为DPP），这种方法先对现金流进行折现，然后计算折现后现金流量的回收期。如对表8-4中项目A按8%的折现率计算折现回收期。

表8-4　折现回收期法计算表

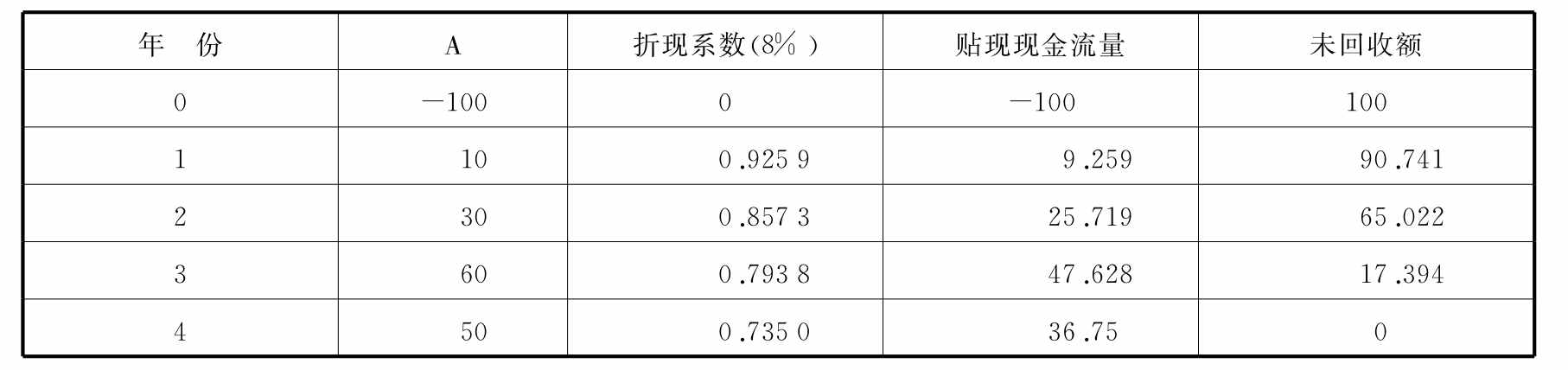
贴现回收期在3年和4年之间，具体计算如下：

由于贴现会使现金流量变小，所以折现回收期一定会大于相应的回收期。

折现回收期法虽然考虑了时间价值的因素，但仍没有反映回收期后的现金流量情况，判断标准依然主观，并且计算方法也变得较复杂，因此，实践中并不常用。

（二）会计收益率

会计收益率（Accounting Return Rate，缩写为ARR）指标是指投资项目经济寿命期内的平均税后利润与净增量投资额之比。它采用会计报表上的数据，易于理解，在实际工作中也有广泛应用，但与投资回收期一样，它没有考虑货币的时间价值，属于静态指标。

其中：A NR表示年平均净收益，它等于年均营业净现金流量减去年均折旧额；NII表示净增量投资额。

在采用会计收益率法进行投资方案评价时，应事先确定一个企业要求达到的会计收益率，在进行采纳与否的决策时，高于要求达到的收益率则可行，否则放弃。在多个方案的互斥选择决策中，选用会计收益率最高的方案。

三、投资决策指标的比较

（一）NPV与IRR的比较

对于独立方案而言，各方案之间互相独立，彼此互不影响，对这类方案的决策，主要是考虑其经济上是否可行。此时，NPV、IRR会得出相同的结论。

仍以启明公司为例，我们可以得到不同折现率条件下，NPV的各个取值（见表8-5），从而可以绘出NPV曲线图（见图8-6）。

表8-5　NPV变化表

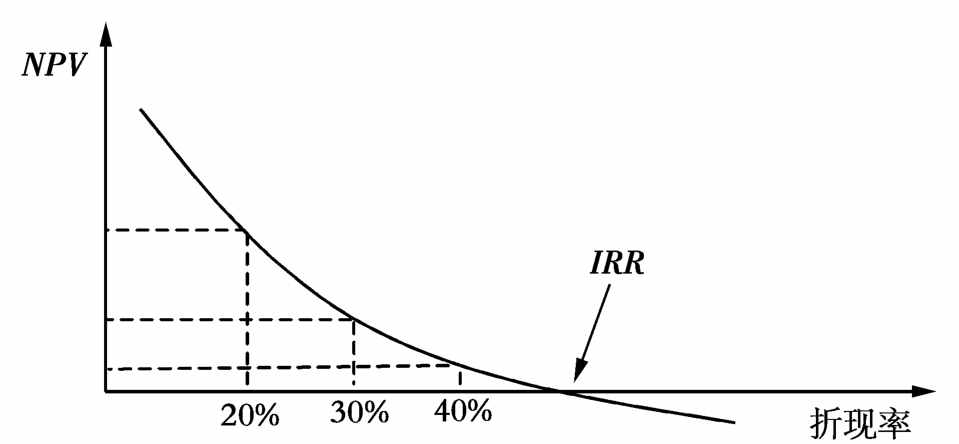
图8-6　NPV曲线图

从NPV曲线图中可以看出，IRR是NPV曲线与横轴的交点所在的折现率。当折现率小于IRR时，NPV大于零；当折现率大于IRR时，NPV小于零；当折现率等于IRR时，NPV等于零。因此，对单一项目的可行与否决策或独立项目的选择，两者的结论总是一致的。

而对于互斥方案，两个指标可能出现相互矛盾。考虑下面两个项目。

例8-13：两个项目A、B的预测现金流量如表8-6所示。

表8-6　两个项目的现金流量预测　　　　　　单位：元

图8-7　项目A和项目B的NPV曲线图

我们可以画出两个项目的NPV曲线，如图8-7所示。

如图8-7所示，项目A的IRR为16．04%，项目B的IRR为12．94%。当折现率为12．07%时，两个项目的净现值相等。如果按照IRR进行选择，应选择项目A。

当折现率小于12．07%时，项目B的净现值要大于项目A的净现值。因此，按照净现值法则，应选择项目B；而当折现率大于12．07%时，项目A的净现值大于项目B的净现值，应选择项目A。因此，按照净现值选择方案，关键是选取的折现率的高低。

在上例中，两个项目投资规模不同，以及各期现金流量的分布不同，从而造成两个项目的净现值曲线在第一象限内交叉。当资本成本低于12．07%时，两种方法得出不同的结论。造成净现值法和内含报酬率法所得出的结论相矛盾的根本原因，在于两种方法的再投资假设不同。净现值法下的再投资报酬率是资本成本，而内含报酬率法下的再投资报酬率为项目的内含报酬率，即假定项目产生的现金流量能以该项目的内含报酬率进行再投资。通常认为，在资金充足的市场上，资本成本应是投资者要求的均衡收益率，故以资本成本作为再投资假定更加合理。当净现值法和内含报酬率法产生矛盾时，人们更愿意采用净现值法作为评价指标。

另外，还可以使用增量内部收益率法解决两者的矛盾，它是选择大投资额的项目时，所增加的那部分投资的内部收益率，即计算两个项目的差额现金流量的内部收益率。为使差额现金流量的初始额为负，我们使用项目B减项目A的现金流量，如表8-7所示。

表8-7　差额现金流量　　　　　　单位：元

差额现金流量的内含报酬率为12．07%，当资本成本低于12．07%时，则多投资的那部分是值得的，应选择B项目。当资本成本高于12．07%时，多投资的部分不能弥补资本成本，因此应选择A项目，选择的结果和净现值法是一致的。

（二）净现值法与获利指数法的关系

对于独立项目的评价，净现值法和获利指数法得到的结论是一致的，只是从不同方面反映项目的获利能力。净现值法侧重反映项目的效益额，而获利指数侧重反映项目的效率高低。

对于互斥方案的选择决策，两者可能得到不同的结论。这是因为净现值是一个绝对值指标，而获利指数是一个相对指标。用NII表示投资额，两者的关系表示为

NPV＝NII×（PI－1）

从公式可以看出，NPV的大小取决于该项目的投资规模和获利指数，因此，对于规模相同的两个互斥项目，两个指标的结论应是相同的。而对规模不同的两个项目，如果获利指数相同，规模较大的项目会带来更大的净现值。更高的净现值符合企业价值最大化的目标，因此，在这种情况下，应选择净现值最大的方案。

四、折现率的确定

我们知道，企业投资项目的回报必须满足项目投资者所要求的收益，才能融通到所需的资金。因此，当管理者在评估一个项目时，他们应该确定该项目所增加的现金流能否补偿所增加的风险。换句话说，管理者应该明确，在项目风险既定的情况下，提供多高的回报才能从现在的金融市场上融通到所需的资金。投资者所要求的回报就是企业为该项目进行融资的资本成本，也是管理者在评估该项目预期现金流的现值时应使用的折现率。如果项目的预期报酬高于投资者要求的收益率，那么该项目就应该被采纳，否则，就应该被否决。

大多数企业在对新项目进行融资时，都要对各种资金来源进行组合，各种资金来源的比例取决于企业的目标资本结构，这种融资组合的平均资本成本就应该作为项目的折现率。首先，根据项目的风险和当前金融市场的状况计算出各项资金来源的成本，即个别资本成本。其中，债务资金来源的成本称为债务资本成本，权益资金来源的成本称为权益资本成本，然后结合项目的目标资本结构，我们就可以计算出该项目资金的加权平均资本成本。加权平均资本成本的计算公式为

其中：K为加权平均资本成本，K S为权益资本成本，K B为税前债务资本成本，T为所得税税率，B为债务资金的价值，S为股东权益价值。

这个加权平均资本成本是企业为该项目进行融资的平均成本，因此通常被用来作为长期投资决策评价过程中的折现率。应该注意的是，项目的折现率选择应该与现金流量的风险相对应，如何采用项目的实体现金流量，则应该使用平均资本成本作为项目的折现率；如果使用股权现金流量，则应该使用权益资本成本作为项目的折现率。实体现金流量与股权现金流量的关系为

股权现金流量＝实体现金流量－债权人现金流量

实体现金流量是项目所产生可供股东和债权人共同分配的现金流量，债权人现金流量包括应支付给债权人的税后利息额以及本金额。而股权现金流量是实体现金流量中扣除了给债权人的现金流量之后的剩余现金流量。