正态总体方差σ的假设检验（χ－检验）

要求检验假设

现在分别对μ已知和μ未知两种情形进行讨论．

1．μ已知，σ2的假设检验（χ2－检验法）

（1）对于假设选取检验统计量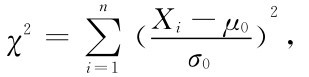容易证明在H0成立时，χ2服从自由度为n的χ2分布，既χ2～χ2（n）．

在H0成立时，χ2不能过大，也不能过小．对给定的显著性水平α，由于

故H0的拒绝域为W＝｛χ2＜χ1－α／2（n）或χ2＞χα／2（n）｝．

（2）类似地，对于假设检验大一些较合理，χ2过小不合理，χ2小过是小概率事件．对给定的显著性水平α，由于P｛χ2＜χ1－α（n）｝＝α，故H0的拒绝域为W＝｛χ2＜χ1－α（n）｝．

（3）对于假设检验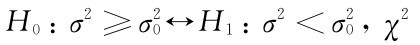小一些较合理，χ2过大不合理，χ2过大是小概率事件．对给定的显著性水平α，由于P｛χ2＞χα（n）｝＝α，故H0的拒绝域为W＝｛χ2＞χα（n）｝．

例8．2．5 设某砖厂生产的砖的抗断强度X～N（32．50，1．21），某天从该厂生产的砖中随机抽取6块，测得抗断强度如下（单位：kg／cm2）：

32．56　 29．66　 31．64　 30．00　 31．87　 31．03

以显著性水平α＝0．01，检验这天该厂生产的砖的抗断强度的标准差是否为1．1kg／cm2？

解 这里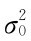＝1．21，而μ＝μ0＝32．50已知．提出假设检验：

由于显著性水平α＝0．01，查表得＝12．6，

拒绝H0，接受H1，即这天该厂生产的砖的抗断强度的标准差不能认为是1． 1kg／cm2．

2．μ未知，σ2的假设检验（χ2－检验法）

（1）对于假设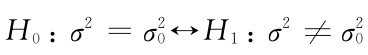

在第七章中已经看到：样本方差S2是σ2的无偏似然估计．当原假设H0成立时，S2应该在的附近，比值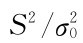不能太大也不能太小．则在原假设H0成立时，选取检验统计量

对给定的显著性水平α，由于P｛χ2＜χ1－α／2（n－1）｝＝P｛χ2＞χα／2（n－1）｝＝α／2．

故H0的拒绝域W＝｛χ2＜χ1－α／2（n－1）或χ2＞χα／2（n－1）｝．

（3）对于假设检验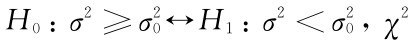小一些较合理，χ2过大不合理，χ2过是大概率事件．对给定的显著性水平α，由于P｛χ2＞χα（n－1）｝＝α，故H0的拒绝域为W＝｛χ2＞χα（n－1）｝．

例8．2．6 某类钢板每块的重量X服从正态分布，其一项质量指标是钢板重量的方差不得超过0．016（kg2）．现从某天生产的钢板中随机抽取25块，得其样本方差为0．025（kg2），问在显著性水平α＝0．05下，该天生产的钢板重量的方差是否满足要求？

解 由题意建立假设检验：H0：σ2≤0．016↔H1：σ2＞0．016．

此处n＝25，对显著性水平α＝0．05，查表得

现在计算

故拒绝H0，认为该天生产的钢板重量的方差不满足要求．