各态历经性

对于平稳随机过程而言，最重要的两个特征指标是均值函数和相关函数（协方差函数），如何根据实验记录确定均值函数和相关函数呢？

首先注意到，若重复大量观察一个平稳过程，就可以获得足够多条样本函数，再用数理统计中矩估计法，就可以估计均值函数和相关函数。即

这样的估计有两个间题值得注意，首先，根据大数定律，对于任给的ε＞0，有

并且对于任给的实数，就要求观察足够多条样本函数，而这在实际情况中几乎是难以办到的；其次，对于获得的样本函数，估计时只用到一两个点，很“浪费”。因此考虑有没有可能通过一次足够长时间的观察，用一条样本函数关于时间的平均来估计均值函数和相关函数呢？答案是对于平稳过程，如果满足一定的条件，就可以用一条样本函数关于时间的平均来估计均值函数和相关函数。这就是本节要讨论的各态历经性。为此先给出随机积分的概念。

定义13.2.1　设为二阶矩过程，上确定性函数，若对X（t）的任一样本函数上可积，记：。由于随机过程的样本函数不同，因此积分值是一个随机变量。

但有时候不能保证对于所有的样本函数，上都是可积的，这就需要引入均方可积的概念。

定义13.2.2　设为二阶矩过程，上确定性函数，将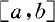分割，。若存在随机变量Y，使得，称上均方可积。

注　当两种定义的积分都存在时，它们相等的概率为1，故今后不再加以区别，记为。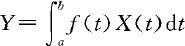

均方可积准则　上均方可积的充要条件是

存在。特别地，X（t）在巨［a，b］上均方可积的充要条件是上可积。

均方积分性质　设f（t）X（t）在［a，b］上均方可积，则有

证略。

定义13.2.3　设为平稳过程，

称为过程的时间均值；对于任给的τ，

称为过程的时间相关函数。

定义13.2.4　设为平稳过程，

以概率1成立，则称过程的均值具有各态历经性；

（2）若对于任给的实数τ，

以概率1成立，则称过程的自相关函数具有各态历经性；

（3）若X（t）的均值函数和自相关函数都具有各态历经性，则称X（t）是（宽）各态历经过程（ergodic process）。

例13.2.1　设，其中α，ω是正常数，θ为随机变量，。证明是各态历经过程。

证明　由第十章例10.3.1知，是平稳过程，

根据各态厉经过程的定义知，随机相位正弦波过程是各态厉经过程。

对于随机相位正弦波来说，所有样本函数的差异只是相位的不同，而每一条样本函数都“历经”了状态空间［－a，a］间的各个状态，从而是各态历经过程。它的每一条样本函数关于时间的平均都是一样的。

例13.2.2　设，其中ω是正常数，A，θ为相互独立的随机变量，。证明是平稳过程，判断是否为各态历经过程。

因此的自相关函数不具有各态厉经性，从而不是各态历经过程。

思考一下这个正弦波的样本函数有什么差异，每一条样本函数的时间均值是一样的鸣？样本函数的时间相关函数为什么不一样呢？

例13.2.3　设是随机变量，。证明是平稳过程，的均值不具有各态历经性。

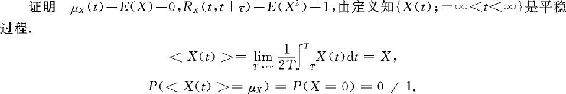
所以的均值不具有各态历经性。

注意到此过程只有两条样本函数，。状态空间只有两个值｛1，－1｝，但每条样本函数只取一个状态，所以均值也不具有各态历经性了。

下面讨论一个平稳过程均值和自相关函数各态历经性的充分必要条件。

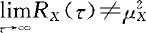推论13.2.1　对于平稳过程存在的条件下，若，则X（t）的均值具有各态历经性；若，则X（t）的均值不具有各态历经性。

证明略。

该推论是平稳过程均值具有各态历经性的充分条件，它说明当时间间隔充分大时，若状态呈现不相关性，则均值具有各态历经性。

定理13.2.2　设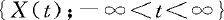是平稳过程，对任意给定的τ，；也是平稳过程，则X（t）的自相关函数具有各态历经性的充要条件是

其中

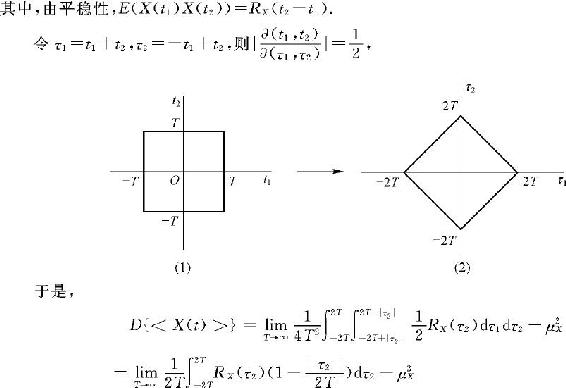
证明：对固定的

故的各态历经性相当于的各态历经性，由于

，由定理13.2.1即得。

实际中讨论的平稳过程为，此时，过程的时间均值为

对于任给的τ，过程的时间相关函数为

相应的各态历经定理与定理13.2.1和定理13.2.2相同。

实际问题中要严格验证平稳过程是否满足各态厉经条件是比较困难的，但各态历经定理的条件较宽，工程中所遇到的平稳过程大多数都能满足。

各态历经定理的重要价值在于从理论上保证一个平稳过程如果是各态历经的，则“以概率1成立”用一条样本函数的时间平均确定出过程的均值和自相关函数。

设试验记录了在时间区间［0，T］上的样本函数x（t），则均值的估计为

自相关函数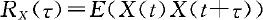的估计为