电阻混联电路

一、混联电路

在实际电路中，既有电阻串联又有电阻并联的电路，称为混联电路。如图3－5－1所示。其中图（a）所示混联电路中，R1、R2、R33个电阻之间的连接关系是：R1与R2先串联，然后再与R3并联。图（b）所示混联电路中，R1、R2、R33个电阻之间的连接关系是：R2与R3先并联，然后再与R1串联。

二、混联电路的一般分析方法

混联电路的一般分析方法如下：

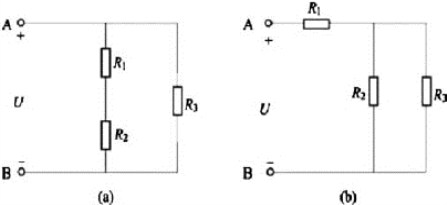
图3－5－1　电阻混联电路

1）求混联电路的等效电阻。先计算各电阻串联和并联的等效电阻，再计算电路总的等效电阻。

2）求混联电路的总电流。由电路的总的等效电阻和电路的端电压计算电路的总电流。

3）求各部分的电压、电流和功率。根据欧姆定律、电阻的串、并联特点和电功率的计算公式分别求出电路各部分的电压、电流和功率。

【例3－5－1】　如图3－5－2所示电路，已知U＝220V，R1＝R4＝10Ω，R2＝300Ω，R3＝600Ω。试求：

（1）电路的等效电阻R；

（2）电路中的总电流I；

（3）电阻R2两端的电压U2；

（4）电阻R3消耗的功率P3。

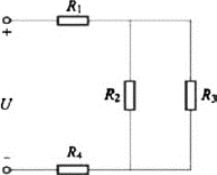
图3－5－2

【解】　（1）电路的等效电阻

（2）电路中的总电流

（3）电阻R2两端的电压

U2＝U－I（R1＋R4）＝（220－1×20）V＝200V

（4）电阻R3消耗的功率

也可用其他方法求解电阻两端的电压U2和电阻R3消耗的功率P3。

三、联电路的等效变换与等效电阻的求法

在实际电路中，有些混联电路往往不易一下子看清各电阻之间的连接关系，这是需要根据电路的具体结构，按照电阻串、并联电路的定义和性质，进行电路的等效变换。混联电路的等效变换通常采用等电位法，等电位法的一般分析方法如下：

（1）确定等电位点，标出相应的符号

导线的电阻和理想电流表的电阻可忽略不计，可以认为导线和电流表连接的两点是等电位点。

（2）画出串、并联关系清晰的等效电路图

根据等电位点，从电路的一端画到另一端，一般先确定电阻最少的支路，再确定电阻次少的支路。

（3）求解等效电阻

根据电阻串、并联的关系求出等效电阻。

【例3－5－2】　如图3－5－3（a）所示电路中，R1＝R2＝R3＝R4＝10Ω，试求S断开与闭合时AB间的等效电阻。

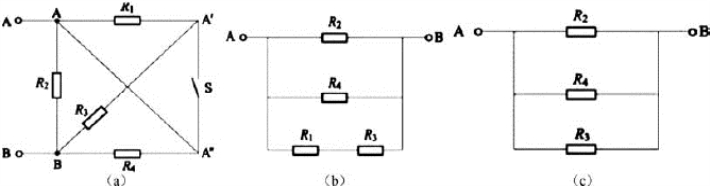
图3－5－3

分析　S断开时，A″A为等电位点；从A点出发到B点有三条通路，第一条通过R2，第二条通过R4，第三条通过R1与R3；其简化等效电路如图（b）所示，即R1与R3串联再与R2、R4并联。S闭合时，A″、A′与A为等电位点；从A点出发到B点仍有三条通路，第一条通过R2，第二条通过R4，第三条通过R3，R1接在A与A？之间，被短路；其简化等效电路如图（c）所示，即R2、R3、R4并联。

【解】　（1）S断开时：

（2）S闭合时：