函数项级数的一致收敛性

§5.2　函数项级数的一致收敛性

通过部分和函数列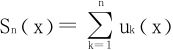的转换，函数项级数的一致收敛性和函数列的一致收敛性就化归于同一个概念。但常常函数项级数的部分和难以求得，故对于函数项级数的一致收敛性，又有一套独特的判别法，即从通项u_n（x）的分析入手。

在对具体的函数列或函数项级数作一致收敛的判定时，明确一致收敛性的内涵是极重要的。

一、一致收敛概念

1．点态收敛复习

设函数列｛S_n（x）｝定义于区间I上，∀x∈I，有，称｛S_n（x）｝在I上点态收敛。

ε-N语言：∀x∈I，∀ε>0，∃N（ε；x），当n>N时，有

｜S_n（x）－S（x）｜<ε

对于函数项级数，点态收敛即为数项级数的收敛性，或将上述S_n（x）理解为部分和即可以，并无什么新的内涵。

2．函数列一致收敛定义

设｛S_n（x）｝和S（x）定义于同一个区间I上，假若∀ε>0，∃N＝N（ε），当n>N时，∀x∈I有

｜S_n（x）－S（x）｜<ε

称｛S_n（x）｝在I上一致收敛于S（x），记成S_n（x）⇒S（x）（n→∞）

注　引入范数，则S_n（x）一致收敛于S（x）可以表示为

3．函数项级数一致收敛定义

若∑u_n（x）的部分和｛S_n（x）｝在I上一致收敛，称∑u_n（x）在I上一致收敛。

注　引入尾项，则∑u_n（x）一致收敛⇔r_n（x）⇒0（x∈I）。针对交错级数∑（－1）^n－1u_n（x），若u_n（x）↘0（n→＋∞），则｜r_n（x）｜≤u_n＋1（x）易处理。

二、不一致收敛的叙述

1．设｛S_n（x）｝在I上点态收敛于S（x）（n→∞）。S_n（x）不一致收敛于S（x）的含义是：∃ε>0，∀N，∃n>N及x_n∈I，st｜S_n（x_n）－S（x_n）｜≥ε₀。

或等价表述为：

2．存在一点列｛x_n｝⊂I，使得

通常在较简单的情形，点列｛x_n｝可以凭直觉尝试确定；而在一般较复杂情形，点列｛x_n｝可取作S_n（x）－S（x）的最大值点。

3．对函数项级数∑u_n（x）而言，不一致收敛可叙述为：

∃ε₀>0，∀N　∃n>N及x_n∈I，

4．简言之，∃｛x_n｝⊂I，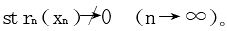

由于牵涉到尾项r_n（x）的估计，除非在特殊场合，一般情形下直接用定义证明函数项级数的不一致收敛是困难的，往往寻求其他途径。

三、一致收敛判别法

S_n（x）可以是给定的函数列，也可以认为是函数项级数的部分和序列。

是极限函数或和函数（假设点态收敛），兹列举常用的一致收敛判别法如下：

2．Cauchy准则

（1）函数列：∀ε>0，∃N，∀n>m>N，∀x∈I有｜S_n（x）－S_m（x）｜<ε；

（2）级　数：∀ε>0，∃N，∀n>N，p＝1，2，…，∀x∈I有

（3）推　论：∑u_n（x）一致收敛的必要条件是　

3．Dini定理

设｛S_n（x）｝，S（x）皆在闭区间［a，b］上连续，S_n（x）→S（x），又∀x∈［a，b］，｛S_n（x）｝单调，则在［a，b］上

级数情形：若函数项级数∑u_n（x）每项u_n（x）在［a，b］上非负、连续且其和函数也在［a，b］上连续，则∑u_n（x）在［a，b］上必一致收敛。

4．设S_n（x）在c点左连续，且｛S_n（c）｝发散，则∀δ>0，｛S_n（x）｝在（c－δ，c）上不一致收敛。

注　1°改为在c点右连续，则｛S_n（x）｝在（c，c＋δ）上不一致收敛；

　　2°级数情形有相应的结论。

5．若S_n（x）→S（x），S_n（x）连续，但S（x）有间断，则S_n（x）不一致收敛S（x）。

6．Weierstrass判别法。

7．乘积项级数的Abel法、Dirichlet法。

例1　证明在［－1，1］上一致收敛。

证法一　此为等比级数，公比q＝1－x²（x≠0时），可从定义出发。

余项

r^′_n（x）＝（1－x²）ⁿ－2x²n（1－x²）^n－1＝（1－x²）^n－1［1－（2n＋1）x²］

得稳定点为±1，

故级数在［－1，1］上一致收敛。

证法二　利用Weierstrass法　u_n（x）＝x³（1－x²）ⁿ　令u′_n（x）＝0

即　（1－x²）^n－1［3－（3＋2n）x²］＝0

得出最大值点为

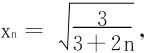
而

证法三　利用Dini定理　S（x）＝x连续，u_n（x）同号（∀x∈［－1，1］）且连续。

例2　判别级数在R上的一致收敛性。

分析　级数在R上处处收敛易判别，且

则

证一　分段技术：｜x｜≤ε和｜x｜>ε两个部分

可见，r_n（x）⇒0（x∈R）。

证二　且非负，于是

而易求得

证三　利用Dirichlet判别法。

注　该级数在R上不绝对一致收敛，但在任何不包含原点的闭区间上却是绝对一致收敛。详细证明请读者补上。

例3　讨论的收敛性及一致收敛性。

解　当｜x｜≤1时，

，级数发散。

当x>1时，收敛，故原级数收敛。

当x<－1时，可取n充分大时

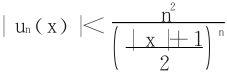
原级数亦收敛。

下面考虑一致收敛性。

在x＝±1处，原级数发散知在（－∞，－1）∪（1，＋∞）上一定不一致收敛，下面证在其上是内闭一致收敛，∀δ>0，先考虑在［1＋δ，∞）上的情形。

当x≥1＋δ时，收敛。

由W－法知，∑u_n（x）在［1＋δ，∞）上一致收敛。再考虑x≤－1－δ时，可取n充分大，使得余下类似。

当然可以合并当｜x｜≥1＋δ时，有（只要n充分大）。

例4　证明在（0，＋∞）上非一致收敛，在任意有限区间上一致收敛（即在（0，∞）内闭一致收敛）。

证一　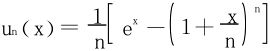，∀x>0，u_n（x）→0，（n→＋∞）

但是u_n（x）不一致收敛于0，因为。或说‖u_n‖_{（0，∞）}＝∞，得知级数在（0，＋∞）上非一致收敛。

在任意有限区间［a，b］，由不等式证明一节§3.7例6知（这是难点所在）：

设｜a｜，｜b｜≤M，则n>M时，有，则，由Weierstrass法知原级数在［a，b］上一致收敛。

注　1．既然原级数在任意有限区间［a，b］上都一致收敛，得知级数在R上处处收敛。

　　2．上述证法应用了§3.7例6的不等式，这是略显牵强的。能否证明得更加“原生态”一点呢？下面我们就作一尝试。

证二　先考虑点态收敛性。引入

所以通项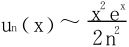。∀x∈R，∑u_n（x）都收敛。

以下再考虑内闭一致收敛性。

先证g_n（x）在（0，＋∞）上递增。

，欲g′n（x）>0，当且仅当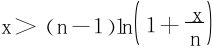，利用ln（1＋t）<t易知此结果成立。现任取M>0，x∈［0，M］，

又，于是n充分大时，有

从而级数∑u_n（x）在［0，M］上一致收敛。

证三　在此我们用尝试法得出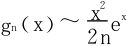。无穷级数∑u_n的敛散性判断关键在于通项u_n无穷小阶的分析。g_n（x）→0（n→∞）显然，但未知是多少阶的无穷小量。尝试如下的极限式：

所以。以下和证法二相同。

例5　若函数φ_n（x）在［a，b］单调，且∑｜φ_n（a）｜，∑｜φ_n（b）｜均收敛，则∑φ_n（x）在［a，b］一致收敛。

证明　因为｜φ_n（x）｜≤max｛｜φ_n（a）｜，｜φ_n（b）｜｝≤｜φ_n（a）｜＋｜φ_n（b）｜

　　　所以由M－判别法知

例6　对任何n，f_n在［a，b］上单调增加，且｛f_n｝收敛于连续函数f，证明

f_n⇒f₀（x∈［a，b］）

证　首先从f_n→f，∀ε>0，∃N＝N（ε；x），当n>N时，

｜f_n（x）－f（x）｜<ε

如何找一个对所有x∈［a，b］都适用的N＝N（ε），使得上式成立呢？

因为f在［a，b］连续，故一致连续，对ε>0，∃δ>0，当｜x′－x″｜<δ时

｜f（x′）－f（x″）｜<ε

取自然数，将［a，b］m等分：

a＝x₀<x₁<x₂<…<x_m＝b

由（0≤k≤m，点态收敛）知，存在一个公共的N，st n>N时，∀k＝0，1，…，m皆有

｜f_n（x_k）－f（x_k）｜<ε

∀x∈［a，b］，设x∈［x_k－1，x_k］，由f_n单调性知

f_n（x_k－1）－f（x）≤f_n（x）－f（x）≤f_n（x_k）－f（x）

而

f_n（x_k）－f（x）＝f_n（x_k）－f（x_k）＋f（x_k）－f（x）<2ε（n>N）

　　f_n（x_k－1）－f（x）＝f_n（x_k－1）－f（x_k－1）＋f（x_k－1）－f（x）>－2ε

所以n>N时有

｜f_n（x）－f（x）｜<2ε（∀x∈［a，b］成立）

例7　（Dini定理）若在有限区间［a，b］上连续函数序列｛S_n（x）｝收敛于连续函数S（x），而对每个x，是单调数列，则S_n（x）在［a，b］上一致收敛于S（x）。

证明　反证法，假设S_n（x）不一致收敛于S（x），则∃ε₀>0，∀N，∃n>N及x₀∈［a，b］，满足

｜S_n（x₀）－S（x₀）｜≥ε₀

于是存在一列正整数n₁<n₂<…，和点列｛x_k｝⊂［a，b］，满足

由Weierstrass定理，｛x_k｝有收敛子列，不妨就设其本身，x_k→ξ∈［a，b］

由S_n（ξ）→S（ξ），得N，使

下面将从（1）（2）式中推出矛盾，由S_n（x），S（x）的连续性，得出

由保号性，∃K，stk>K时，｜S_N（x_k）－S（x_k）｜<ε₀

由｛S_n（x）｝单调趋于S（x）知，n>N时，更有

此与（1）式矛盾，事实上总可以取k>K且n_k≥N同时成立。

例8　假设f（x）∈C（R），且x≠0时，有｜f（x）｜<｜x｜，依递推关系构造如下函数列：f₁（x）＝f（x），f₂（x）＝f（f（x）），…，f_n（x）＝f（f_n－1（x）），证明f_n（x）在［－A，A］上一致收敛（或说：f_n（x）在任何有限区间内一致收敛。）

证明　易推得f（0）＝0，故在R上，｜f（x）｜≤｜x｜等号仅在原点成立。

∀ε>0，当｜x｜≤ε时，｜f（x）｜≤ε

　　　当｜x｜≥ε时

由闭区间上连续函数的最大值定理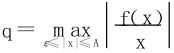，则0<q<1。

在［－A，－ε］∪［ε，A］上，｜f（x）｜≤q｜x｜≤qA。

总之，在［－A，A］上，｜f（x）｜≤max｛ε，qA｝，∀x∈［－A，A］，

若｜f（x）｜≤ε，则｜f₂（x）｜＝｜f（f（x）｜≤｜f（x）｜≤ε；

若｜f（x）｜≥ε，则｜f₂（x）｜≤q｜f（x）｜≤q²A。

总之，｜f₂（x）｜≤max｛ε，q²A｝…

一般地，有｜f_n（x）｜≤max｛ε，qⁿA｝≤ε（n>N时，∀x∈［－A，A］）

注　在R上相应结论未必成立。请举出反例。

例9　设｛f_n（x）｝在［a，b］上满足条件：存在正常数K使得

｜f_n（x）－f_n（y）｜≤K｜x－y｜x，y∈［a，b］，n＝1，2，…

证明　（1）若f_n点态收敛于f，则f_n必一致收敛于f。

　　　（2）若∀x∈［a，b］，｛f_n（x）｝有界，则必有｛f_n（x）｝的子列一致收敛。

分析　（1）∀x∈［a，b］，∃N（ε；x），n，m>N时，｜f_n（x）－f_m（x）｜<ε

注意到｜f_n（x）－f_n（y）｜≤K｜x－y｜的条件，∃δ>0，使N（ε；x）对于U（x₀；δ）内的一切点适用，于是可以选定有限个点x₁，x₂，…，x_p分别确定N（ε；x_i）

（2）由（1）可知，只要证明能选出｛f_n（x）｝的子列，使其在有理点收敛。

证明　（1）∀ε>0，取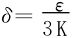，当｜x－y｜<δ时，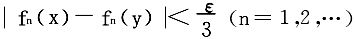

取正整数p，st　，对［a，b］作p等分，x₁<x₂<…<x_p，f_n（x_i）→f（x_i）（i＝0，1，2，…p），因此存在N，当m，n>N时

∀x∈［a，b］，必有i，使x∈U（xi；δ），从而

｜f_n（x）－f_m（x）｜≤｜f_n（x）－f_n（x_i）｜＋｜f_n（x_i）－f_m（x_i）｜＋｜f_m（x_i）－f_m（x）｜<ε

由Cauchy准则，｛f_n（x）｝一致收敛。

（2）设E＝｛x₁，x₂，_…｝为［a，b］的全体有理点，则f_n（x₁）是有界数列，选出收敛子列｛f_n，1（x₁）｝，；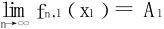

又｛f_n，1（x₂）｝有界，选出子列｛f_n，2（x₂）｝，使得；

…

如此下去，得出子列｛f_n，m（x_m）｝，使得。

考虑对角线序线｛f_n，n（x）｝，对固定的k，｛f_n，n（x_k）｝（n≥k）是｛f_n，k（x_k）｝（n≥k）的子列，故收敛于A_k，因而｛f_n，n（x）｝在E上点态收敛。剩下只要证明：对任一［a，b］上的无理点z，｛f_n，n（z）｝也收敛，只要用（1）中的证明技巧即可。

注1°　设｛f_n（x）｝是区间I上的函数列，若∀ε>0，∃δ>0，使当｜x－y｜<δ时，有

｜f_n（x）－f_n（y）｜<ε（n＝1，2，…）

　　则称｛f_n（x）｝在I上等度连续。本题中的条件｜f_n（x）－f_n（y）｜≤K｜x－y｜可以用等度连续代替，当然等度连续⇒一致连续⇒连续，且极限函数也一定是一致连续的，反之，闭区间上一致收敛的连续函数列必等度连续（见下节例10）。

　2°　证明（2）中的方法，叫做Cantor对角线法。

例10　设函数序列在区间I上定义，满足

i）｜f₀（x）｜≤M；

ii）（∀m＝0，1，2，…，成立）；

iii）数项级数∑b_n收敛。

试证明级数）在I上一致收敛。

分析　题中条件ii）启发我们使用Abel变换，对于乘积项和式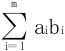，记

B₁＝b₁，B₂＝b₁＋b₂，…，B_m＝b₁＋b₂＋…＋b_m，则b_i＝B_i－B_i－1，代入得　即为Abel变换。再结合Cauchy收敛准则。

证明　依Cauchy收敛准则，欲分析当n充分大时能否充分小。

改记B₁＝b_n＋1，B₂＝b_n＋1＋b_n＋2…，利用Abel变换

因∑b_n收敛，∀ε>0，∃N，n>N，∀p＝1，2，…有

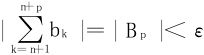
又　

最终得∀ε>0，∃N，n>N时，∀x∈I，有

，证毕。

例11　设级数∑u_n（x）在I上一致收敛，则可以对其适当加括号，使得所得新级数在I上绝对一致收敛。

分析　只涉及级数本身性质，而跟和函数关系不大时，Cauchy准则是首推工具。

证明　因∑u_n（x）在I上一致收敛，∀ε>0，∃N，stn>N，p＝1，2，…时，

特取，∃N₁，st　n>N₁时，∀p＝1，2，…，∀x∈I，有

，∃N₂>N₁，stn>N₂时，∀p＝1，2，…，∀x∈I，有

……

，∃N_j>N_j－1，stn>N_j时，∀p＝1，2，…，∀x∈I，

记则

由W－法知在I上一致收敛，也绝对收敛。

例12　设｛a_n｝是单调减少且趋于零的数列，则级数∑a_n sinnx

（1）在R上处处收敛；

（2）在任何不含2kπ（k∈Z）的闭区间上一致收敛；

（3）^*在任何区间上都一致收敛的充分必要条件是lim na_n＝0。

证明　（1）当x＝2kπ时，原级数通项为0，收敛，现不妨设x∈（0，2π），因

由狄利克雷判别法知∑a_nsinnx在0<x<2π收敛。

（2）等价于证明在（0，2π）内闭一致收敛，∀0<δ<π，在［δ，2π－δ］上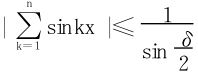，为一致有界，得知在［δ，2π－δ］上一致收敛。

（3）留待读者思考（此问题有相当难度，有兴趣的读者朋友可参阅［9］，［11］）。

习题5.2

1．讨论以下函数列或函数项级数的一致收敛性。

（1）　（i）在任意有限区间　（ii）在R上

（2）

（3）

（4）f₀（x）是［a，b］上的可积函数，在［a，b］上。

2．可微函数序列｛f_n（x）｝在［a，b］上收敛，且∃M>0，使｜f′_n（x）｜≤M，（∀n，∀x∈［a，b］）。试证：｛f_n（x）｝在［a，b］上一致收敛。

3．设f_n（x）在［a，b］可积，一致有界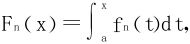，证明｛F_n（x）｝存在子列在［a，b］一致收敛。

4．讨论以下函数项级数的一致收敛性

5．设一元函数f在x＝0的邻域里有二阶连续导数，f（0）＝0，0<f′（0）<1，函数f_n是f的n次复合，证明级数在x＝0的某邻域里一致收敛。

6．证明：若∑u_n（x）在区间I上收敛，则其为一致收敛的充要条件是∀｛x_n｝⊂I，有（其中为级数余和）。

7．设f与f_n在［a，b］连续，如果∀x∈［a，b］，x_n∈［a，b］，只要，就有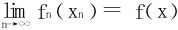，则｛f_n｝在［a，b］上一致收敛于f。

8．设｛f_n（x）｝为［a，b］上连续函数序列，且f_n（x）⇒f（x），x∈［a，b］。

　证明：若f（x）在［a，b］上无零点，则当n充分大时，f_n（x）在［a，b］上也无零点。并有。

（华东师大2000年）

9．设f∈C（R），作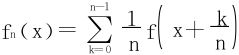。证明｛f_n（x）｝在任何有限区间上一致收敛。

（北师大2002年）

10．设f在［0，1］上连续可导，f（1）＝0。证明函数项级数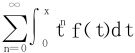在x∈［0，1］上一致收敛。

（北师大2003年）

11．设f∈C［0，1］，令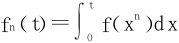，t∈［0，1］，n＝1，2，…，证明函数列｛f_n（t）｝在［0，1］上一致收敛于函数g（t）＝tf（0）。

（中山大学2007年）