静态贝叶斯博弈

为了更好地说明不完全信息与完全信息之间的差异,我们用一个典型静态贝叶斯博弈作为例子,来说明静态贝叶斯博弈概念。

一、不完全信息的古诺模型

考虑如下两寡头进行同时决策的产量竞争模型。其中,市场反需求函数由P(Q)=a-Q给出,这里Q=q1+q2为市场中的总产量。企业1的成本函数为C1(q1)=c1q1,不过,企业2的成本函数以θ概率为C2(q2)=cHq2,以1-θ概率为C2(q2)=cLq2,这里cL<cH,并且信息是不对称的:企业2知道自己的成本函数和企业1的成本函数,企业1知道自己的成本函数,但只知道企业2边际成本为高的概率是θ,边际成本为低的概率是1-θ(企业2可能是新进入这一行业的企业,也可能刚刚发明一项新的生产技术)。上述一切都是共同知识:企业1知道企业2享有信息优势,企业2知道企业1知道自己的信息优势,如此等等。

现在我们来分析这个静态贝叶斯博弈。一般情况下,企业2的边际成本较高时会选择较低的产量,边际成本较低时会选择较高的产量。企业1从自己的角度,会预测企业2根据其成本情况将选择不同的产量。设企业1的最佳产量选择为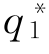,企业2边际成本为cH时的最佳产量选择为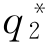(cH),企业2边际成本为cL时的最佳产量选择为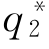(cL),如果企业2的成本较高,它会选择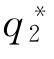(cH)满足:

从而,企业1为了使利润最大化,选择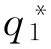应满足:

三个最优化问题的一阶条件为:

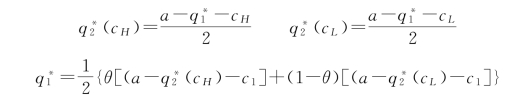
三个一阶条件构成的方程组的解为:

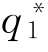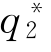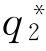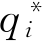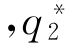把这里的、(cH)和(cL)与成本分别为c1和c2的完全信息的古诺均衡相比较,假定c1和c2的取值可使得两个企业的均衡产量都为正,在完全信息的条件下,企业的产出为=(a-2ci+cj)/3。与之不同的,在不完全信息条件下,当c2=cH,(cH)>;当c2=cL(cL)<。之所以会出现这种情况,是因为企业2不仅根据自己的成本调整其产出,同时还将考虑到企业1的情况选择最优反应。如果企业2的成本较高,它就会因成本较高而减少产量,但同时又会生产稍多一些,因为它知道企业1将根据期望利润最大化的原则决定产出,从而要低于企业1确知企业2成本较高时的产量。

二、静态贝叶斯博弈介绍

现在,我们要建立非完全信息同时行动博弈的标准式表述,也称为静态贝叶斯博弈。首先要表示出非完全信息的关键因素,即每一个博弈方知道自己的收益函数,但也许不能确知其他博弈方的收益函数。令博弈方i可能的收益函数表示为ui(a1,…,an;ti),其中ti称为博弈方i的类型(type),它属于一个可能的类型集[也称为类型空间(type space)]Ti,每一类型ti都对应着博弈方i不同的收益函数的可能情况。

作为具体的例子,考虑前面的古诺博弈。企业的行动使其产量选择q1和q2。企业2有两种可能的成本函数,从而有两种可能的利润或收益函数:

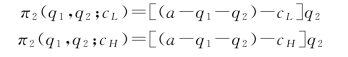
企业1只有一种可能的收益函数:

我们认为企业2的类型空间为T2={cL,cH},企业1的类型空间为T1={c1}。

在这样定义博弈方的类型之后,认为博弈方i知道自己的收益函数也就等同于认为博弈方i知道自己的类型,类似地,认为博弈方i可能不确定其他博弈方的收益函数,也就等同于认为博弈方i不能确定其他博弈方的类型。我们用t-i={t1,…,ti-1,ti,ti+1,…,tn}表示其他博弈方的类型,并用T-i表示t-i所有可能的值的集合,用概率表示博弈方在知道自己的类型是ti的前提下,对其他博弈方类型t-i的推断,即在自己的类型是ti的前提下,对其他博弈方类型t-i出现的条件概率的判断。在完全信息静态博弈标准式的基础上,增加类型和推断两个概念,得到静态贝叶斯博弈的标准式概念。

定义8.1　一个n人静态贝叶斯博弈的标准式表述包括:博弈方的行动空间A1,…,An及其类型空间T1,…,Tn,他们的推断为p1,…,pn,他们的收益函数为u1,…,un。博弈方i的类型作为博弈方i的私人信息,决定了博弈方i的收益函数ui(a1,…,an;ti)。博弈方i的推断描述了i在给定自己的类型ti时,对其他n-1个博弈方可能的类型t-i的不确定性。

我们用

表示这一博弈。

静态贝叶斯博弈的一般表示法,对于由现实问题抽象和建立静态贝叶斯博弈模型提供了思路和帮助,我们根据静态贝叶斯博弈表达式中的几个方面,来确定模型的主要内容。不过,最重要的是用什么样的方法来分析这类博弈呢?