二阶系统的时域响应

式中：ωn为无阻尼自然频率；ζ为阻尼比。系统特性均可用这两个参数加以描述。

二阶系统的特征方程

可得二阶系统的闭环特征方程根（即闭环极点）为

随着阻尼比ζ不同，p1、p2可能为实根或共轭复根。

（2）临界阻尼（ζ＝1）时，p1，2＝－ωn，是二重负实根；

（3）过阻尼（ζ＞1）时，p1，2＝－ζωn±ωn，是两个不相同的负实根；

（4）无阻尼情况（ζ＝0）时，p1，2＝±jωn，是一对纯虚根；

（5）负阻尼（ζ＜0）时，p1，2＝－ζωn±ωn，正实部的共轭复根或至少一个为正实根。

［例3-05］ 如图3-10所示的二阶系统，分别求K＝5及K＝25时的系统无阻尼频率ωn和阻尼比ζ。

图3-10 系统方块图

［解］ 系统的闭环传递函数为

化为标准二阶系统传递函数的形式为

当K＝5时，ωn＝＝3．46rad／s，ζ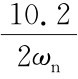＝＝1．47

当K＝25时，ωn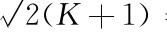＝＝7．21rad／s，ζ＝＝0．707

可以看到增益增大时，ζωn即衰减系数不变，调整时间不变，系统阻尼减小，系统在虚轴上投影变大即振荡频率增大。

［例3-06］ 已知二阶系统G（s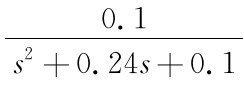）＝，求取系统无阻尼振荡频率、阻尼比、极点。

［解］ MATLAB中程序为

MATLAB运行结果为

因为无阻尼振荡频率、阻尼比、极点仅与分母多项式有关，故程序中damp（sys）也可以改用damp（den）。

2）二阶系统的阶跃响应

在单位阶跃函数作用下（R（s）＝1／s），二阶系统输出

（1）欠阻尼（0＜ζ＜1）时，

其中ωd＝ωn称为阻尼自然频率。

拉氏反变换可得欠阻尼二阶系统单位阶跃响应

或

式中：β＝arctan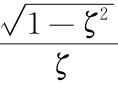，在s平面上的定义如图3-11所示；β角取值仅与阻尼比ζ有关，不同无阻尼自然频率ωn、相同阻尼比ζ的二阶系统的极点有相同的β角，在同一条射线上，此射线名为等ζ线。

图3-11 β角的定义

图3-11也反映了二阶系统闭环极点p1，p2分布及其与β角、无阻尼自然频率ωn、阻尼自然频率ωd、衰减系数ζωn和阻尼比ζ间的关系。欠阻尼二阶系统的单位阶跃响应由稳态分量和瞬态分量组成。瞬态分量是以频率为ωd的阻尼正弦振荡且按ζωn的指数规律衰减，当t→∞时系统不存在稳态误差。ωd值为极点在虚轴上的投影。ζωn在s平面是极点离虚轴的距离，与一阶系统中与虚轴距离一样，可用于表征瞬态分量衰减的快慢，因此二阶系统中衰减系数为ζωn，其值越小，极点离虚轴越近，瞬态分量衰减越慢。

（2）临界阻尼（ζ＝1）时，

将ζ＝1代入式（31）得

拉氏反变换得

临界阻尼的二阶系统阶跃响应由稳态分量和瞬态分量两部分组成。后者随时间增加以衰减系数ζωn按指数律逐渐衰减到零，阶跃响应是单调过程。

（3）过阻尼（ζ＞1）时，

过阻尼二阶系统的极点为

可求得在单位阶跃输入时系统的输出为

可见过阻尼二阶系统的阶跃响应c（t）由三项组成。第一项为稳态分量；第二项和第三项为瞬态分量，它们最终均衰减到零。第三项分量与第二项分量相比，初始值（t＝0）较小，而衰减系数却大许多。因为这项瞬态分量数值小而衰减快，第三项分量可以忽略。故式（33）可近似计算为

式（34）除忽略式（33）中第三项瞬态分量外，还把第二项系数改为1，以避免ζ取值较小的过阻尼系统会略大于1，而使得响应函数c（t）在t＝0时为负值。

（4）无阻尼（ζ＝0）时，

无阻尼二阶系统的闭环极点

p1，2＝±jωn

落在虚轴上，系统处于稳定边界。系统的响应

c（t）＝1－cosωnt （t≥0）

是以频率为ωn的不衰减振荡，故称ωn为无阻尼自然频率。

（5）负阻尼（ζ＜0）时，

如果二阶系统ζ＜0，即负阻尼情况。系统的闭环极点

为具有正实部的共轭复根，或两个实根中至少一个为正实根。其阶跃响应类同上述欠阻尼、临界阻尼、过阻尼，由于ζ＜0，原各式中的指数衰减成分成为指数增长部分，即系统时域响应会发散（见图3-12），系统无法正常工作。后续将不再分析负阻尼情况。

图3-12 负阻尼系统阶跃响应

［例3-07］ 已知二阶系统G（s）＝，绘制ζ分别取值0、0．2、0．4、0．7、1．0、2．0时系统的单位阶跃响应。

［解］ MATLAB程序为

MATLAB运行结果如图3-13所示。其中超调峰点的标记，是在自动产生的阶跃响应曲线窗口的鼠标右键菜单中选择了［CharacteristicsPeak Response］性能指标。

由图3-13可见，临界阻尼及过阻尼时二阶系统的阶跃响应将不出现超调现象。随着阻尼比ζ逐渐减小，系统阶跃响应的振荡程度逐渐增加。在过阻尼系统中以ζ＝1时的瞬态响应时间为最短。在欠阻尼系统中，当ζ＝0．5～0．8时，系统有比较理想的响应曲线，这时瞬态响应时间短，且振荡适度。因此一般希望二阶系统的阻尼比设计在这一范围内。但对于某些情况，如大惯性的温度控制系统等则需要采用过阻尼系统，而对于那些不容许振荡而又要求响应较快的系统，如仪表指示和记录系统，则采用临界阻尼系统。

3）二阶系统的脉冲响应

输入信号为单位脉冲函数（R（s）＝1）时，二阶系统的输出

图3-13 MATLAB运行结果

（1）欠阻尼（0＜ζ＜1）时，上式的拉氏反变换即为二阶系统的脉冲响应

（2）临界阻尼（ζ＝1）时，系统的脉冲响应

（3）过阻尼（ζ＞1）时，系统的脉冲响应

［例3-08］ 已知二阶系统G（s）＝，绘制ζ分别取值0．1、0．25、0．5、1．0时系统的单位脉冲响应。

［解］ MATLAB程序为对应有程序

MATLAB运行结果如图3-14所示。

图3-14 MATLAB运行结果

4）二阶系统的斜坡响应

当输入信号为单位斜坡函数（R（s）＝1／s2）时，系统的输出为

欠阻尼（0＜ζ＜1）时，

临界阻尼（ζ＝1）时，

过阻尼（ζ＞1）时，

MATLAB没有专门的斜坡响应函数，可以采用任意输入的lsim（）函数，也可以将输出信号Y（s）＝G（s）U（s）＝G（s）另写成Y（s）＝［G（s，即对G（s）调用求取单位阶跃响应的step（）函数。