酸碱溶液的

酸碱反应的实质是质子的转移。因此，可根据共轭酸碱对之间的质子转移的平衡关系式来计算溶液中的H＋浓度。具体方法是：列出溶液中酸碱物质的质子条件式，代入有关酸碱平衡常数和浓度的数据，得出计算H＋浓度的精确式，然后在运算过程中根据具体情况进行合理的近似处理，即可得到H＋浓度的近似式及最简式。下面简要介绍各类酸、碱溶液的p H计算方法。

4．2．1 一元酸（碱）溶液的p H计算

1．强酸 （碱）溶液的p H计算

强酸、强碱在溶液中全部离解，在一般条件下，p H计算比较简单。

一元强酸HA（设浓度为camol／L）的质子条件式为：

强酸在溶液中完全离解，则 ［A－］＝ca，代入质子条件式得：

解此一元二次方程得：

上式是计算一元强酸溶液中H＋浓度的精确式。

根据具体情况进行合理的近似处理。若ca≥20［OH－］，水的离解可忽略，则有：

对于强碱也可采用同样方法处理，得：

2．弱酸 （碱）溶液的p H计算

一元弱酸HA（设浓度为camol／L）的质子条件式与一元强酸相同，即：

利用平衡常数式将上式中各项写成 ［H＋］的函数，则有：

由 ［HA］的分布系数得：

代入式 （4－3）得一元三次方程，即得到计算一元弱酸溶液H＋浓度的精确式。此式的数学处理十分麻烦，在实际工作中没有必要精确求解。

若caKa≥20Kw，可忽略式 （4－3）中的Kw。根据离解平衡原理，［HA］＝ca－［H＋］，将其代入得：

这是计算一元弱酸溶液H＋浓度的近似式。

若caKa＜20Kw，但ca／Ka＞500时，酸的离解可忽略，但Kw不能忽略，由式 （4－3）得：

这也是计算一元弱酸溶液H＋浓度的近似式。

若caKa≥20Kw，且ca／Ka≥500时，弱酸离解对总浓度ca的影响也可略去，即［HA］＝ca－ ［H＋］≈ca。因此可得：

这是计算一元弱酸溶液H＋浓度的最简式。实际上，它也是计算一元弱酸p H最常用的公式。

同理，一元弱碱可采用类似方法处理，得到计算OH－浓度的最简式：

【例4－1】计算0．10 mol／L HF溶液的p H。（Ka＝6．3×10－4）

解：用条件式判断：caKa＞20Kw，ca／Ka＜500，用式 （4－4）近似式计算：

则p H＝2．12。

【例4－2】计算0．10 mol／L NH4Cl溶液的p H。

解：此为一元弱酸 （NH4＋）的水溶液，Ka＝5．6×10－10。用条件式判断：caKa＞20Kw，ca／Ka＞500；可用最简式计算：

则p H＝5．12。

4．2．2 多元酸（碱）溶液的p H计算

多元酸 （碱）在溶液中逐级离解，溶液是一个复杂的酸碱平衡体系。以二元弱酸（H2A）为例，设其浓度为camol／L，离解常数分别为Ka1和Ka2。质子条件式为：

［H＋］＝ ［HA－］＋2［A2－］＋ ［OH－］

将有关平衡常数代入，可得：

整理后得计算 ［H＋］的精确式：

若caKa1＞20Kw，上式中Kw项可忽略。

上式是计算二元弱酸溶液中H＋浓度的近似式，实际上是忽略了二级离解，将二元弱酸按一元弱酸处理。一般对于多元弱酸，只要浓度不太小，各步离解常数差别不太小，均可按一元弱酸处理。

与一元弱酸相似，若ca／Ka≥500，则ca－ ［H＋］≈ca，得到计算二元弱酸溶液中H＋浓度的最简式：

【例4－3】计算0．10 mol／L Na2C2O4溶液的p H。

因cbKb1＞20Kw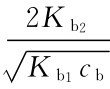， ＜0．05，cb／Kb1＞500，所以用最简式计算：

则p OH＝5．58，p H＝14．00－5．58＝8．42。

4．2．3 两性物质溶液的p H计算

两性物质 （amphoteric substance）在溶液中有两种离解方式，既可得到质子又可失去质子。两性物质溶液中的酸碱平衡较复杂，计算时应根据具体情况进行近似处理。

1．两性物质溶液

两性物质溶液 （HB）的离解：

两性物质溶液质子条件式为：

［H＋］＋ ［H2B＋］＝ ［B－］＋ ［OH－］

将有关平衡常数代入，整理得精确式：

两性物质的Ka1与Ka2均较小，此时可忽略HB的酸式离解和碱式离解，即 ［HB］≈c，代入上式得计算H＋浓度的近似式：

若c Ka2≥20Kw，忽略水的离解；若c≥20Ka1，Ka1＋c≈c，得计算两性物质溶液的最简式：

两性物质的组成不同，涉及的离解平衡式不同，代入的常数也不同。

【例4－4】计算0．01 mol／L邻苯二甲酸氢钾溶液的p H。

解：邻苯二甲酸氢钾的Ka1＝1．1×10－3，Ka2＝3．7×10－6。由于c＞20Ka1，c Ka2≥20Kw，可用最简式［H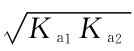＋］＝计算：

则p H＝4．20。

【例4－5】计算0．1 mol／L氨基乙酸 （NH2CH2COOH）溶液的p H。

解：在水溶液中，氨基乙酸 （双极离子）的离解平衡为：

因浓度较大，即c Ka2＞20Kw，c＞20Ka1，可采用最简式计算：

则p H＝6．06。

2．弱酸弱碱混合溶液

弱酸弱碱混合溶液中p H计算式类似于两性物质溶液。

若溶液中同时有弱酸 （NH4Cl）与弱碱 （Na Ac）的混合溶液时，在水中的质子条件式为：

［H＋］＋ ［HAc］＝ ［NH3］＋ ［OH－］

将NH4＋的离解常数K′a，HAc的离解常数Ka代入式 （4－11），则近似式为：

若c NH＋4K′a≫Kw，可忽略分子中的Kw；若c HAc／Ka≫l，可忽略分母中的1，这表明弱酸与弱碱的反应倾向很小，可用各自的分析浓度代替平衡浓度进行计算：

若c Ac－≈c NH＋4，则弱酸弱碱混合溶液H＋浓度的计算可简化为：

【例4－6】计算含0．1 mol／L NH4Cl与0．1 mol／L Na Ac的混合溶液的p H。

解：HAc的离解常数分别为：

因为c NH＋4K′a≫Kw，c HAc／K′a≫1，c Ac－≈c NH＋4，故用式 （4－15）计算：

则p H＝7．01。

4．2．4 缓冲溶液的p H计算

缓冲溶液 （buffer solution）是一种能对溶液的酸度起稳定作用的溶液。在缓冲溶液中加入少量的酸或碱，或因溶液中发生化学反应产生少量的酸或碱，或将溶液稍加稀释而溶液的酸度不发生显著性变化。

常用的缓冲溶液 （表4－1）是弱酸及其共轭碱或弱碱及其共轭酸、高浓度的强酸或强碱、两性物质等组成的溶液。

表4－1 常用缓冲溶液

注：Tris——三 （羟甲基）氨基甲烷，一般不抑制酶活性，为生物和临床测量中常用的缓冲溶液。

标准缓冲溶液的p H是由精确的实验测定的。作为一般控制酸度用的缓冲溶液，因为缓冲剂本身的浓度较大，对计算结果也不要求十分准确，可以采用近似方法进行计算。

现讨论弱酸 （HA浓度为camol／L）与其共轭碱 （A－浓度为cbmol／L）组成的缓冲溶液。溶液中 ［A－］来自两部分：一是弱酸 （HA）的离解，二是共轭碱 （A－）本身，由于溶液中的A－并未提供质子，因此质子条件式为：

［H＋］＝ ［OH－］＋ （［A－］－cb）

整理得：［A－］＝cb＋ ［H＋］－［OH－］

由质量平衡式得： ca＋cb＝ ［HA］＋ ［A－］

合并两式得： ［HA］＝ca－［H＋］＋ ［OH－］

由弱酸离解常数得到计算缓冲溶液H＋浓度的精确式：

当溶液呈酸性 （p H＜7）时可忽略 ［OH－］，上式简化为近似式：

若酸、碱分析浓度较大，即ca≥20［H＋］，cb≥20［H＋］时，得Henderson缓冲公式：

同理，若溶液呈碱性 （p H＞7）可忽略 ［H＋］；若ca≥20［OH－］，cb≥20 ［OH－］，也可得到上式。

【例4－7】0．30 mol／L吡啶溶液与0．10 mol／L HCl溶液等体积混合，计算此溶液的p H。

解：

等体积混合后，生成C5H5NH＋的浓度为：

则剩余的吡啶浓度为：

吡啶的Kb＝1．7×10－9，Ka＝Kw／Kb，因此，吡啶与吡啶盐组成缓冲溶液，计算得：