等差数列教学设计

等差数列教学设计

张　弓

【课　型】一轮复习课

【三维目标】

1.知识与技能：理解等差数列的概念并能解决简单的实际问题；掌握等差数列的通项公式、前n项和公式，体会等差数列与一次函数、二次函数的关系,提升化归能力及分析问题、解决问题的能力。

2.过程与方法：引导学生系统梳理知识点,建立课时知识体系；通过重点讲解与强化练习，使学生内化知识，提高解题能力，发展思维。

3.情感态度与价值观：激发学生积极思考，发展学生思维的深刻性及数学应用意识和创新意识。

【教学重难点】等差数列的常用性质、通项公式、前n项和公式及其方程思想。

突破措施：深刻理解等差数列的定义及其等价形式,熟练运用通项公式、前n项和公式,注意用函数的观点，方程（组）、消元、整体、数形结合、分类讨论等数学思想分析问题和解决问题。

【高考命题规律及趋势】等差数列为必考内容。题型既有选择题和填空题,又有解答题；难度既有容易题、中等题,也有难题。客观题突出“小而巧”，主要考察性质的灵活运用及对概念的理解，主观题或是较为简单的方程问题，或是“大而全”，着重考察函数方程、等价转化、分类讨论等重要数学思想。

【教学设计过程】

一、高考主体内容、重点、难点及思想方法、命题趋势分析（教师）

二、课时知识体系建构（教师、学生）

1.等差数列的概念：若数列{a_n}从第二项起，每一项与它的前一项的差等于同一个常数，则数列{a_n}叫等差数列，这个常数叫该等差数列的公差（d）。

2.通项公式：a_n=a₁+（n－1）d（公式的推导用了什么方法？）

推广：a_n=a_m+（n－m）d

变式：a₁=a_n－（n－1）d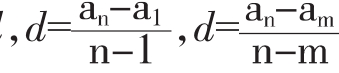（由此联想点列（n，a_n）所在直线的斜率）

3.等差中项：若a、b、c成等差数列，则b称a与c的等差中项，且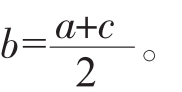

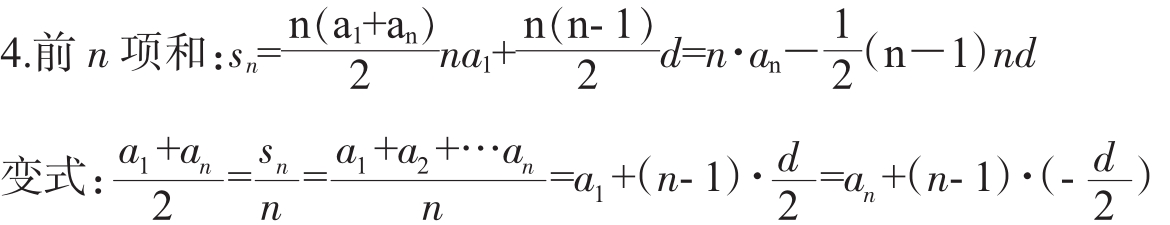
归纳出定性分析等差数列的几个途径：

如：（1）知s_n=n²+3n+1，问｛a_n｝是否为等差数列？它有何特点？

例1：已知数列｛a_n｝满足a_n+2s_ns_n-1=0（n≥2），a₁=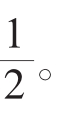

（1）求证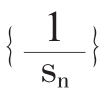为等差数列；

（2）求a_n。

（学生讨论完成,教师总结）此题应抓住条件等式特点，从寻求s_n与s_n-1关系入手；基本工具是s_n与a_n的关系。

5.简单性质及结论：

（1）有穷等差数列的逆向数列依旧是等差数列（见变式）；

（2）等间隔（即序号成等差数列）抽取的子列依旧是等差数列；

如：a_m，a^m+k，a_m+2k，…是以？为公差的等差数列，特别的，｛a_2n｝、｛a_2n-1｝是以2d为公差的子列。

试分析数列｛a_3n-1｝的特点。

（3）若{a_n}、｛b_n｝是两个等差数列，则{ka_n+lb_n}依旧是等差数列；

（4）若m+n=p+q（m，n，p，q∈N₊），则a_m+a_n=a_p+a_q；

特别的：

①到有穷等差数列首末两项距离相等的两项的总和相等；

②m+n=2p时，2a_p=a_m+a_n。

如：s_n=18，s₃=1，a_n+a_n-1+a_n-2=3，则n=?

（5）s_m，s_2m-s_m，s_3m-s_2m，…，构成以m²d为公差的等差数列；

如：s₂=2，s₄=10，则s₆=？上述结论可否推广？

（6）项数为2n（n∈N₊）时，s_偶-s_奇=nd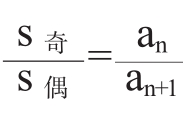，，项数为2n-1（n∈N₊）时，s_偶-s_奇=-a_n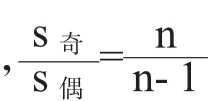，s_2n-1=（2n-1）a_n（由此思考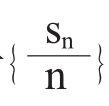和｛a_n｝的关系）；

（8）单调性和s_n的最值：

一般从哪个角度讨论？（利用s_n=f（n））

①d＞0时，a_n，s_n有最小值。

若a₁≥0，则s₁最小；若a₁＜0，则由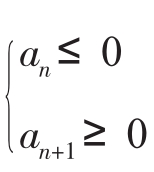确定s_n的最小值。

②d＜0时，a_n，s_n有最大值。

若a₁≤0，则s₁最大；若a₁＞0，则由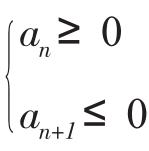确定s_n的最大值。

②d=0时，｛a_n｝为常数列，无严格的单调性。

如：知a_n=-2n+18,试讨论s_n的最值。

三、练习反馈（课前提供题目给学生）

例2：（1）非零实数a，b，c成等差数列，则函数f（x）=ax²+2bx+c的零点个数为_______。

以下问题中，｛a_n｝为等差数列：

（2）若a₁₀=30，a₂₀=50，则a_n=________，又若s_n=242，则n=__________。

（3）公差为正数，若a₁+a₂+a₃=15，a₁a₂a₃=80，则a₁₁+a₁₂+a₁₃=_________。

（4）若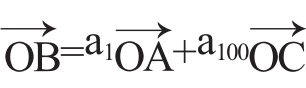，且A，B，C三点共线（该直线不过点O），则s₁₀₀=____________。

（5）数列｛a_n｝共有2n+1项，其中奇数项的和为80，偶数项的和为72，则其项数为____________。

（6）若s_n=20，=38，则=s_3n________________。

（7）｛aⁿ｝、｛bⁿ｝是两个等差数列，s_n、t_n分别为它们的前n项和，若=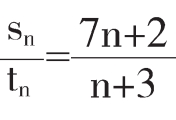，则=___________________。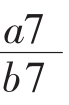

（8）若a₂+a₆+a₁₆=a，则｛s_n｝中可以确定的项是_________________。

（9）200根圆柱形钢管，堆成一三角形垛或梯形垛，每上一层少一根。最下一层最少要放______________根。

（10）｛a_n｝的最大项为1，最小项为，其公差d∈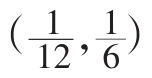，则n的取值的集合为_______________________。。

例3：等差数列｛a_n｝中，a₁=25，s₁₇=s₉。（1）求s_n的最大值；（2）求a₁+a₂+…+a_n。

例4：已知函数f（x）=a₀+a₁x+a₂x²+…+a_nxⁿ（n∈N₊），且函数f（x）的图象经过点（1，n²），数列｛a_n｝为等差数列。

（1）求数列｛a_n｝的通项公式。

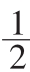（2）当n为奇数时，设g（x）=［f（x）-f（-x）］，是否存在整数m，M，使m＜g（）＜M恒成立？若存在，求出M-m的最小值；若不存在，说明理由。

（此问教师辅导完成）

四、小结（从重点内容、解题思想、技巧方法三个方面让学生完成）

【课后反思】数列部分的两类基本问题：定性分析和定量计算，宜注重概念和基本性质的理解和运用，注重基本量方法。