数学物理模型的建立

二、数学物理模型的建立

(一)蓄冰物理模型

如图1的蓄冰桶，铜管长300mm，外径为16mm，壁厚为1mm。铜管中通入－7℃的乙二醇溶液，冷媒通过管壁与管外的初始温度为15℃水或者水和金属丝(铝丝)的混合体进行热交换，使得水结冰。由于铜管较短，管中的乙二醇溶液在入口和出口温度差基本可以忽略不计，蓄冰桶内乙二醇溶液流动方向温度分布和结冰形状基本都是一致的。所以我们在铜管中心处垂直于乙二醇流动方向截取一个平面如图2所示，以这个平面上的蓄冷工况变化分析整个蓄冰桶内的加丝系统相比于不加丝系统的变化。

(二)数学描述

在实际情况中，由于水存在过冷度，所以即使当水的温度降到凝固点也不会结冰。同时因为金属丝的传热性能远远优于水和冰，所以在金属丝和水之间也会存在着换热。因此，进行数值模拟需对实际问题进行假设，使得问题简单化。现作如下假设:(1)乙二醇进出口温度相同恒为－7℃;(2)蓄冰桶的保温良好，认为其向周围环境散热忽略不计;(3)蓄冰桶内初始水温均匀一致;(4)因为铜管比较薄，忽略铜管的传热热阻和蓄热性能;(5)各项物性参数除了浮力项中的密度外都为常数;(6)金属丝缠绕均匀，多孔介质各向同性;(7)任意一点金属丝与其周围接触的水接触良好，认为没有传热温差;(8)忽略由温度变化引起的金属丝体积变化;(9)在结冰过程中，不存在过冷度，即水温达到0℃水开始结冰。

图1　直角坐标模型示意图

图2　极坐标模型示意图

由以上假设我们可以把结冰区域考虑为多孔介质区域对水平缠丝管蓄冰过程水和丝的传热过程列出方程，考虑到多孔介质作为一个多相介质，用微分方程不能全面地反映介质内部固体骨架和流体的传热传质过程。所以我们在多孔介质中取一个代表性单元体(REV)来作为代表整个多孔介质的控制体。

1．连续性方程。

式中:ε^*为代表性单位体的孔隙率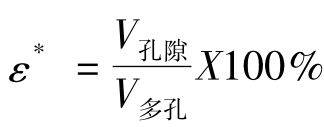;ρ_f为流体密度;[]φ为相平均速度。

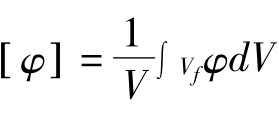2．动量方程

式中:ρ_fF为质量力，在本模型中仅体现为重力;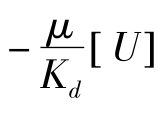为黏性阻力项，即达西项;其中μ为流体动力黏度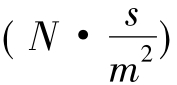

，K_d为多孔介质渗透率;－C_F为针对Re数较大的内部流动的多孔介质达西Forchheimer修正项，C_F为无量纲阻力常数。

根据固体骨架金属丝的特性，把多孔介质考虑为纤维多孔介质，Drummond＆Tahir假设纤维都是直线状的(弯曲度为零)，按方框格子均匀堆积，流体垂直或者平行流过纤维方向得到下列方程:

式中φ为多孔介质固相体积分数，a为纤维直径。在实际生活中，纤维都是会或多或少有一些弯曲，所以DAVIS等对纤维是完全弯曲(弯曲度为100%)做了一系列计算，得到下列加权表格。

表1　纤维弯曲度的加权表

实验测得实验测量金属丝孔隙率为0．9732，即在实验中固体骨架的体积分数为0．0268，代入式(4)中得到k/a²=9．75。利用表1经过加权计算得出k/a²=9．31。

C_F的计算选择Fand等人对Ergun公式中的两个系数进行了优化后的公式。

表2　Ergun公式的优化

根据上式公式，我们假设管壁结冰后与水接触的冰面温度为－1℃，水温为1℃，计算得出Ra=Gr*Pr=1．28X10⁵，根据表6－5确定管外流动为层流。取A=182，B=1．92，代入ε=0．9732，得到C_F=0．148。

3．能量方程。能量方程的表达在冻结区和非冻结区不同，冻结区的方程为方程(6)

非冻结区的方程为方程(7)

式中:下标f表示流体(水)，下标s表示固体骨架。

4．边界条件和初始条件。把铜管当做一个恒定－7℃壁温的边界来看待。假设蓄冰桶体与外界接触壁面保温层保温良好，蓄冰桶与外界换热热流密度为零。

式中:r=R0表示管壁面坐标;r=R1表示蓄冰桶外壁面坐标。

计算区域内的初始温度为15℃。

Tt=0=15℃　　　(10)

为了观察结冰过程中温度各点的温度分布，在蓄冰桶中心竖直方向布置了六个点，0点位冷媒管的位置，1～3点布置在冷媒管的上方，1点距管壁5mm，2点距管壁15mm，3点距管壁25mm，4～6点布置在冷媒管下方，相对于1～3点关于x轴对称。

图3　温度测点示意图