市场预测方法简介

第三节　市场预测方法简介

市场预测是对未来市场情况所做的定量预计，只要预计结论准确，就可据此制定市场营销策略，进行经营管理决策。在科学的市场预测结论基础上开展市场营销活动，可以做到减少失误，获得最佳经济效益。在发达的市场经济条件下，谁能掌握科学的市场预测方法，得到科学的预测结论，谁就能掌握市场的主动权，立于不败之地。

市场预测的内容比市场调研内容要少，偏重于可以定量分析的指标，主要有市场需求预测、市场占有率预测、资源预测、市场价格预测、目标市场预测、技术发展预测等。

在进行市场预测时，预测方法的选择很重要，同样的市场历史资料，预测方法越先进、越科学，预测结论也就越准确、越可靠。

目前，从国外市场营销学说的发展状况看，市场预测方法很多，且新的方法在不断产生，其科学性、准确性也在不断提高。

一、市场预测方法的分类

市场预测方法很多，可以从不同角度划分。从时间上看，有近期预测、中期预测和长期预测。

从预测结论的量化上看，有定性预测法和定量预测法。

（一）定性预测法

定性预测法又叫经验判断法。它是依靠人的经验，对市场未来状况做出判断。该方法预测的主体是有市场经验的人，靠这些人的知识、经验、分析判断能力，在已掌握市场资料的基础上进行主观预测。

这种方法的优点是简便易行，但无定量结论，易受人的主观意志影响。定性预测法从参与人员上分，有专家意见法，销售人员法，用户意见法，领导人员判断法等。

专家意见法：专家意见法是指由市场方面的专家进行有关预测，具体来说，就是请多个有经验的市场专家，对需要预测的市场问题做出回答。在回答问题时，各专家互相不通气，以免互相影响。有时，同一市场预测问题，可在初次意见综合后，反馈给各专家，由他们再次判别，以提高预测结论的兼容性、准确性。

用户意见法：用户意见法是通过走访调查用户，按用户的意见对未来市场情况做出判断。这种方法对于用户数量少，每户用量大的情况更为适用。

销售人员估计法：销售人员估计法是由企业长期从事销售的人员对市场未来供求情况进行估计。此种方法其实是建立在销售人员市场营销经验的基础上，由这些人员根据已经掌握的市场资料而做出预测。显然，这种方法既有主观经验，也有客观依据，因而较为可靠。

领导人员判断法：领导人员判断法是指由企业主要领导者（如厂长、经理）对市场进行预测判断。主要领导在判断前，需要召集有关人员（各业务部门负责人）进行讨论，在广泛听取大家意见的基础上做出自己的判断。

（二）定量预测法

这种方法是根据已有的统计资料，运用各种专门方法（主要是数学方法），对市场未来情况做出定量化的预测。其预测结论的优劣，取决于已有资料的完整性和真实性，也取决于预测方法的科学性。

目前定量预测方法大体上可分为两类：一是传统预测法，这类方法计算过程简单，计算结论可靠性比较差；二是数学模型法，其数学理论较深，计算复杂，但预测结论质量较高。

二、传统预测方法

（一）移动平均法

式中，Y——表示预测值；

　y_t-i——分别表示预测期以前各期的实际数。

（二）加权移动平均法

式中，Y，y_t-i——含义与移动平均法相同。

（三）相关比率推算法

相关比率推算法是先选定某一与目标市场有关的指标，并确定该指标与预测指标之间的数量关系，进而推断出所需的市场预测指标。

例如，我国某年国民生产总值10562亿元，比上年增长5.2%。煤炭总消费量101544万吨，比上年增长1.9%。当年煤炭消费弹性系数为1.9%／5.2%=0.37。若其后5年间国民经济发展总速度为145%，那么相应的第五年煤炭需求量为：

（45%×0.37+1）×101544=118451（万吨）即按相关比率推算第五年煤炭总消费量为11.845亿吨。

（四）指数平滑法

Y_t+1=α×y_t+（1-α）×Y_t

式中，Y_t+1——下期预测值；

　α——平滑系数，取值在0.1～0.9之间；

　y_t——本期实际值；

　Y_t——本期预测值。

例如，某市场2012年煤炭销售量2000万吨，预测销售量为1800万吨，平滑系数选0.6。预测2013年该市场煤炭销售量为：

Y_t+1=α×y_t+（1-α）×Y_t

Y_1a=0.6×2000+（1-0.6）×1800=1920（万吨）

（五）传统定量预测法的评价

上述几种传统预测法的缺陷十分明显，它们不能很好地反映现象增长或减少的变化趋势。当现象增长趋势显著时，预测值往往偏低；反之，在减少趋势下，预测值必然偏高。总之，这些方法预测结论的可靠性、准确性都较差。

三、数学模型预测法

现代市场预测中，传统预测方法逐渐被淘汰，代之以崭新的数学模型预测法。后者无论从方法的科学性上，还是结论的准确性上都有显著提高。数学模型预测法很多，有的要用到较深的数学知识，不易掌握。常用的，便于掌握的数学模型有以下几种方法。

（一）直线回归预测模型

直线回归预测模型是根据现象之间发展变化的直线趋势，拟合一条直线方程，用该直线方程来预测未来数据。所拟合的直线必须满足：直线上数值与实际值离差的平方和为最小。

1.一元线性回归

当现象具有明显增长（或减少）趋势，且逐期增长（或减少）量接近于常数时，可用此种方法。

这种方法的数学表达式为：

Y=a+bx

式中，x——时间；

　Y——需要预测的指标。

对应的时间序列如下：

（时间）x：x₁、x₂、x₃，……，x_n

（指标）y：y₁、y₂、y₃，……，y_n

依上述数值可绘出坐标图（图2-1）（增长趋势）。

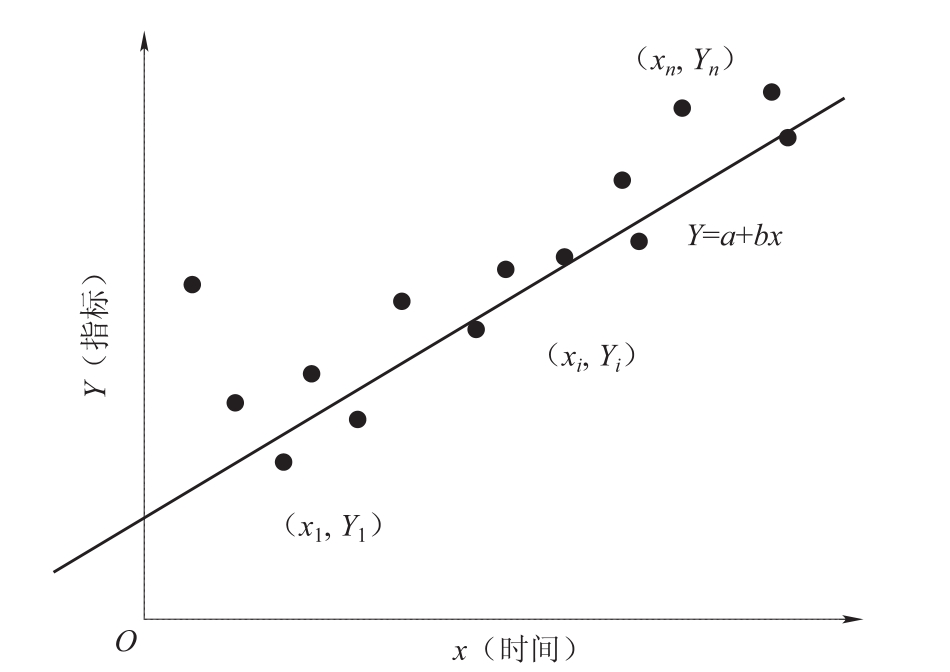
图2.1　直线增长趋势图（时间）

由图2-1，可知，在各散点之间可以拟合一条直线：Y=a+bx；这条直线应界于各散点之内，才可以很好地表达现象的发展变化趋势。

直线拟合中，直线上的点与各实际点之间有偏差，要设法使这些偏差在总体上最小。

因此，拟合直线标准就是：偏差之平方和为最小。

即：∑（y_i-y_i）²达到最小。

由此可得：

f=∑（y_i-a-bx_i）²为最小，其中a，b为自变量。求导数有：

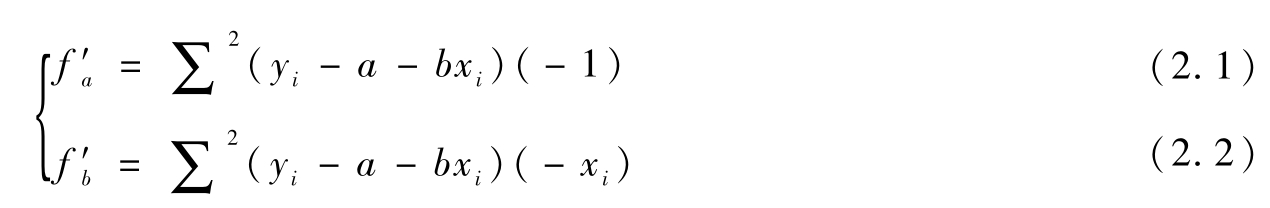
令这两个偏导数为零，上述离差的平方和才会最小。即：

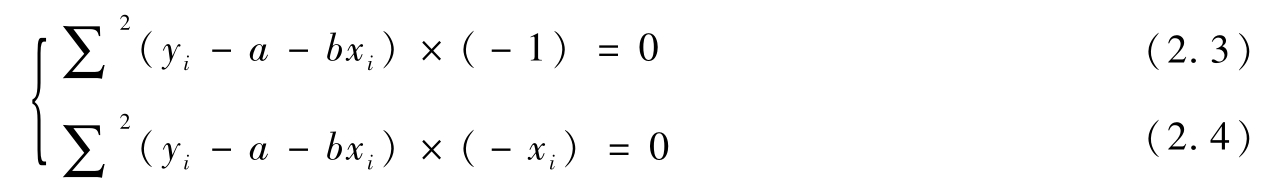
整理得：

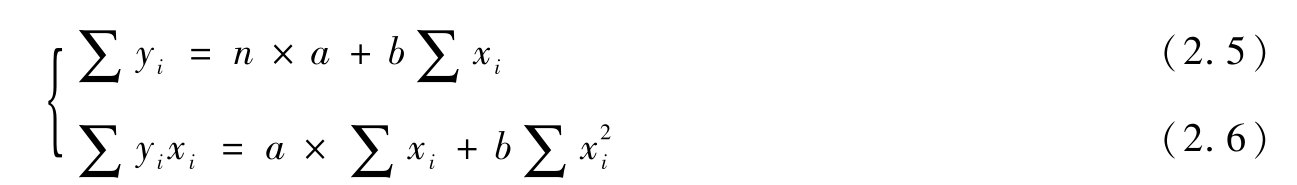
利用此方程组可以求得a，b数值，从而找到这条最合适的直线：

Y=a+bx其中：

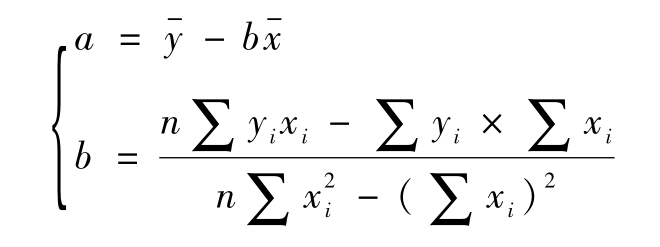
举例如下：

时间x：2008、2009、2010、2011、2012；

原煤销售量（万吨）y：8、10、10、12、14。

依上述资料列表计算，见表2-1：

表2－1　一元线性回归数值计算表

将表2-1数字代入方程组（2.5）、（2.6）有：

求解该方程组，可以求得：

或直接用公式计算：

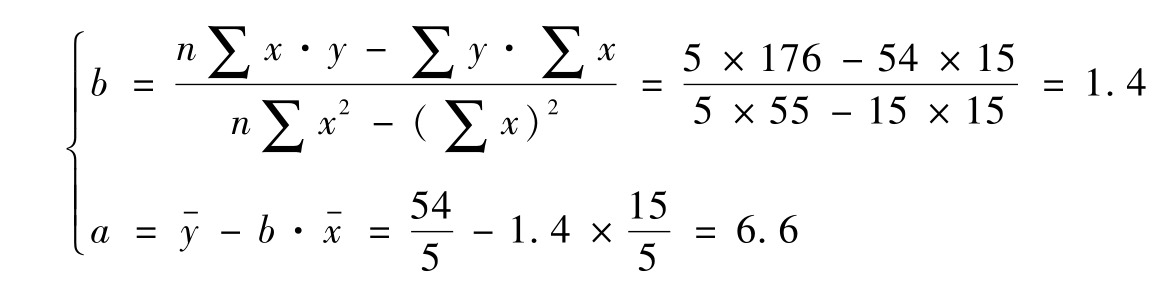
参数a、b求出后，就可以得到相应的直线方程如下：

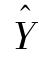=a+bx=6.6+1.4x

预测2013年、2014年销售量为：

Y₁₃=6.6+1.4×6=15（万吨）

Y₁₄=6.6+1.4×7=16.4（万吨）

2.多元线性回归预测

多元线性回归中，影响预测对象的因素已远不止“时间”一个，还有许多其他因素。分别设为X₁、X₂……X_k，这时拟合的直线方程为：

Y=a+b₁x₁+b₂x₂+b₃x₃+b₄x₄+……+b_nx_n

其拟合标准仍是：实际值与趋势值之间离差的平方和为最小。

由此可得到求解a、b等参数的方程组如下：

式中：

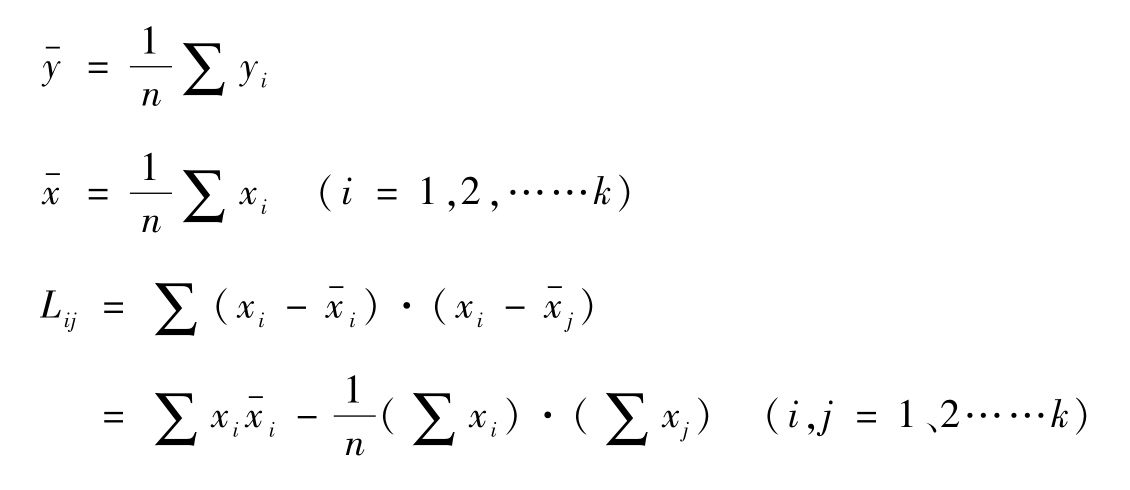
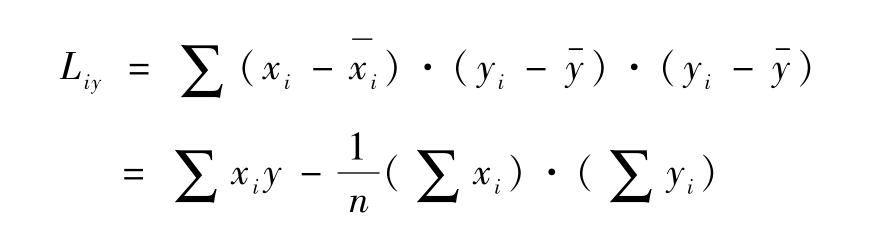
解上述方程组，就可求得参数a、b₁、b₂、……、b_n；

回归方程y=a+b₁x₁+b₂x₂+b₃x₃+b₄x₄+……+b_nx_n也就求出来了。这时只要代入各数值，完全可以预测出对应的预测值。

3.线性回归模型的可信度分析

线性回归方程的可靠程度，可用现象之间的相关系数予以描述，当相关系数的绝对值接近于“1”时，方程可信度高，反之相关系数绝对值接近于“0”，则方程可信度很低。一般来说，相关系数绝对值在0.67以上时，线性回归模型就是基本可信的，尤其是相关系数绝对值在0.9以上时，线性回归模型就是可信的，据此进行的预测，其结论就是可信的。

相关系数计算公式如下：

一元线性回归下：

多元线性回归下：

其中：

现依一元回归中的例题，计算相关系数如下：

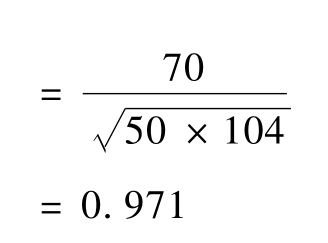
依据所提供数据计算的相关系数：R=0.971；｜R｜非常接近于1，说明所拟合的一元线性回归方程y=a+bx=6.6+1.4x有极高的可信度，完全可以用于市场预测。

（二）曲线回归分析模型

当现象发展变化的趋势不是直线型，而是某种曲线型时，可考虑拟合曲线回归模型。常用的有二次曲线和指数曲线两种。

1.二次曲线（抛物线）

在配置y=ax²+bx+c的抛物线模型时，把x²、x分别看做不同的变量，就可变为多元线性回归的形式，其求解a、b、c三个参数的方程组为：

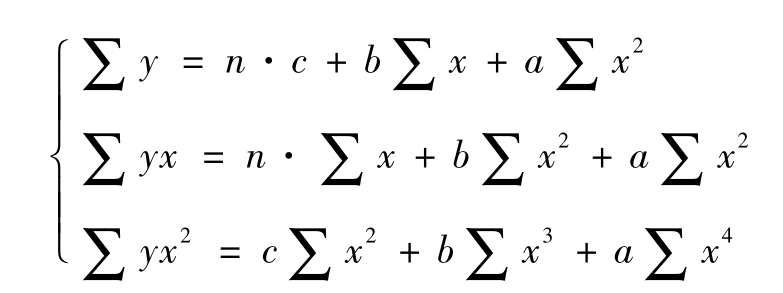
由该方程组就可求出a、b、c三个参数，从而找到回归抛物线模型：

y=ax²+bx+c

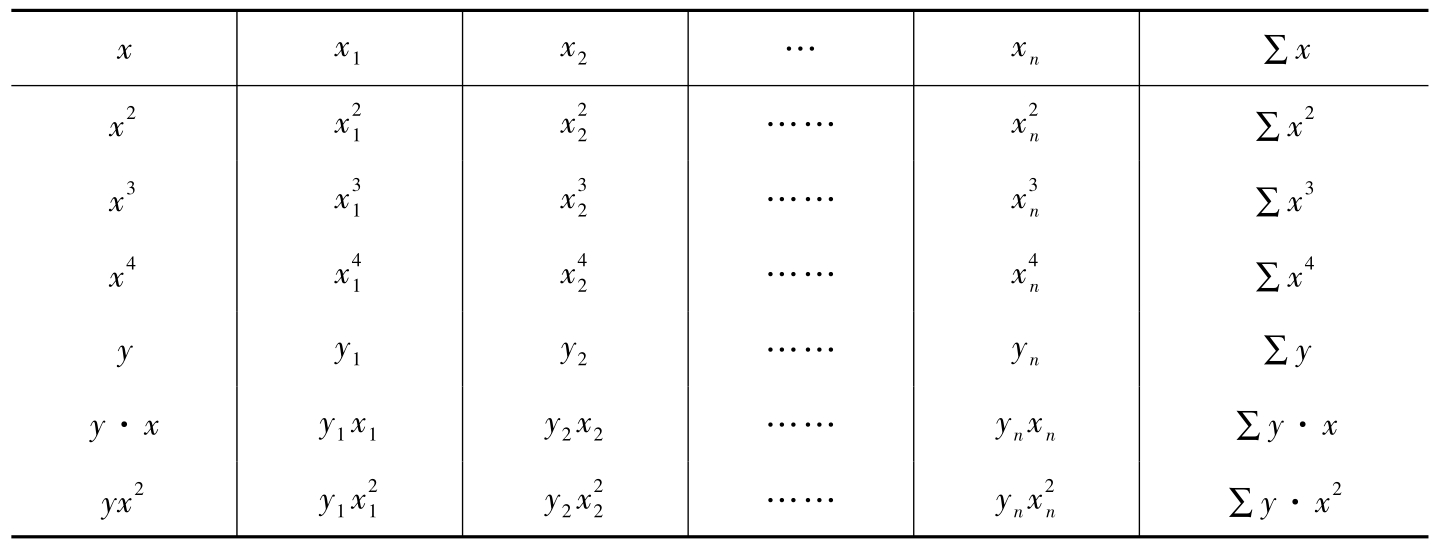
对应的数据计算表为表2-2。

表2－2　多元线性回归参数计算表

其计算较为复杂，最好能编成程序，由电子计算机操作。

2.指数曲线

当现象的环比发展速度（即后项与前项之比）大体相同时，可配置指数曲线方程：y=a·b^x。

求解参数a、b的方法如下：

对方程y=a·b^x取对数：

对应的方程组为：

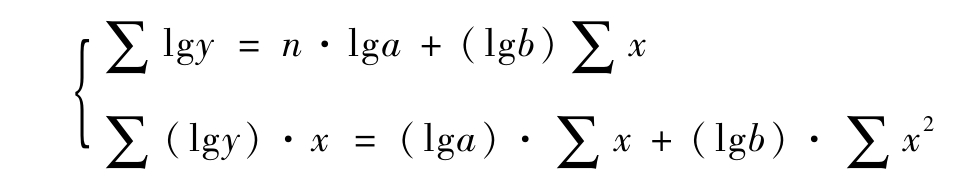
由该方程组可求得：lga，lgb，进而求得a、b；指数曲线方程y=a·b^x也就求出来了。

对应的数据计算表为表2-3。

表2－3　指数曲线参数计算表

（三）马尔柯夫链预测法

市场预测是马尔柯夫链的有效运用场合，它针对用户在不同厂家产品下相互转移的情况。

举例如下（表2-4）：

表2－4　甲、乙、丙三家矿山开发项目的矿石销售量表

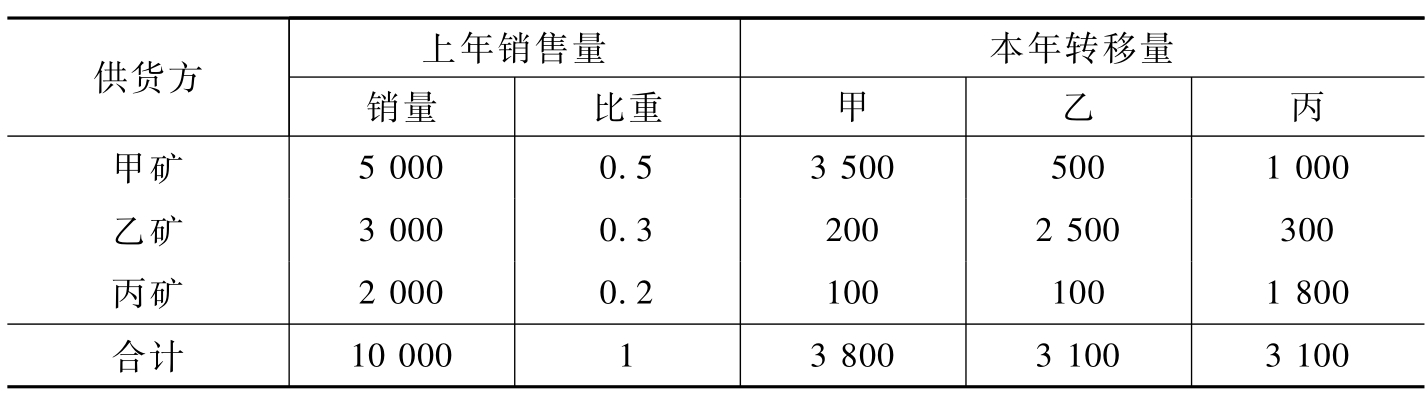
表2-4的含义为：最初（上年）甲、乙、丙三者有各自的市场销售量及其市场占有率，但是，用户可能在甲、乙、丙之间相互转移，也就是上期购买某家产品，今年转向购买另一家的产品。

依据表2-4的资料，甲、乙、丙之间相互转移的数据为：

甲向乙、丙转移：甲转乙为500／5000=1／10；甲转丙为1000／5000= 2／10；保留在甲为3500／5000=7／10；合计为1。

乙向甲、丙转移：乙转甲为200／3000=1／15；乙转丙为300／3000= 1／10；保留在乙为2500／3000=5／6；合计为1。

丙向甲、乙转移：丙转甲为100／2000=1／20；丙转乙为100／2000= 1／20；保留在丙为1800／2000=9／10；合计为1。

马尔柯夫链认为：只要用户转移比率稳定（也就是从第二年起，用户在上述三个厂家转移率不变），那么，若干年后，甲、乙、丙三方的市场占有率必然呈稳定状态。该稳定态下，甲、乙、丙的用户仍按上述比例相互转移，但各家的市场占有率就会保持不变（也就是出现了一种动态的稳定状态，各家当年转出的用户数量正好等于转入的用户数量，用户总量及对应的市场占有率保持不变）。

马尔柯夫链正是寻找这一稳定状态的最有效方法。

具体步骤如下：

（1）列出各厂家用户的转移概率矩阵：

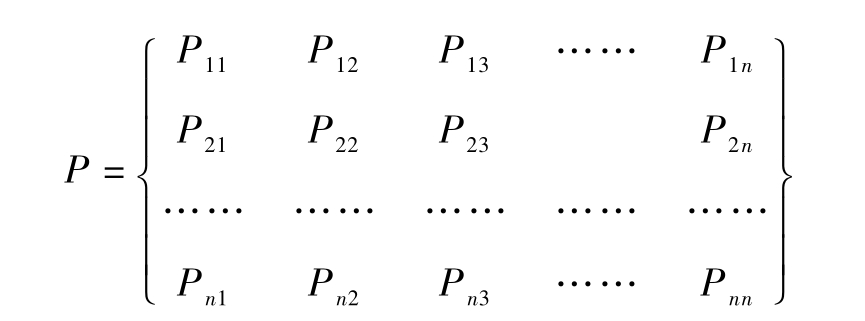
矩阵中：P_ij在0-1之间，每行的P合计为1。即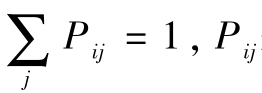表示第i家的用户向第j家转移的概率。

（2）找到各厂家最初的市场占有率：

式中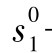，——表示初始市场上第一厂家的占有率；

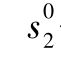——为第二厂家市场占有率，等等。

依上例就有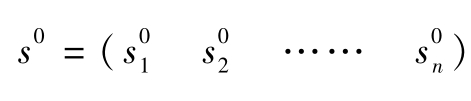：=（0.5，0.3，0.2），即上年各矿的市场占有率分别为：甲0.5，乙0.3，丙0.2，在某一市场上各厂家市场占有率合计为1。

（3）预测以后各期各厂家的市场占有率：

S^（k）=S^（0）·P^k

用具体的矩阵表示为：

只要具备起码的矩阵运算知识，上述马尔柯夫链的求解并不复杂。仍以上例，代入相应数字有：

一年后，各矿市场占有率为：

三年后各矿的市场占有率为：

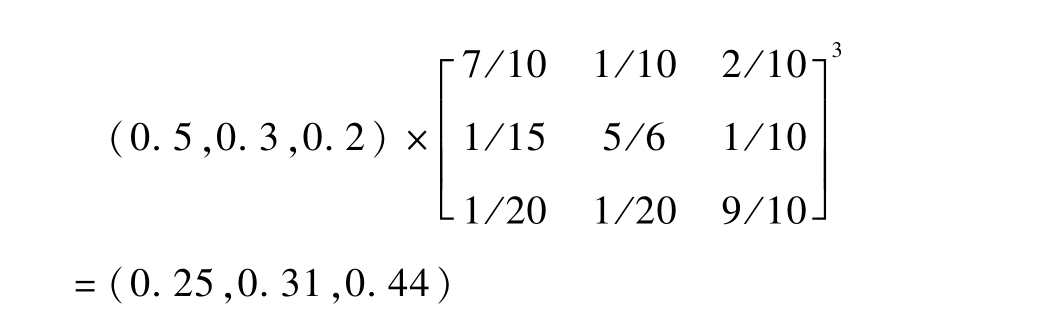
（4）求解稳定状态。稳定状态下，市场占有率不再变化，设为S^（K）就有：S^（k+1）=S^（k）·P=S^（k）

上式的含义为，到达稳定态后，该稳态不再随转移而改变。

即有：

S^（k）P-S^（k）=0或S^（k）（P-I）=0

式中P为转移概率矩阵，I为单位矩阵。

（P-I）是秩为n-l的非满秩矩阵，（P-I）的特征值λ=1。

由此可知，S^（k）有一系列的非零解。在众多的非零解中，各分量之和为1的那个解，正是我们所需要的结论。

设为：

S^（k）=（x₁　x₂……x_n）

满足下列条件：

从中可求得x₁，x₂……x_n，就是稳定状态下各厂家的市场占有率。仍以上例有：

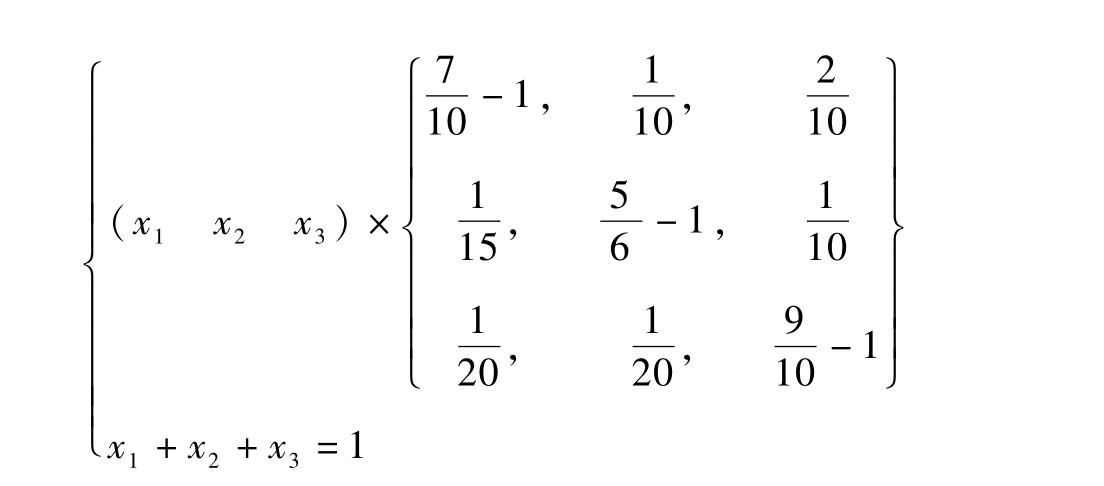
即：

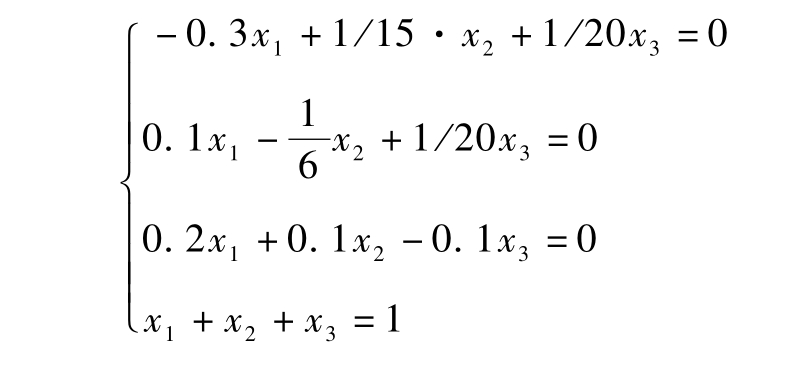
化简得：

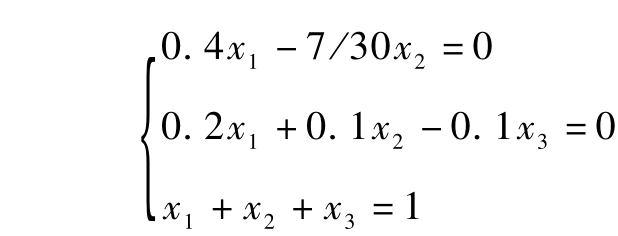
可以解得：

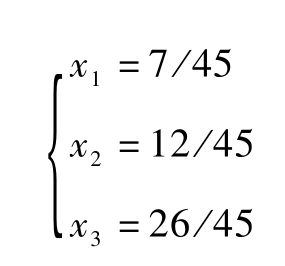
即：若干期后，虽然各用户仍按原概率矩阵转移，但是，甲、乙、丙三家的市场占有率稳定为：7／45，12／45，26／45。

（四）其他数学模型预测法

市场预测的数学模型还很多，如成长曲线法，最优分割法，博克斯-詹金斯预测法，多层递阶法，灰色系统法，等等。

这些方法在一定程度上已转化为纯粹的数学方法，但其预测的科学性及准确性都是相当高的。有兴趣的读者可参阅专门介绍有关市场预测方法的书籍，不难掌握。