计算实验结果分析

通过对j30-files、j60-files和j120-files三个测试集共1560个测试问题的计算实验，本书提出的求解PSM2模型的内环蚁群算法的平均求解时间为7.366秒。与前向／后向混合迭代算法的计算结果相比，最优目标函数值的平均改进率为12.526％；与Rand-50算法的计算结果相比，最优目标函数值的平均改进率为4.29％（如表3.10所示）。

表3.10　算法有效性实验的计算结果对比

为揭示影响算法有效性的深层次因素，需对计算结果进行分层分析。分层方案有按工序数和按资源强度两种情况。按工序数分层，计算结果如表3.11和图3.21所示。

由表3.11和图3.21可以看到，随着工序数的增加，算法的平均计算时间也相应增加。这主要是由于项目工序数的增加，算法产生一个可行解所需的计算量随之增加；加之随着工序数的增加，算法需要搜索的可行解的空间增大，从而使得算法的计算量增加。相对于Rand-50算法，随着工序数的增加，最优目标函数值的平均改进率也随之增加。这主要是因为随着工序数的增加，可行解空间随之增加，Rand-50算法产生的可行解占到整个可行解空间的比例减小，从而使得它搜索到相对较优的可行解的概率减小，同时，本书所提出的内环蚁群算法是按照某种全局最优的搜索策略搜索可行解空间，因此它相对不大受可行解空间大小的影响，所以本书提出的方法相对于Rand-50算法搜索到的最优解的目标函数值改进率会随着工序数的增加而增加。相对于前向／后向混合迭代算法，随着工序数的增加，最优目标函数值的改进率呈现先降后升的规律，对于工序数为60的测试实例，本书所提的内环蚁群算法的最优目标函数值改进率最小。这主要是由于前向／后向混合迭代算法并不像Rand-50算法那样随机地搜索可行解空间，而是按照某种启发式规则（现金流权重）进行搜索，因此它没有表现出Rand-50那样的最优目标函数值改进率变化规律。另一方面，工序数为120时最优目标函数值改进率最大的事实说明，前向／后向混合迭代算法所受到的可行解空间变化的影响要比本书所提的内环蚁群算法更大，因此在工序数较多时，本书提出的内环蚁群算法更适合于求解PSM2模型。

表3.11　不同工序数下的计算结果对比

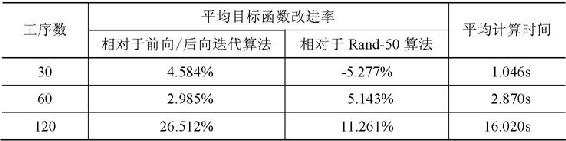
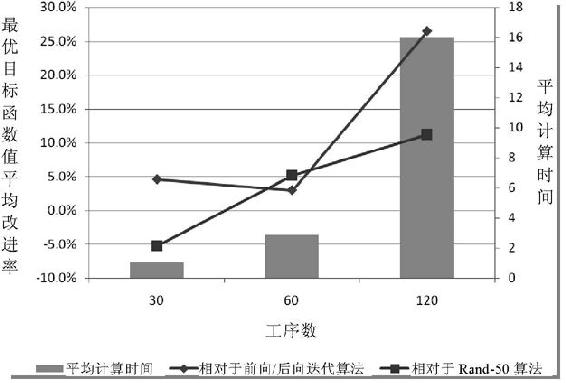
图3.21　不同工序数下的计算结果对比

按资源强度分层的计算结果如表3.12、图3.22所示。从中可以看到，随着资源强度的增加，计算时间基本上呈现递减的趋势。这是因为资源强度是一个表示资源“紧”的程度的指标，资源强度越大，说明资源约束对进度安排的影响越小。而可行解的产生是需要考虑资源约束的，资源约束越大，可行解产生所需的计算量也就越大。因此资源强度越大，算法所需的计算量越小，所需的计算时间也越小。

相对于前向／后向混合迭代算法，随着资源强度的增加，最优目标函数值的改进率基本上呈现递减的趋势。而当资源强度达到1时，即资源约束完全不影响项目的进度安排，最优目标函数值的改进率仅为0.006％。这说明对于资源不受限的情况，本书提出的内环蚁群算法和传统的启发式方法在求解性能上几乎没有差别，但对于资源受限的情况，本书提出的方法显然更具有竞争力。

表3.12　不同资源强度下的计算结果对比

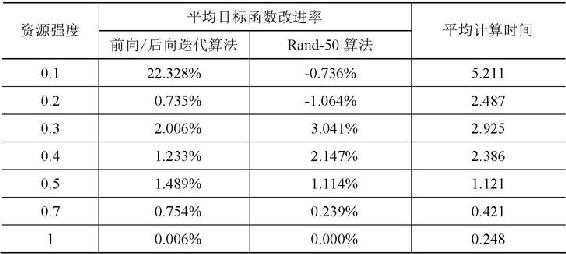
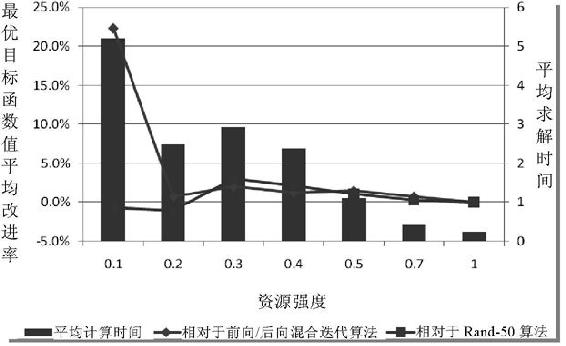
图3.22　不同资源强度下的计算结果对比

相对于Rand-50算法，随着资源强度的增加，最优目标函数值的改进率呈现先上升后下降的趋势。这说明对于资源约束很“紧”和很“松”两种情况，本书提出的内环蚁群算法和Rand-50算法在性能上差别不大，但对于资源约束在0.3—0.5这些情况，本书提出的内环蚁群算法显然具有更好的寻优性能。

综上所述，相对于前向／后向混合迭代算法和Rand-50算法，本书提出的内环蚁群算法在寻优能力上具有更好的性能，在寻优效率上能够满足工程实际的需要。而对于具有较多工序数和资源强度较“紧”的项目环境，本书提出的内环蚁群算法更适于求解PSM2模型。