股指期货套期保值基本模型

(一)　股指期货套期保值基本模型

套期保值比率h是指套期保值者在对现货进行套期保值时，用来计算所需买进或卖出某种期货合约数量的比率。测算h是套期保值成功的关键。

假设投资者在t时刻卖空价值N_F的股指期货合约，N_A为价值的现货资产进行套期保值。假设最优套保比率为h，持有的需保值资产(N_A)与在最优套保水平下进行套保资产(N_F)的关系可表示为:

最优套保合约数量(N^*)表示为:

其中Q_F表示股指期货合约规模。

综合国际研究结论，套期保值比率h可以通过以下方法计算:

1.普通最小二乘法(OLS)模型

根据最小方差(MV)模型的原理，假设现货与期货的头寸分别为C_S与C_F，则投资组合的收益率R_P可以表示为:

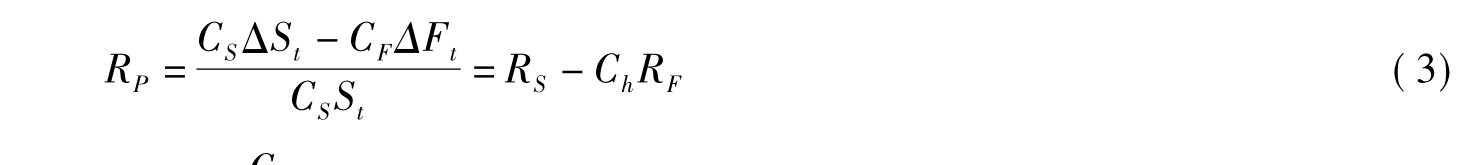
上式中C_h=C_F

C

S为套期保值比率。

对投资组合的收益率求取方差，可以得到

Var(R_P)=Var(R_S)-2hCov(R_S，R_F)+h²Var(R_F)(4)

由一阶条件最优套期保值比率的解析式为:

σ

F(5)

这也是动态套期保值头寸的定义表达式。其中，σ_S，σ_F和ρ分别表示现货与期货收益率的标准差，及二者的相关系数。

在MV模型的实现过程中，经常使用OLS方法。OLS方法是建立在历史数据的基础上，用已有的时间序列数据进行分析，从而使得回归分析的结果更能说明现货与期货价格之间的关系。

ΔS_t=α+βΔF_t+ε_t(6)

其中ΔS_t、ΔF_t分别表示采用套期保值的现货和期货的对数收益率。通过普通最小二乘法(OLS)估计线性模型的斜率β，该斜率即是套期保值比率。

2.向量自回归(VAR)模型

向量自回归(VAR)模型可以克服OLS模型残差序列自相关的缺点。对现货和期货价格的对数收益率建立二元VAR(Bivariate-VAR)模型如下:

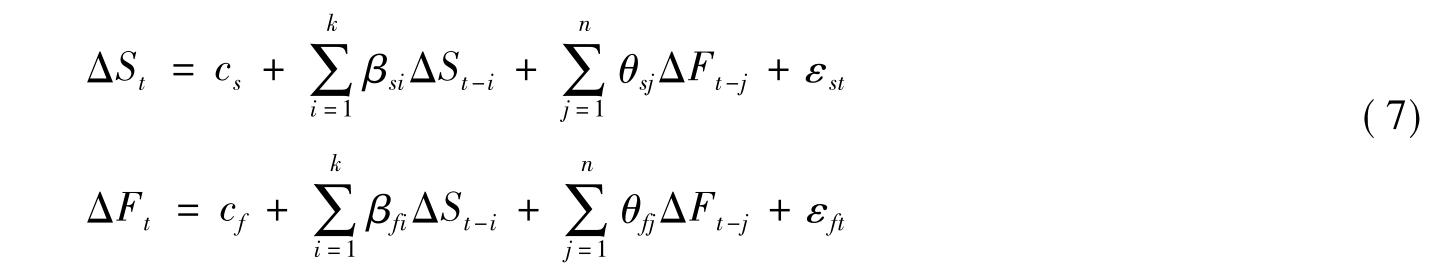
其中ΔS、ΔF分别代表现货、期货的对数收益率，c为常数项，β和θ分别为系数。随机向误差向量ε_st和ε_ft独立同分布，则h^*可表示为两者协方差与期货残差项ε_ft方差的比值:

3.向量误差修正模型(VECM)

在协整的概念基础上，利用ECM进行h^*的估算。同时考虑期货和现货价格的VECM模型可表示为:

Δs_t=c+αZ_t-1+βΔf_t+ε_t(9)

其中，c为常数项，α、β分别为变量系数。而Z_t-1=S_t-1-(a+bF_t-1)就是误差修正项。则h^*同样可以表示为:h^*=β。

4.ECM-BGARCH模型

金融资产收益率的当期条件异方差不仅受到前期残差的影响，也受到前期条件异方差的影响。我们常用ARCH过程或GARCH过程来描述这种关系。ECMBGARCH模型的均值方程设定如下:

Δs_t=α_s+β_sZ_t-1+ε_s，t-1(10)

Δf_t=α_f+β_fZ_t-1+ε_f，t-1(11)

此处的均值方程中包含的Z_t-1=S_t-1-(a+bF_t-1)就是误差修正项。ECMBGARCH模型的方差方程设定如下:

Vec(H_t)=C+A·Vec(ε_t-1ε^T

t-1)+B·H_t(12)

其中，C为3×1的参数向量;C和C为3×1的系数矩阵。同时为了简化参数估计，假定残差项ε_s，t和ε_f，t之间的相关系数为常数ρ_sf。此时

vec算子取矩阵“上三角形”部分，把每一元素排成一个单列向量，例如:vec(H_t)= h_ss，t h_ff，t h_sf，t(14)

把上述矩阵形式表示的条件方差方程展开可得到:

这时我们可以知道最优套保比率