公司市场价值和负债比例正相关

二、MM资本结构理论

MM资本结构理论的发展分为三个阶段：（1）1958年6月，MM无公司税资本结构理论，又称资本结构无关理论。1958年6月，莫迪哥莱尼（Franco Modigliani）教授与米勒（Merton H.Miller）教授在《美国经济评论》杂志上发表的《资本成本、公司理财与投资理论》（The Cost of Capital，Corporation Finance and the Theory of Investment）一文，阐释了这一理论。MM在严格的假设前提之下，以无套利分析技术论证了资本结构与公司价值之间的不相关关系。（2）1963年6月，MM有公司税资本结构理论。1963年6月，MM两教授在《美国经济评论》杂志上发表了《公司所得税与资本成本》（Corporate Income Taxes and the Cost of Capital）一文，探讨了在有公司所得税的情况下，资本结构是如何影响公司价值的。（3）1977年5月，米勒模型。1977年5月，米勒教授在《金融杂志》上发表了一篇论文《债务与税》（Debt and Taxes），认为MM有公司税资本结构理论夸大了公司所得税对于公司价值的正向作用。同时，私人所得税的存在会抵消这种影响。尤为重要的是，在米勒均衡状态下，即使存在着各种所得税，资本结构对公司价值也没有影响。米勒模型是MM资本结构理论的一般形式，其他两种理论均可由此导出。

MM无公司税模型建立在以下假设的基础上：

1.公司经营风险可由纳税付息前利润的标准差（δ_EBIT）来衡量，有相同经营风险的公司处于同类风险级。

2.现在或潜在的投资者对每一个公司未来的纳税付息前利润的估计完全相同，即投资者对公司未来的收益和风险的预期是相同的。

3.股票和债券在完全资本市场上交易意味着：没有交易成本，投资者（个人和组织）可与公司一样以同等利率借款。

4.公司和个人的负债没有风险，负债利率为无风险利率。此外，无论公司或个人举债多少，这个假设不变。

5.所有现金流量都是固定年金，即公司的增长率为0。

MM无公司税模型包括如下三个命题：

命题一，公司价值命题

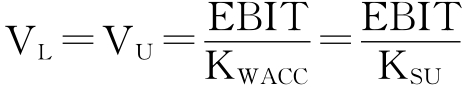
命题二，风险补偿命题

K_SL＝K_SU＋（K_SU－K_d）（D/S）

命题三，投资报酬率命题

IRR≥K_d＝K_SU

式中：EBIT为纳税付息前利润；K_WACC为加权平均资本成本；K_SU为处于一定风险等级中的资金来源全部为股权资本的投资者期望报酬率；K_d为负债利率；D为负债市场价值；S为股票市场价值；IRR为内含报酬率；L为有负债公司；U为无负债公司即全部股权资本公司。

命题一说明，只要EBIT相等，那么处于同一风险等级里的公司，无论是负债经营的公司还是无负债经营的公司（全为股权资本经营的公司），它们的价值相等。公司的资本结构与公司的加权平均资本成本、公司价值毫不相关。命题二是对命题一的进一步阐述。在MM的世界里，之所以资本结构对资本成本、公司价值不产生影响，是因为负债率的提高在降低加权平均资本成本的同时，又会由于风险的加大而使得股权资本成本提高，即所谓的风险补偿，（K_SU－K_d）（D/S）。负债率（D/S）越高，负债因素使得加权平均资本成本降低越多，但股权资本的风险补偿也会越多，这又会提高加权平均资本成本的水平。两者相互抵消，使得公司的加权平均资本成本的水平始终与无负债状态下的股权资本成本相同，即K_WACC＝K_SU。命题三说明，内含报酬率大于加权平均资本成本或者预期报酬率是进行资本预算决策的基本前提。只有采纳了内含报酬率大于加权平均资本成本即净现值大于0的项目，公司价值才能够得以增加。在有效的资本市场上，公司股票的行市也会因此而提高。

MM两教授运用无套利证明的方法论证了他们的资本结构命题。

例如，有风险相同的A、B两家公司。除了A公司完全没有负债，而B公司有60000元、利率为5%的债务之外，其他各方面均相同。依据一般的思路，由于B公司采用了成本较低的负债作为资金的来源，会通过降低加权平均资本成本来提高公司的价值。因而，B公司的价值应当高于A公司的价值，即V_A＜V_B。

但MM认为，这种认识是错误的。B公司的价值被高估了，而且这种情形无法继续下去，因为套利行为会使得两个公司的价值最终趋于相等。理性的投资者即套利者会出售被高估公司的股票，购买被低估公司的股票，这个过程将会一直持续到两个公司的市场价值完全相等为止。B公司的投资者可以投资于A公司而得到相同金额的报酬，同时，在无需增加融资风险的情况下，还能以较低的支出得出上述的结果。由于投资者可以通过支出较少的投资来增加财富，因此，B公司的投资者将出售其所持有的B公司的股票，购买A公司的股票。此种套利行为将一直持续下去，直到B公司股票价格下跌，同时，A公司股票价格上扬至两家公司的价值完全相等，即V_A＝V_B为止。

在套利过程中，市场上必须有理性的投资者（套利者），他无视公司财务杠杆与个人财务杠杆的差异，且资本市场是完全有效的，没有交易成本，没有破产、代理成本等。而这一切在事实上却做不到。所以，MM的最初资本结构理论是在极端假设条件下建立的一个具有极端性质的资本结构模型。这一理论的重要意义在于它揭示了负债运用的收益与成本之间的密切相关性，形成了第一个科学的、严谨的资本结构理论，并以此推动了整个财务理论的发展。

1963年，MM两教授在以往研究的基础上加入了公司所得税因素，发展了他们的资本结构理论。

MM有公司税资本结构理论同样包括三个命题：

命题一，公司价值命题

V_L＝V_U＋TD

命题二，风险补偿命题

K_SL＝K_SU＋（K_SU－K_d）（1－T）（D/S）

命题三，投资报酬率命题

IRR≥K_SU［1－T（D/V）］

MM有公司税模型的中心思想是：由于利息的支付是可以抵税的，因此财务杠杆降低了公司税后的加权平均资本成本，进而提高了公司价值。

例如，有A、B两家公司，A公司为全股权资本经营公司，没有负债，B公司有8000元、利率为5%的公司债，公司所得税税率为50%，其他资料均相同，详见表6－6。

表6－6　　　　　　　单位：万元

续表

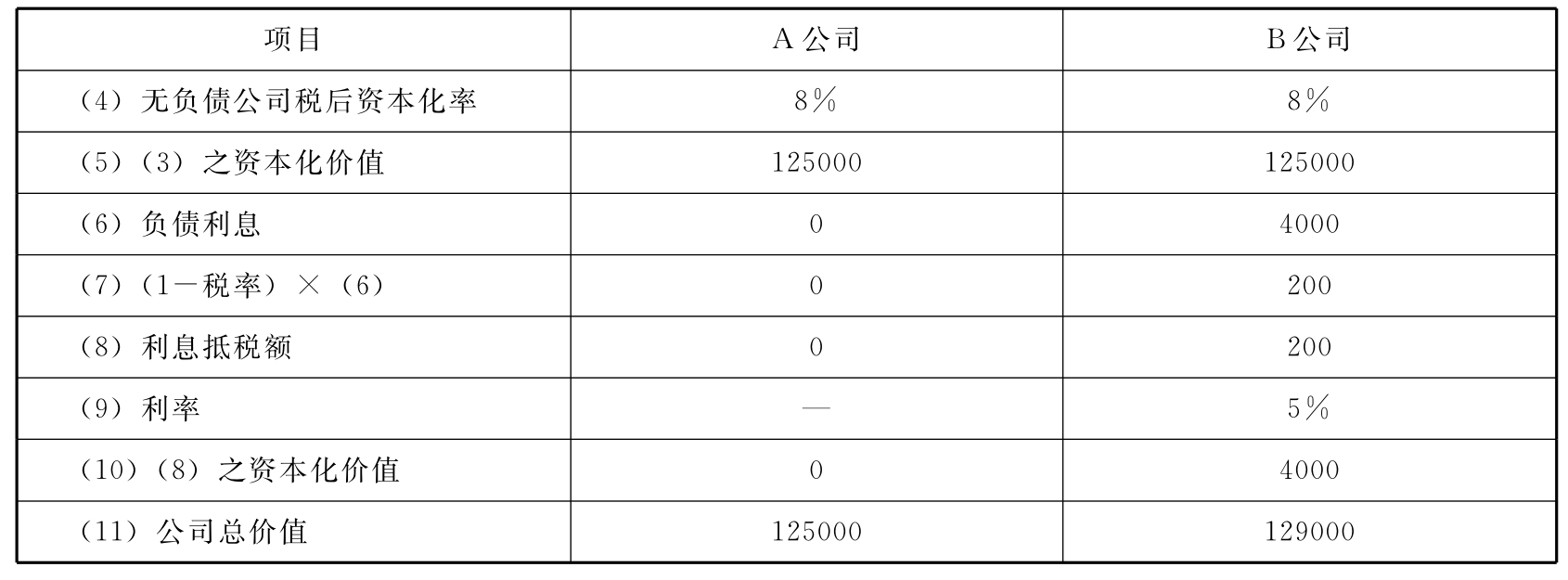
表6－6中第5项为股权资本价值，即息前税后净利之资本化价值；第10项为负债价值，即利息抵税额之资本化价值。依照MM理论，当公司所得税存在时，这两项之和即为公司总价值。公司总价值亦可用以下公式直接计算求得：

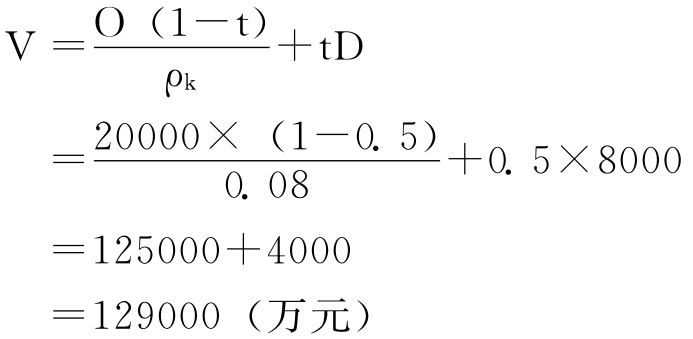
式中：O为预期营业净利；t为所得税税率；ρk为某一风险等级下无负债公司的税后资本化率（普通股东要求报酬率）；D为负债市场价值。

上式表明，一公司的价值会随着所使用负债的增加而增加。就某种意义上讲，政府补贴使用负债的公司，负债越多，政府给予公司的补贴越多，因而增加了公司价值。

同时，在不考虑财务风险的情况下，使用负债越多，公司的加权平均资本成本就越低。经税负调整后的资本成本为：

总之，按照有公司税的MM资本结构理论，一公司可经由财务杠杆的不断提高而持续不断地降低其资本成本，增加公司价值。财务杠杆程度越高，资本成本越低，公司价值就越大。100%的负债率是使公司价值达到最大的负债率水平。

米勒教授显然也意识到了以上结论的谬误之处，因此沿着以上研究的轨迹进一步发展和完善了MM资本结构理论，这就是关于资本结构的米勒模型的提出。

米勒教授认为，有公司税的资本结构模型夸大了利息由于抵税给公司价值所带来的增值作用。作为公司价值的最终享有者，普通股股东的收益水平不仅仅涉及公司所得税，还会涉及个人所得税的多寡。具体言之，较低的公司所得税支付，可能由于税法的原因，会带来较多的个人所得税支付，从而抵减了公司所得税所带来的优势。而恰恰是个人所得税的存在在很大程度上抵消了公司所得税对于公司价值的正向影响。

假设T_c为公司所得税税率，T_s为适用于股票所得（含股利与资本利得）的个人所得税税率，T_d为适用于利息所得的个人所得税税率。

考虑到个人所得税因素，无负债公司的价值可表述为：

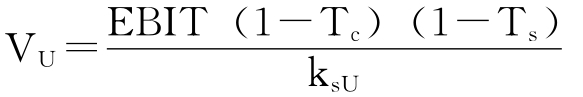
由于个人所得税的加入，事实上是减少了可以支付给投资者的收益。

米勒模型同样可以用无套利证明的方式来予以论证。下面的论证方法更为简单。首先将有负债公司的现金流量CF_L划分为属于股东所有的现金流量与属于债权人所有的现金流量两部分：

CF＝属于股东所有的现金流量＋属于债权人所有的现金流量

＝（EBIT－I）（1－T_c）（1－T_s）＋I（1－T_d）

上式中I为利息。上式可进一步调整为：

CF_L＝［EBIT（1－T_c）（1－T_s）］－［I（1－T_c）（1－T_s）］＋［I（1－T_d）］

上式中的第一项为无负债公司的税后现金流量，对其进行折现的折现率应当是k_sU。第二项与第三项均为与财务杠杆相关的现金流量，对其进行折现的折现率是负债的成本，即k_d。将以上三项现金流量的现值相加，即可得有负债公司的价值，如下：

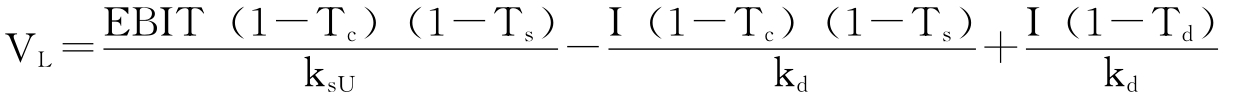
上式中的第一项即为无负债公司的价值，因此：

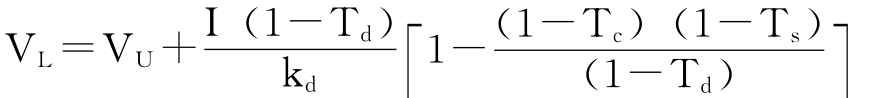
税后的、永续的利息除以债权人的要求报酬率即是债务的市场价值（D），即：

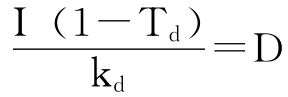
所以，

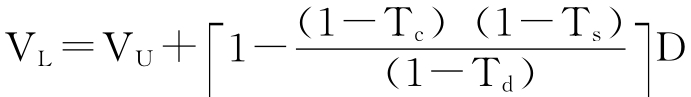
这就是著名的米勒模型（Miller Model）。

对米勒模型可做如下说明：

1.来自于财务杠杆的收益为：

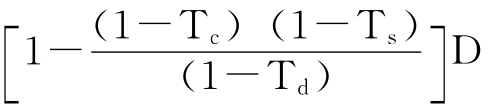
这取代了MM无公司税模型中的TD。

2.如果舍去各种所得税因素，即T_c＝T_s＝T_d＝0，则米勒模型回到最初的MM无公司税资本结构模型。

3.如果舍去个人所得税因素，即T_s＝T_d＝0，则中括号内［1－（1－T_c）］减少为T_c。米勒模型回到有公司税的MM资本结构模型。

4.如果适用于股票收益的所得税税率等于适用于债务收益的所得税税率，即T_s＝T_d，则（1－T_s）与（1－T_d）可以抵消，同样回到有公司税的MM资本结构模型。

5.如果（1－T_c）（1－T_s）＝（1－T_d），即债务对公司价值的抵税优势恰好被个人所得税在股票收益上的优势所抵消，则使用财务杠杆给公司价值带来的影响为0，资本结构与公司价值无关。米勒模型回到了无公司税的MM资本结构模型。

6.由于股票收益适用的所得税税率较低，且可以递延，因此，股票收益税率通常要低于债务收益税率。在这种情况下，来自于财务杠杆的收益要低于在MM无公司税资本结构模型下所计算的水平。假设T_c＝40%，T_d＝30%，T_s＝20%，则有负债公司的价值要比无负债公司的价值增加所运用负债的市场价值的31%：

按照有公司税的MM资本结构模型，来自于财务杠杆的收益相当于公司所运用负债的市场价值的40%，即T_cD＝0.40D，大于米勒模型下的0.31D。换言之，早期的MM资本结构理论高估了财务杠杆对于公司价值的增值作用。

在米勒模型中，还有一个问题必须再做说明，即米勒均衡状态。如果（1－T_c）（1－T_s）＝（1－T_d），就意味着实现了米勒均衡。在这种状态下，资本结构的任何变化同样不能作用于公司价值。这可以看成是对MM无公司税资本结构理论的另一种证明。